Giải bài 102 trang 43 sách bài tập toán 12 - Cánh diều
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số bậc ba (y = fleft( x right) = a{x^3} + b{x^2} + cx + d) có đồ thị là đường cong như Hình 30. a) Phương trình (fleft( x right) = 4) có hai nghiệm (x = - 1,x = 2). b) Phương trình (fleft( x right) = - 1) có hai nghiệm. c) Phương trình (fleft( x right) = 2) có ba nghiệm. d) Phương trình (fleft( {fleft( x right)} right) = 4) có sáu nghiệm.
Tổng hợp đề thi giữa kì 2 lớp 12 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
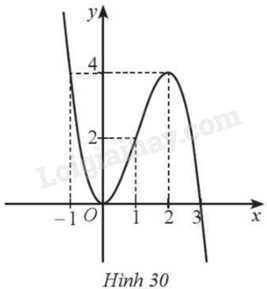
Cho hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong như Hình 30.
a) Phương trình \(f\left( x \right) = 4\) có hai nghiệm \(x = - 1,x = 2\).
b) Phương trình \(f\left( x \right) = - 1\) có hai nghiệm.
c) Phương trình \(f\left( x \right) = 2\) có ba nghiệm.
d) Phương trình \(f\left( {f\left( x \right)} \right) = 4\) có sáu nghiệm.
Phương pháp giải - Xem chi tiết
‒ Xét đồ thị hàm số.
Lời giải chi tiết
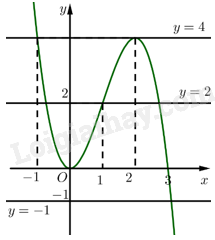
• Đường thẳng \(y = 4\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm có hoành độ bằng ‒1 và 2 nên phương trình \(f\left( x \right) = 4\) có hai nghiệm \(x = - 1,x = 2\). Vậy a) đúng.
• Đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại một điểm nên phương trình \(f\left( x \right) = - 1\) có một nghiệm. Vậy b) sai.
Đường thẳng \(y = 2\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại ba điểm nên phương trình \(f\left( x \right) = 2\) có ba nghiệm. Vậy c) đúng.
• Ta có: \(f\left( {f\left( x \right)} \right) = 4\) khi \(f\left( x \right) = - 1\) hoặc \(f\left( x \right) = 2\).
Với \(f\left( x \right) = - 1\), phương trình có một nghiệm.
Với \(f\left( x \right) = 2\), phương trình có ba nghiệm phân biệt. Vậy phương trình đã cho có bốn nghiệm phân biệt. Vậy d) sai.
a) Đ.
b) S.
c) Đ.
d) S.













Danh sách bình luận