Bài 4. Tổng và hiệu của hai vecto Toán 10 Cánh diều

Lý thuyết Tổng và hiệu của hai vecto - SGK Toán 10 Cánh diều

A. Lý thuyết 1. Tổng của hai vecto a) Định nghĩa

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

A. Lý thuyết

1. Tổng của hai vecto

a) Định nghĩa

Với ba điểm bất kì A, B, C, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \), kí hiệu là \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \).

Phép lấy tổng của hai vecto còn được gọi là phép cộng vecto.

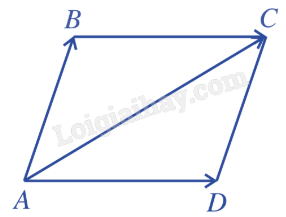
b) Quy tắc hình bình hành

Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).

c) Tính chất

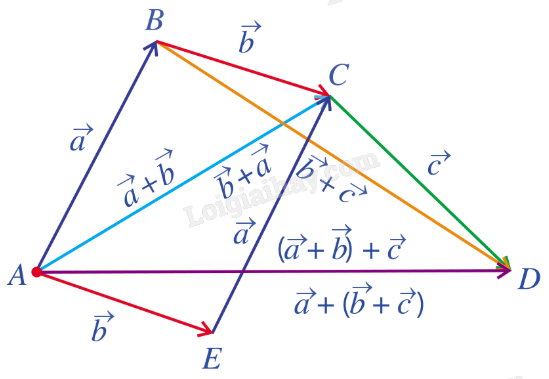
Với ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) tùy ý ta có:

- Tính chất giao hoán: \(\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)

- Tính chất kết hợp: \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)

- Tính chất của vecto-không: \(\overrightarrow a + \overrightarrow 0 = \overrightarrow a \)

2. Hiệu của hai vecto

a) Hai vecto đối nhau

Vecto có cùng độ dài và ngược hướng với vecto \(\overrightarrow a \) được gọi là vecto đối của vecto \(\overrightarrow a \), kí hiệu là \( - \overrightarrow a \). Hai vecto \(\overrightarrow a \) và \( - \overrightarrow a \) được gọi là hai vecto đối nhau.

Quy ước: Vecto đối của vecto \(\overrightarrow 0 \) là vecto \(\overrightarrow 0 \).

Nhận xét:

+) \(\overrightarrow a + ( - \overrightarrow a ) = ( - \overrightarrow a ) + \overrightarrow a \).

+) Hai vecto \(\overrightarrow a \), \(\overrightarrow b \) là hai vecto đối nhau khi và chỉ khi \(\overrightarrow a + \overrightarrow b = \overrightarrow 0 \).

+) Với hai điểm A, B, ta có: \(\overrightarrow {AB} + \overrightarrow {BA} = \overrightarrow 0 \).

Cho hai điểm A, B. Khi đó, hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BA} \) là hai vecto đối nhau, tức là \(\overrightarrow {BA} = - \overrightarrow {AB} \).

Chú ý:

+) I là trung điểm của đoạn thẳng AB khi và chỉ khi \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \).

+) G là trọng tâm tam giác ABC khi và chỉ khi \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).

b) Hiệu của hai vecto

Hiệu của vecto \(\overrightarrow a \) và vecto \(\overrightarrow b \) là tổng của vecto \(\overrightarrow a \) và vecto đối của vecto \(\overrightarrow b \), kí hiệu là \(\overrightarrow a - \overrightarrow b \).

Phép lấy hiệu của hai vecto được gọi là phép trừ vecto.

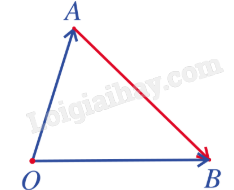
Nhận xét: Với ba điểm A, B, O bất kì, ta có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \).

B. Bài tập

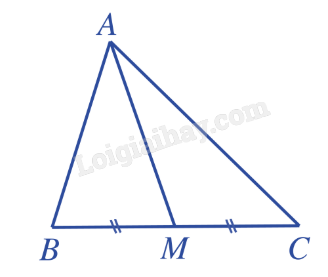
Bài 1: Cho tam giác ABC có trung tuyến AM. Chứng minh \(\overrightarrow {AB} + \overrightarrow {MC} = \overrightarrow {AM} \).

Giải:

Vì \(\overrightarrow {MC} = \overrightarrow {BM} \) nên \(\overrightarrow {AB} + \overrightarrow {MC} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AM} \).

Bài 2: Cho hình chữ nhật ABCD. Chứng minh \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {BA} + \overrightarrow {BC} } \right|\).

Giải:

Theo quy tắc hình bình hành, ta có:

\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \), \(\overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD} \).

Suy ra \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC\), \(\left| {\overrightarrow {BA} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {BD} } \right| = BD\).

Do AC = BD nên \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {BA} + \overrightarrow {BC} } \right|\).

Bài 3: Cho bốn điểm A, B, C, D. Chứng minh \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} = \overrightarrow {AD} \).

Giải:

Ta có \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} \)

\( = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} \) (tính chất giao hoán)

\( = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} \) (tính chất kết hợp)

\( = \overrightarrow {AC} + \overrightarrow {CD} \) (quy tắc ba điểm)

\( = \overrightarrow {AD} \) (quy tắc ba điểm).

Bài 4: Cho bốn điểm bất kì A, B, C, D. Chứng minh \(\overrightarrow {AB} - \overrightarrow {AD} + \overrightarrow {CD} - \overrightarrow {CB} = \overrightarrow 0 \).

Giải:

Ta có \(\overrightarrow {AB} - \overrightarrow {AD} + \overrightarrow {CD} - \overrightarrow {CB} = \left( {\overrightarrow {AB} - \overrightarrow {AD} } \right) + \left( {\overrightarrow {CD} - \overrightarrow {CB} } \right) = \overrightarrow {DB} + \overrightarrow {BD} = \overrightarrow {DD} = \overrightarrow 0 \).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục I trang 83, 84, 85 SGK Toán 10 tập 1 - Cánh diều
Một vât dịch chuyển từ A đến B và tiếp tục dịch chuyển từ B đến C (Hình 49). Cho ABCD là hình bình hành (Hình 52). So sánh: Hãy giải thích hướng đi của thuyền ở Hình 48.
Giải mục II trang 85, 86 SGK Toán 10 tập 1 - Cánh diều
Trong Hình 54, hai ròng rọc có trục quay nằm ngang và song song với nhau, hai vật có trọng lượng bằng nahu. Mỗi dây có một đầu buộc vào vật, một đầu buộc vào một mảnh nhựa cứng. Cho tam giác ABC có M là trung điểm AC, N là trung điểm BC và AB = a. Tính độ dài vecto
Giải bài 1 trang 87 SGK Toán 10 tập 1 – Cánh diều
Cho ba điểm M, N, P. Vecto
Giải bài 2 trang 87 SGK Toán 10 tập 1 – Cánh diều
Cho ba điểm D, E, G. Vecto
Giải bài 3 trang 87 SGK Toán 10 tập 1 – Cánh diều
Cho bốn điểm A, B, C, D. Chứng minh:
Giải bài 4 trang 87 SGK Toán 10 tập 1 – Cánh diều
Cho hình hình hành ABCD, gọi O là giao điểm của AC và BD. Các khảng định sau đúng hay sai?
Giải bài 5 trang 87 SGK Toán 10 tập 1 – Cánh diều
Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn.
Giải bài 6 trang 87 SGK Toán 10 tập 1 – Cánh diều
Cho ABCD là hình bình hành. Chứng minh
Giải bài 7 trang 87 SGK Toán 10 tập 1 – Cánh diều
Cho hình vuông ABCD có cạnh a. Tính độ dài các vecto sau:
Giải bài 8 trang 87 SGK Toán 10 tập 1 – Cánh diều
Cho ba lực F1=OA ;F2 = OB và F3=OC cùng tác động vào một vật tại điểm O và vật đứng yên.
Giải bài 9 trang 87 SGK Toán 10 tập 1 – Cánh diều
Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc là 10 km/h. Một chiếc ca nô chuyển động từ phía đông sang phía tây với vận tốc 40 km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông.