Lý thuyết Hàm số và đồ thị - SGK Toán 10 CTST

1. Hàm số. Tập xác định và tập giá trị của hàm số 2. Đồ thị hàm số 3. Hàm số đồng biến, hàm số nghịch biến

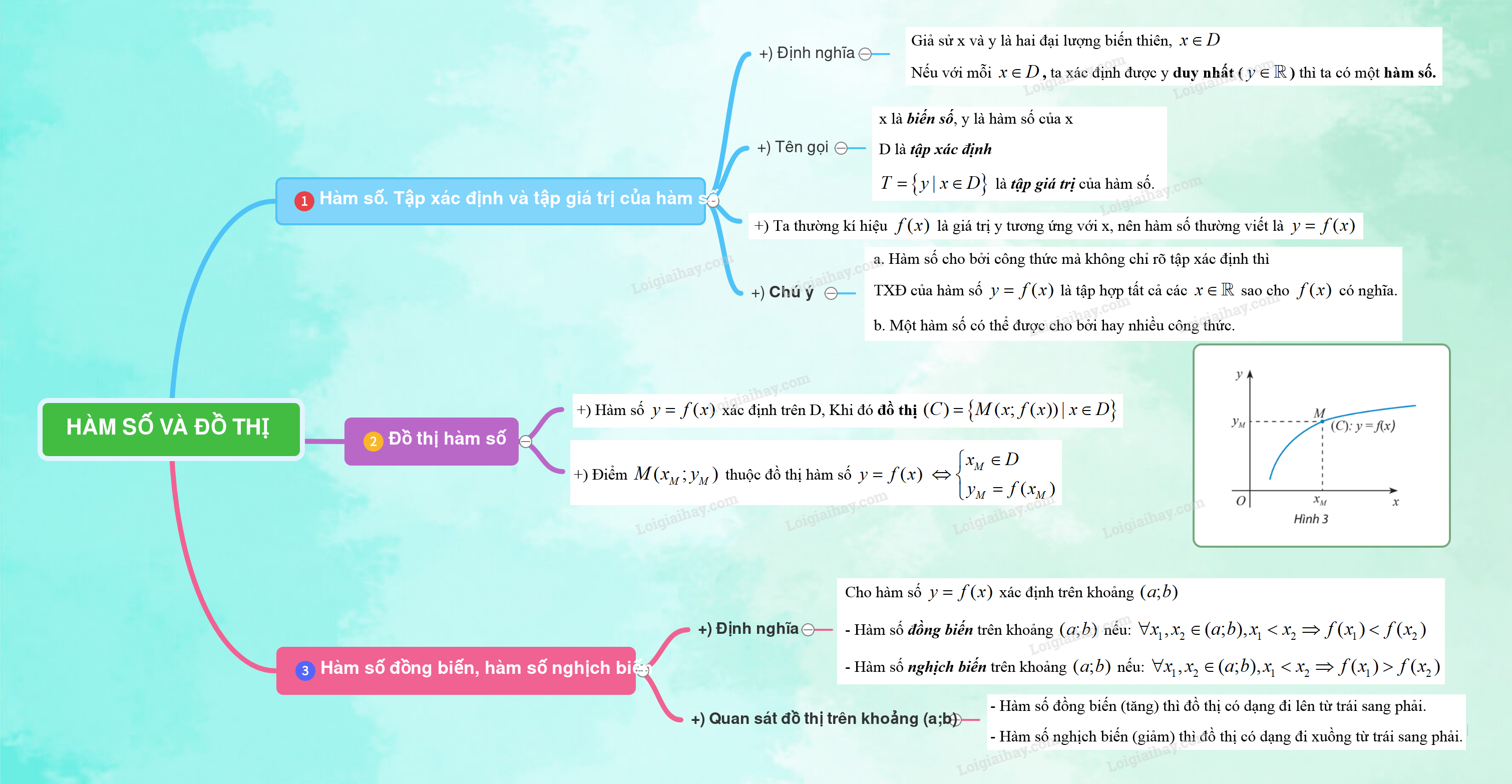
1. Hàm số. Tập xác định và tập giá trị của hàm số

+) Định nghĩa:

Giả sử x và y là hai đại lượng biến thiên, \(x \in D\)

Nếu với mỗi \(x \in D\), ta xác định được y duy nhất (\(y \in \mathbb{R}\)) thì ta có một hàm số.

+) Tên gọi:

x là biến số, y là hàm số của x

D là tập xác định

\(T = \left\{ {y|x \in D} \right\}\) là tập giá trị của hàm số.

+) Ta thường kí hiệu \(f(x)\) là giá trị y tương ứng với x, nên hàm số thường viết là \(y = f(x)\)

* Chú ý

a. Hàm số cho bởi công thức mà không chỉ rõ tập xác định thì

TXĐ của hàm số \(y = f(x)\) là tập hợp tất cả các \(x \in \mathbb{R}\) sao cho \(f(x)\) có nghĩa.

b. Một hàm số có thể được cho bởi hay nhiều công thức.

2. Đồ thị hàm số

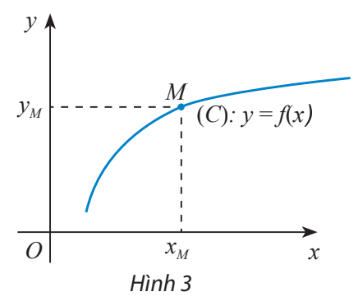
+) Hàm số \(y = f(x)\) xác định trên D, Khi đó đồ thị \((C) = \left\{ {M(x;f(x))|x \in D} \right\}\)

+) Điểm \(M({x_M};{y_M})\) thuộc đồ thị hàm số \(y = f(x)\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_M} \in D\\{y_M} = f({x_M})\end{array} \right.\)

3. Hàm số đồng biến, hàm số nghịch biến

+) Định nghĩa: Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\)

- Hàm số đồng biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)

- Hàm số nghịch biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)

+) Quan sát đồ thị: trên khoảng \((a;b)\)

- Hàm số đồng biến (tăng) thì đồ thị có dạng đi lên từ trái sang phải.

- Hàm số nghịch biến (giảm) thì đồ thị có dạng đi xuồng từ trái sang phải.

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 9 phiếu

Bài tiếp theo

Giải mục 1 trang 41, 42, 43 SGK Toán 10 tập 1 - Chân trời sáng tạo
Bản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 01/5/2021 tại thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên. Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
Giải mục 2 trang 43, 44 SGK Toán 10 tập 1 - Chân trời sáng tạo
Xét hàm số y = f(x) cho bởi bảng sau: a) Tìm tập xác định D của hàm số trên. b) Trong mặt phẳng tọa độ Oxy, vẽ tất cả các điểm có tọa độ (x; y) với x thuộc D và y = f(x). Vẽ đồ thị hàm số f(x) = 3x + 8
Giải mục 3 trang 45, 46, 47 SGK Toán 10 tập 1 - Chân trời sáng tạo
Quan sát đồ thị hàm số y = f(x) = {x^2} rồi so sánh f(x1) và f(x2) (với x1 < x2) trong từng trường hợp sau: a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
Giải bài 1 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm tập xác định của các hàm số sau:
Giải bài 2 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10.
Giải bài 3 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
Giải bài 4 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo
Vẽ đồ thị hàm số f(x) = |x|
Giải bài 5 trang 48 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:
Giải bài 6 trang 48 SGK Toán 10 tập 1 – Chân trời sáng tạo
Một hãng taxi có bảng giá như sau: a) Xem số tiền đi taxi là một hàm số phụ thuộc số kilomet di chuyển, hãy viết công thức của các hàm số dựa trên thông tin từ bảng giá đã cho theo từng yêu cầu:
Giải bài 7 trang 48 SGK Toán 10 tập 1 – Chân trời sáng tạo
Số 2 đã trải qua một hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau: Bên trong HỘP ĐEN là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết iểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.