Bài 1. Hàm số và đồ thị Toán 10 Chân trời sáng tạo

Giải mục 3 trang 45, 46, 47 SGK Toán 10 tập 1 - Chân trời sáng tạo

Quan sát đồ thị hàm số y = f(x) = {x^2} rồi so sánh f(x1) và f(x2) (với x1 < x2) trong từng trường hợp sau: a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:

Lựa chọn câu để xem lời giải nhanh hơn

HĐ Khám phá 3

Quan sát đồ thị hàm số $y = f(x) = {x^2}$ rồi so sánh $f({x_1})$ và $f({x_2})$ (với ${x_1} < {x_2}$ ) trong từng trường hợp sau:

Phương pháp giải:

Trên tia Oy, giá trị nào gần gốc tọa độ hơn thì nhỏ hơn.

Lời giải chi tiết:

a) $f({x_1}) > f({x_2})$

b) $f({x_1}) < f({x_2})$

Thực hành 4

a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:

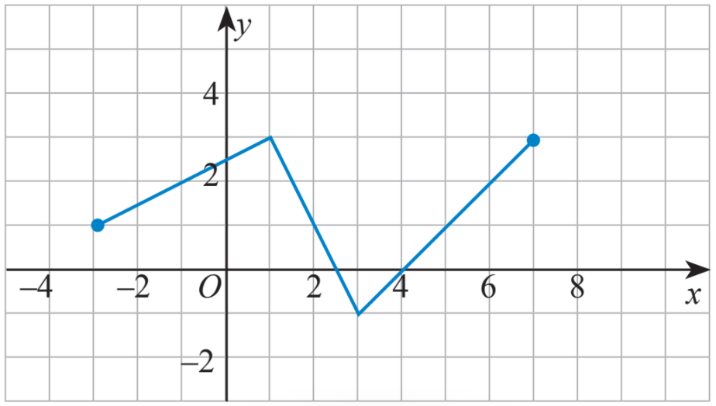
b) Xét tính đồng biến, nghịch biến của hàm số $y = f(x) = 5{x^2}$ trên khoảng (2; 5).

Phương pháp giải:

a) Quan sát đồ thị trên các khoảng (-3; 1), (1;3), (3;7)

Khi hàm số đồng biến trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải.

Khi hàm số nghịch biến trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.

Bước 1: Lấy ${x_1},{x_2} \in (2;5)$ là hai số tùy ý sao cho ${x_1} < {x_2}$ .

Bước 2: So sánh $f({x_1}) = 5{x_1}^2$ và $f({x_2}) = 5{x_2}^2$

Bước 3: Kết luận tính đồng biến, nghịch biến

+ Nếu $f({x_1}) < f({x_2})$ thì hàm số đồng biến trên khoảng (2; 5)

+ Nếu $f({x_1}) > f({x_2})$ thì hàm số nghịch biến trên khoảng (2; 5)

Lời giải chi tiết:

a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]

+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).

+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).

+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).

b) Xét hàm số $y = 5{x^2}$ trên khoảng (2; 5).

Lấy ${x_1},{x_2} \in (2;5)$ là hai số tùy ý sao cho ${x_1} < {x_2}$ .

Do ${x_1},{x_2} \in (2;5)$ và ${x_1} < {x_2}$ nên $0 < {x_1} < {x_2}$ , suy ra ${x_1}^2 < {x_2}^2$ hay $5{x_1}^2 < 5{x_2}^2$

Từ đây suy ra $f({x_1}) < f({x_2})$

Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).

Bình luận

Chia sẻ

Bình chọn:

4 trên 7 phiếu

Bài tiếp theo

Giải bài 1 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm tập xác định của các hàm số sau:
Giải bài 2 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10.
Giải bài 3 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
Giải bài 4 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo
Vẽ đồ thị hàm số f(x) = |x|
Giải bài 5 trang 48 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:
Giải bài 6 trang 48 SGK Toán 10 tập 1 – Chân trời sáng tạo
Một hãng taxi có bảng giá như sau: a) Xem số tiền đi taxi là một hàm số phụ thuộc số kilomet di chuyển, hãy viết công thức của các hàm số dựa trên thông tin từ bảng giá đã cho theo từng yêu cầu:
Giải bài 7 trang 48 SGK Toán 10 tập 1 – Chân trời sáng tạo
Số 2 đã trải qua một hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau: Bên trong HỘP ĐEN là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết iểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.
Giải mục 2 trang 43, 44 SGK Toán 10 tập 1 - Chân trời sáng tạo
Xét hàm số y = f(x) cho bởi bảng sau: a) Tìm tập xác định D của hàm số trên. b) Trong mặt phẳng tọa độ Oxy, vẽ tất cả các điểm có tọa độ (x; y) với x thuộc D và y = f(x). Vẽ đồ thị hàm số f(x) = 3x + 8
Giải mục 1 trang 41, 42, 43 SGK Toán 10 tập 1 - Chân trời sáng tạo
Bản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 01/5/2021 tại thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên. Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
Lý thuyết Hàm số và đồ thị - SGK Toán 10 CTST
1. Hàm số. Tập xác định và tập giá trị của hàm số 2. Đồ thị hàm số 3. Hàm số đồng biến, hàm số nghịch biến

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.