-
GIẢI SGK TOÁN 11 KẾT NỐI TRI THỨC VỚI CUỘC SỐNG - MỚI NHẤT
-
Toán 10 tập 1 - Kết nối tri thức với cuộc sống
-
Toán 10 tập 2 - Kết nối tri thức với cuộc sống
Lý thuyết Hàm số - SGK Toán 10 Kết nối tri thức
A. Lý thuyết 1. Khái niệm hàm số
A. Lý thuyết
1. Khái niệm hàm số
|
Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực ℝ thì ta có một hàm số. Ta gọi x là biến số và y là hàm số của x. Tập hợp D gọi là tập xác định của hàm số. Tập hợp tất cả các giá trị y nhận được, gọi là tập giá trị của hàm số. |
Khi y là hàm số của x, ta có thể viết y = f(x), y = g(x),…
Chú ý: Khi cho hàm số bằng công thức y = f(x) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
Nhận xét: Một hàm số có thể được cho bằng bảng, bằng biểu đồ, bằng công thức hoặc mô tả bằng lời.
2. Đồ thị của hàm số
| Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng tọa độ đối với mọi x thuộc D. |
3. Sự đồng biến, nghịch biến của hàm số
|
Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a; b), nếu \(\forall {x_1},{x_2} \in (a;b)\), \({x_1} < {x_2}\)\( \Rightarrow f({x_1}) < f({x_2})\). Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a; b), nếu \(\forall {x_1},{x_2} \in (a;b)\), \({x_1} < {x_2}\)\( \Rightarrow f({x_1}) > f({x_2})\). |
Chú ý:
- Đồ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải.
- Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường “đi xuống” từ trái sang phải.
B. Bài tập
Bài 1 (ví dụ): Bảng dưới đây cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở Thủ đô Hà Nội:
Nếu gọi x là thời điểm, y là nồng độ bụi PM 2.5 thì x là biến số và y là hàm số của x. Đó là hàm số được cho bằng bảng.
Tập xác định của hàm số là D = {0; 4; 8; 12; 16}.
Tập giá trị của hàm số là {74,27; 64,58; 57,9; 69,07; 81,78}.
Bài 2: Viết hàm số mô tả sự phụ thuộc của quãng đường đi được vào thời gian của một vật chuyển động thẳng đều với vận tốc 2 m/s. Tìm tập xác định của hàm số đó. Tính quãng đường vật đi được sau 5 s, 10 s.
Giải:
Một vật chuyển động thẳng đều với vận tốc v = 2 m/s thì quãng đường đi được S phụ thuộc vào thời gian t (giây) theo công thức S = 2t, trong đó t là biến số, S là hàm số của t.
Tập xác định của hàm số là D = [0; +∞).
Quãng đường vật đi được sau 5 s: \({S_1} = S(5) = 2.5 = 10\) (m).
Quãng đường vật đi được sau 10 s: \({S_2} = S(10) = 2.10 = 20\) (m).
Bài 3: Tìm tập xác định của các hàm số sau:
a) \(y = \sqrt {2x - 4} \).
b) \(y = \frac{1}{{x - 1}}\).
Giải:
a) Biểu thức \(\sqrt {2x - 4} \) có nghĩa khi \(2x - 4 \ge 0\), tức là khi \(x \ge 2\).
Vậy tập xác định của hàm số đã cho là \(D = [2; + \infty )\).
b) Biểu thức \(\frac{1}{{x - 1}}\) có nghĩa khi \(x - 1 \ne 0\), tức là khi \(x \ne 1\).
Vậy tập xác định của hàm số đã cho là \(D = \mathbb{R}\backslash \{ 1\} \).
Bài 4:
a) Cho hàm số \(y = f(x) = \frac{1}{8}{x^2}\) xác định trên D = [-3;5] có đồ thị (C) như hình.
- Điểm A(4; f(4)) có thuộc đồ thị (C) không?
- Lấy điểm B tùy ý trên đồ thị (C). Nêu nhận xét về hoành độ của điểm B.
b) Vẽ đồ thị hàm số y = f(x) được cho bởi bảng sau:
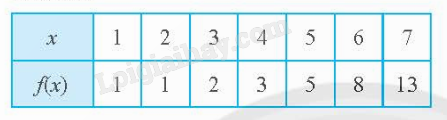
Giải:
a) Vì \(4 \in [ - 3;5]\) nên điểm A có hoành độ bằng 4 và tung độ \(y = \frac{1}{8}{.4^2} = 2\) là điểm thuộc đồ thị (C).
Khi lấy điểm B tùy ý trên đồ thị (C) thì hoành độ
\({x_B}\) của điểm này thuộc tập xác định D, nghĩa là \( - 3 \le {x_B} \le 5\).
b) Đồ thị hàm số gồm 7 điểm như hình:
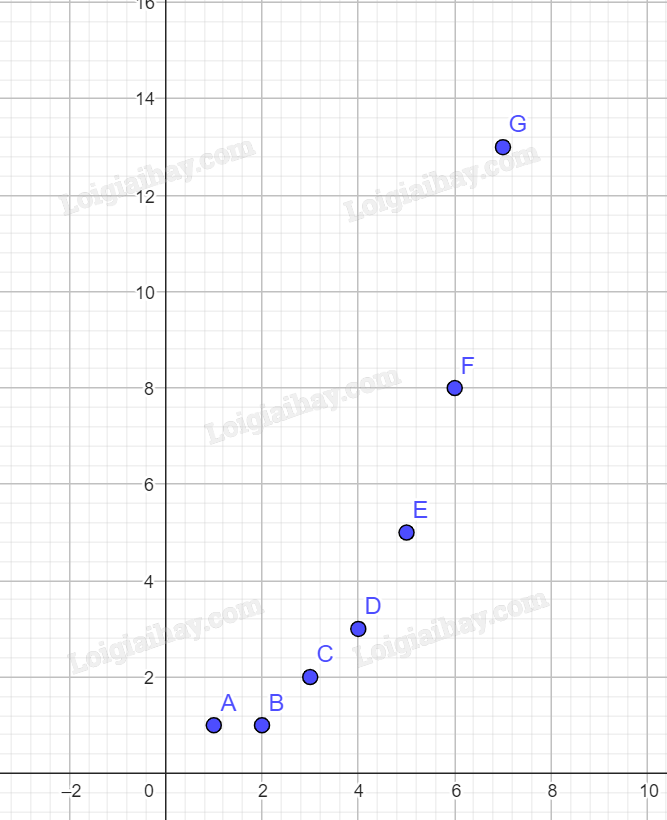
Bài 5: Hàm số \(y = {x^2}\) đồng biến hay nghịch biến trên mỗi khoảng \(( - \infty ;0)\) và \((0; + \infty )\)?
Giải:
Vẽ đồ thị hàm số \(y = f(x) = {x^2}\) như hình:
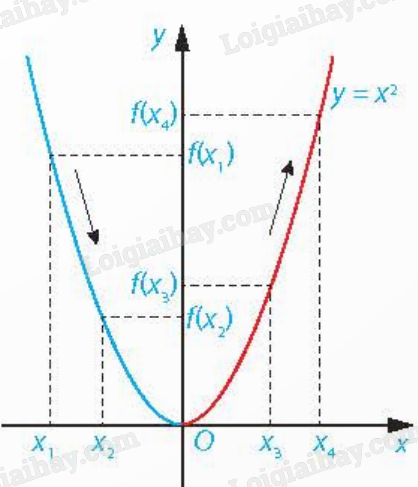
- Trên khoảng \(( - \infty ;0)\), đồ thị “đi xuống” từ trái sang phải và với \({x_1},{x_2} \in ( - \infty ;0)\), \({x_1} < {x_2}\) thì \(f({x_1}) > f({x_2})\).
Như vậy, hàm số \(y = {x^2}\) nghịch biến trên khoảng \(( - \infty ;0)\).
- Trên khoảng \((0; + \infty )\), đồ thị “đi lên” từ trái sang phải và với \({x_3},{x_4} \in (0; + \infty )\), \({x_3} < {x_4}\) thì \(f({x_3}) < f({x_4})\).
Như vậy, hàm số \(y = {x^2}\) đồng biến trên khoảng \((0; + \infty )\).
Bình luận
Chia sẻ
- Giải mục 1 trang 5, 6 SGK Toán 10 tập 2 - Kết nối tri thức
- Giải mục 2 trang 7 SGK Toán 10 tập 2 - Kết nối tri thức
- Giải mục 3 trang 8 SGK Toán 10 tập 2 - Kết nối tri thức
- Giải bài 6.1 trang 9 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.2 trang 9 SGK Toán 10 – Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức
