-
GIẢI SGK TOÁN 10 KẾT NỐI TRI THỨC VỚI CUỘC SỐNG - MỚI NHẤT
-
Toán 10 tập 1 - Kết nối tri thức với cuộc sống
-
Toán 10 tập 2 - Kết nối tri thức với cuộc sống
Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống
Bài 16. Hàm số bậc hai Toán 10 Kết nối tri thức
Lý thuyết Hàm số bậc hai - SGK Toán 10 Kết nối tri thức
A. Lý thuyết 1. Khái niệm hàm số bậc hai
A. Lý thuyết
1. Khái niệm hàm số bậc hai
|
Hàm số bậc hai là hàm số cho bởi công thức \(y = a{x^2} + bx + c\), trong đó x là biến số, a, b, c là các hằng số và \(a \ne 0\). Tập xác định của hàm số bậc hai là \(\mathbb{R}\). |
Nhận xét: Hàm số \(y = a{x^2}\) \((a \ne 0)\) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với b = c = 0.
2. Đồ thị của hàm số bậc hai
|
Hàm số bậc hai \(y = a{x^2} + bx + c\) \((a \ne 0)\) có đồ thị là một đường parabol có đỉnh là điểm \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\), có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}}\). Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0. Để vẽ đường parabol \(y = a{x^2} + bx + c\) ta tiến hành theo các bước sau: 1. Xác định tọa độ đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\). 2. Xác định trục đối xứng \(x = - \frac{b}{{2a}}\). 3. Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol. 4. Vẽ parabol. |
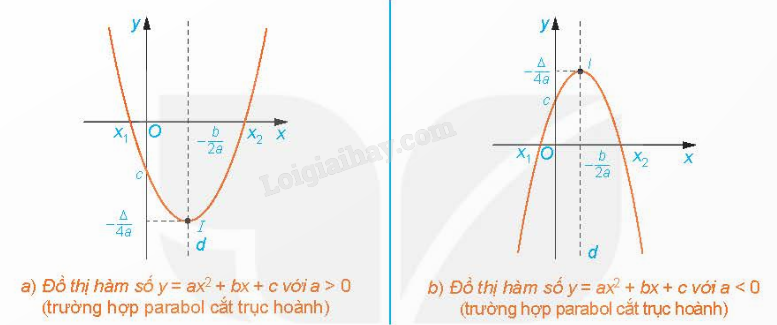
Nhận xét: Từ đồ thị hàm số \(y = a{x^2} + bx + c\) \((a \ne 0)\), ta suy ra tính chất của hàm số \(y = a{x^2} + bx + c\) \((a \ne 0)\):
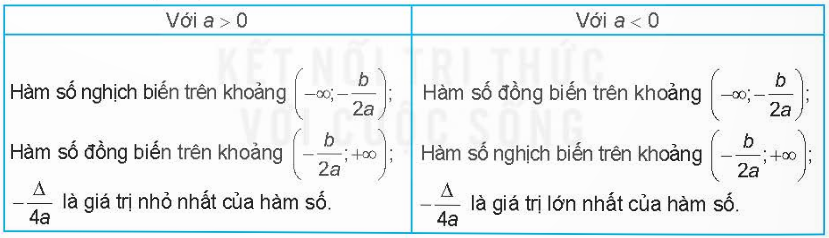
B. Bài tập
Bài 1: Hàm số nào dưới đây là hàm số bậc hai?
A. \(y = {x^2} + 3{x^2} + 2\)
B. \(y = \frac{1}{{{x^2}}}\)
C. \(y = - 3{x^2} + 1\)
D. \(y = 3{\left( {\frac{1}{x}} \right)^2} - 3\frac{1}{x} - 1\)
Giải:
Hàm số \(y = - 3{x^2} + 1\) là hàm số bậc hai với a = -3, b = 0, c = 1. Hàm số thỏa mãn điều kiện \(a \ne 0\) \(( - 3 \ne 0)\) và có tập xác định là \(\mathbb{R}\).
Bài 2:
a) Vẽ parabol \(y = - 2{x^2} - 2x + 4\).
b) Từ đồ thị, hãy tìm khoảng đồng biến, nghịch biến và giá trị lớn nhất của hàm số \(y = - 2{x^2} - 2x + 4\).
Giải:
a) Ta có a = -2 < 0 nên parabol quay bề lõm xuống dưới.
Đỉnh \(I\left( { - \frac{1}{2};\frac{9}{2}} \right)\). Trục đối xứng \(x = - \frac{1}{2}\). Giao điểm của đồ thị với trục Oy là A(0;4). Parabol cắt trục hoành tại điểm có hoành độ là nghiệm của phương trình \( - 2{x^2} - 2x + 4 = 0\), tức là x = 1 và x = -2.
Để vẽ đồ thị chính xác hơn, ta có thể lấy thêm điểm đối xứng vói A qua trục đối xứng \(x = - \frac{1}{2}\) là B(-1;4).
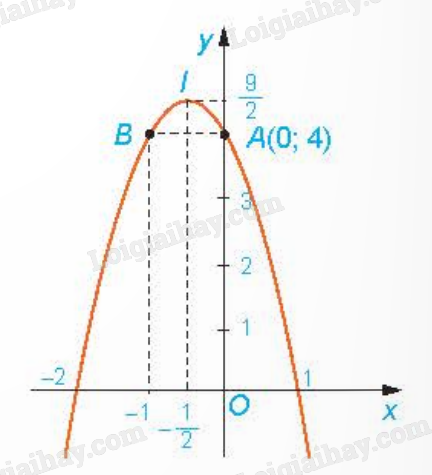
b) Từ đồ thị ta thấy:
Hàm số \(y = - 2{x^2} - 2x + 4\) đồng biến trên \(\left( { - \infty ; - \frac{1}{2}} \right)\), nghịch biến trên \(\left( { - \frac{1}{2}; + \infty } \right)\).
Giá trị lớn nhất của hàm số là \(y = \frac{9}{2}\) khi \(x = - \frac{1}{2}\).
Bình luận
Chia sẻ
- Giải mục 1 trang 11, 12 SGK Toán 10 tập 2 - Kết nối tri thức
- Giải mục 2 trang 12, 13, 14, 15 SGK Toán 10 tập 2 - Kết nối tri thức
- Giải bài 6.7 trang 16 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.8 trang 16 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.9 trang 16 SGK Toán 10 – Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
Các bài khác cùng chuyên mục
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức
