Bài 3. Hai đường thẳng song song trang 76 SGK Toán 7 ch..

Giải mục 3 trang 79, 80 SGK Toán 7 tập 1 - Chân trời sáng tạo

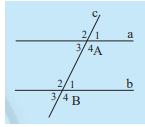
Em hãy: - Vẽ hai đường thẳng a và b song song với nhau. - Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B. a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này. b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.

Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên...

Video hướng dẫn giải

Lựa chọn câu để xem lời giải nhanh hơn

HĐ 3

Em hãy:

- Vẽ hai đường thẳng a và b song song với nhau.

- Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B.

a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này.

b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.

Phương pháp giải:

Vẽ hình.

Đo và nhận xét

Lời giải chi tiết:

a) Một cặp góc so le trong là góc A₃ và góc B₁ . Hai góc này cùng có số đo là 60 \(^\circ \) nên chúng bằng nhau .

b) Một cặp góc đồng vị là góc A₁ và góc B₁ . Hai góc này cùng có số đo là 60 \(^\circ \) nên chúng bằng nhau .

Thực hành 4

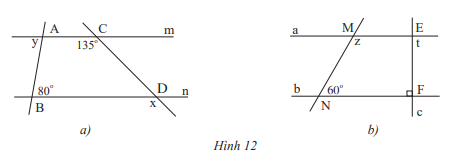
Cho biết m // n và a // b. Tính số đo x,y,z và t của các góc trong hình 12.

Phương pháp giải:

Sử dụng tính chất của 2 đường thẳng song song:

Một đường thẳng cắt hai đường thẳng song song thì:

+ 2 góc so le trong bằng nhau

+ 2 góc đồng vị bằng nhau

Lời giải chi tiết:

a) Vì m // n nên x = 135\(^\circ \)( 2 góc đồng vị) ; y = 80\(^\circ \) ( 2 góc so le trong)

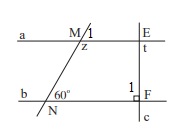
Vì a // b nên \(\widehat {{M_1}} = 60^\circ \) ( 2 góc đồng vị)

Mà \(\widehat {{M_1}} + z = 180^\circ \) ( 2 góc kề bù) nên z = 180\(^\circ \)- 60\(^\circ \)=120\(^\circ \)

Vì a // b nên \(\widehat {{F_1}} = t\) ( 2 góc so le trong), mà \(\widehat {{F_1}} = 90^\circ \) nên t = 90\(^\circ \)

Vận dụng 1

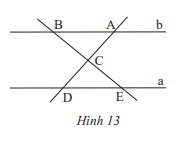
Tìm các cặp góc bằng nhau của hai tam giác ABC và DEC trong Hình 13, biết a // b.

Phương pháp giải:

*2 góc đối đỉnh thì bằng nhau

*Sử dụng tính chất của 2 đường thẳng song song: Một đường thẳng cắt hai đường thẳng song song thì:

+ 2 góc so le trong bằng nhau

+ 2 góc đồng vị bằng nhau.

Lời giải chi tiết:

Vì a // b nên \(\widehat {BAC} = \widehat {CDE};\widehat {ABC} = \widehat {CED}\) (2 góc so le trong)

Ta có: \(\widehat {ACB} = \widehat {DCE}\) ( 2 góc đối đỉnh).

Vận dụng 2

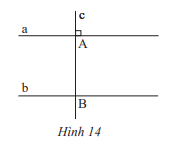
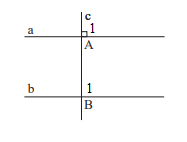
Cho hai đường thẳng a, b song song với nhau, đường thẳng c vuông góc với a tại A và cắt b tại B. Hãy giải thích tại sao đường thẳng c cũng vuông góc với b.

Phương pháp giải:

Sử dụng tính chất của 2 đường thẳng song song: Một đường thẳng cắt hai đường thẳng song song thì 2 góc đồng vị bằng nhau.

Lời giải chi tiết:

Vì a // b nên \(\widehat {{B_1}} = \widehat {{A_1}}\) (2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \) nên \(\widehat {{B_1}} = 90^\circ \).

Vậy c vuông góc với b.

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 7 phiếu

Bài tiếp theo

Giải bài 1 trang 80 SGK Toán 7 tập 1 - Chân trời sáng tạo
Trong Hình 15, cho biết a // b, Tìm số đo các góc đỉnh A và B
Giải bài 2 trang 80 SGK Toán 7 tập 1 - Chân trời sáng tạo
Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó. a) Vì sao cặp góc so le trong còn lại cũng bằng nhau? b) Vì sao các cặp góc đồng vị cũng bằng nhau?
Giải bài 3 trang 80 SGK Toán 7 tập 1 - Chân trời sáng tạo
Hãy nói các cách để kiểm tra hai đường thẳng song song mà em biết
Giải bài 4 trang 80 SGK Toán 7 tập 1 - Chân trời sáng tạo
Cho Hình 16, biết a // b. a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc
Giải bài 5 trang 80 SGK Toán 7 tập 1 - Chân trời sáng tạo
Cho Hình 17, biết a // b. Tính số đo các góc
Giải bài 6 trang 81 SGK Toán 7 tập 1 - Chân trời sáng tạo
Cho Hình 18, biết (widehat {{B_1}} = 40^circ ,widehat {{C_2}} = 40^circ ) a) Đường thẳng a có song song với đường thẳng b không? Vì sao? b) Đường thẳng b có song song với đường thẳng c không? Vì sao? c) Đường thẳng a có song song với đường thẳng c không? Vì sao?
Giải bài 7 trang 81 SGK Toán 7 tập 1 - Chân trời sáng tạo
Quan sát Hình 19 và cho biết: a) Vì sao m // n?
Giải mục 2 trang 78, 79 SGK Toán 7 tập 1 - Chân trời sáng tạo
Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8...a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua A và song song với BC, vẽ đường thẳng b đi qua B và song song với AC. b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?
Giải mục 1 trang 76, 77 SGK Toán 7 tập 1 - Chân trời sáng tạo
Quan sát Hình 3 và dự đoán các đường thẳng nào song song với nhau...Tìm các cặp đường thẳng song song trong Hình 5 và giải thích.
Giải câu hỏi mở đầu trang 76 SGK Toán 7 tập 1 - Chân trời sáng tạo
Có dấu hiệu gì về số đo của các góc đỉnh A và các góc đỉnh B trong hình bên để nhận biết hai đường thằng song song hay không?
Lý thuyết Hai đường thẳng song song SGK Toán 7 Chân trời sáng tạo
1. Dấu hiệu nhận biết hai đường thẳng song song