Bài 4. Ba đường conic trong mặt phẳng tọa độ Toán 10 Ch..

Giải mục 3 trang 68, 69, 70 SGK Toán 10 tập 2 - Chân trời sáng tạo

Viết phương trình chính tắc của parabol (P) có đường chuẩn Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m

Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Lựa chọn câu để xem lời giải nhanh hơn

HĐ Khám phá 5

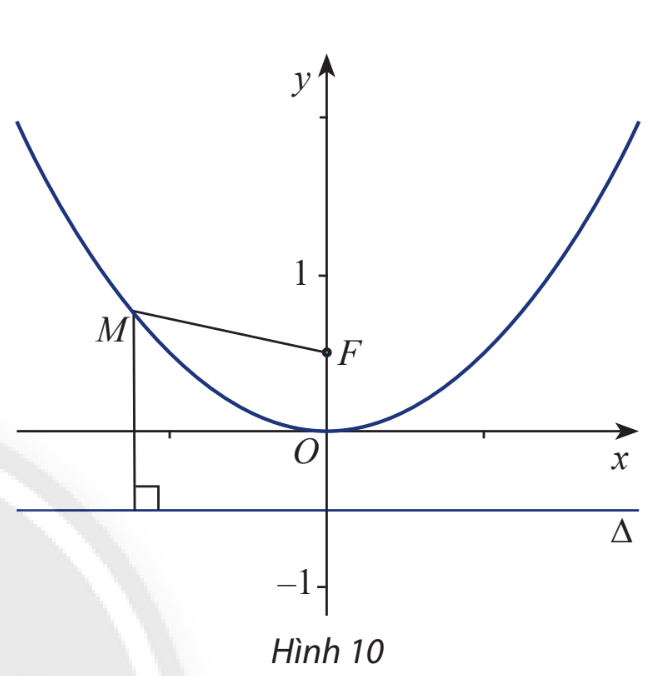
Trong mặt phẳng Oxy, cho điểm $F\left( {0;\frac{1}{2}} \right)$ , đường thẳng $\Delta :y + \frac{1}{2} = 0$ và điểm $M(x;y)$ . Để tìm hệ thức giữa x và y sao cho $M$ cách đều F và $\Delta$ , một học sinh đã làm như sau:

+) Tính MF và MH (với H là hình chiếu của M trên $\Delta$ ):

$MF = \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} ,MH = d\left( {M,\Delta } \right) = \left| {y + \frac{1}{2}} \right|$

+) Điều kiện để M cách đều F và $\Delta$ :

$\begin{array}{l}MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} = \left| {y + \frac{1}{2}} \right|\\ \Leftrightarrow {x^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {y + \frac{1}{2}} \right)^2}\\ \Leftrightarrow {x^2} = 2y \Leftrightarrow y = \frac{1}{2}{x^2}\left( * \right)\end{array}$

Hãy cho biết tên đồ thị (P) của hàm số (*) vừa tìm được.

Lời giải chi tiết:

Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.

HĐ Khám phá 6

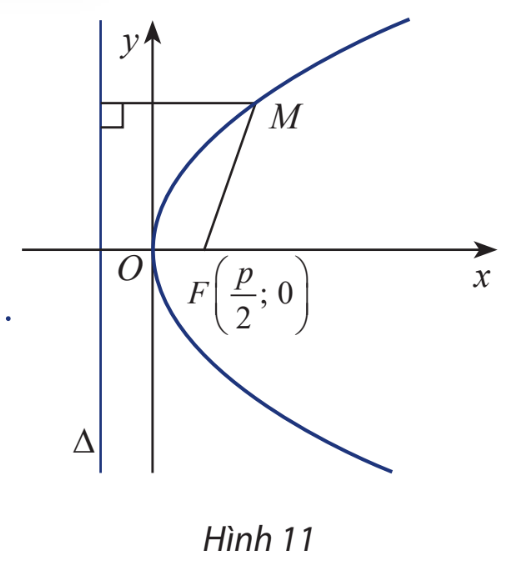
Cho parabol (P) có tiêu điểm F và đường chuẩn $\Delta$ . Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên $p > 0$ .

Chọn hệ trục tọa độ Oxy sao cho $F\left( {\frac{p}{2};0} \right)$ và $\Delta :x + \frac{p}{2} = 0$ .

Xét điểm $M(x;y)$ .

a) Tính MF và $d\left( {M,\Delta } \right)$ .

b) Giải thích biểu thức sau:

$M(x;y) \in (P) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|$ .

Phương pháp giải:

Sử dụng phương pháp tọa độ trong mặt phẳng.

Lời giải chi tiết:

a) Ta có: $\overrightarrow {FM} = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}}$ .

$d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|$ .

b) M thuộc parabol (P) nên M cách đều F và $\Delta$ .

Suy ra $MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x - \frac{p}{2}} \right|$ .

Thực hành 3

Viết phương trình chính tắc của parabol (P) có đường chuẩn $\Delta :x + 1 = 0$ .

Phương pháp giải:

Bước 1: Từ phương trình đường chuẩn tìm tọa độ của tiêu điểm (phương trình đường chuẩn có dạng $x + \frac{p}{2} = 0$ .

Bước 2: Viết phương trình chính tắc của parabol có dạng ${y^2} = 2px$ với $M(x;y) \in (P)$ .

Lời giải chi tiết:

Từ phương trình đường chuẩn $\Delta :x + 1 = 0$ ta có tiêu điểm $F\left( {1;0} \right)$ .

Phương trình chính tắc của parabol có dạng ${y^2} = 2x$ .

Vận dụng 3

Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.

Phương pháp giải:

Bước 1: Gọi phương trình của parabol một cách tổng quát.

Bước 2: Thay các giả thiết tìm tiêu điểm.

Bước 3: Thay $x = 2$ vào phương trình chính tắc tìm y.

Lời giải chi tiết:

Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới.

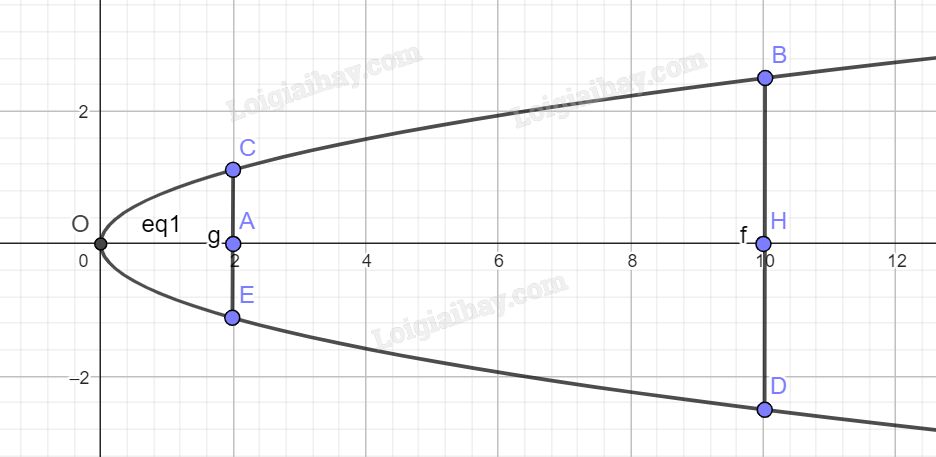
Gọi phương trình của parabol là ${y^2} = 2px$ .

Ta có chiều cao của cổng $OH = 10$ , chiều rộng tại chân cổng $BD = 2BH = 5$ .

Vậy điểm B có tọa độ là $B\left( {10;\frac{5}{2}} \right)$ .

Thay tọa độ điểm B vào phương trình parabol ta có:

${\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}$ , suy ra phương trình parabol có dạng ${y^2} = \frac{5}{8}x$ .

Thay $x = 2$ vào phương trình ${y^2} = \frac{5}{8}x$ ta tìm được $y = CA = \frac{{\sqrt 5 }}{2}$ .

Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là $\sqrt 5$ m.

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 11 phiếu

Bài tiếp theo

Giải bài 1 trang 70 SGK Toán 10 tập 2 – Chân trời sáng tạo
Viết phương trình chính tắc của: a) Elip có trục lớn bằng 20 và trục nhỏ bằng 16
Giải bài 2 trang 70 SGK Toán 10 tập 2 – Chân trời sáng tạo
Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ của các tiêu điểm của chúng
Giải bài 3 trang 70 SGK Toán 10 tập 2 – Chân trời sáng tạo
Để cắt một bảng hiệu quảng cáo hình Elip có trục lớn là 80 cm và trục nhỏ là 40 cm từ một tấm ván ép hình chữ nhật có kích thước là 80 cm x 40 cm, người ta vẽ hình elip đó trên tấm ván ép như hướng dẫn sau:
Giải bài 4 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8 m, rộng 20 m (hình 16) a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên b) Tính khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm
Giải bài 5 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một tháp làm nguội của một nhà máy có mặt cắt là hình hyperbol có phương trình
Giải bài 6 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một cái cầu có dây cáp treo như hình vẽ parabol, cầu dài 100 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m (hình 18). Tính chiều dài của thanh cách điểm giữa cầu 18m
Giải Thử thách trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo
Áp dụng tính chất quang học của parabol để giải quyết vẫn đề sau đây:
Giải mục 2 trang 65, 66, 67 SGK Toán 10 tập 2 - Chân trời sáng tạo
Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6. Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình
Giải mục 1 trang 64, 65 SGK Toán 10 tập 2 - Chân trời sáng tạo
Viết phương trình chính tắc của elip trong hình 4 Một đường hầm có mặt các hình nửa Elip cao 4 m, rộng 10 m (hình 5). Viết phương trình chính tắc của elip đó.
Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
A. Lý thuyết 1. Elip a) Nhận biết elip

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.