Giải bài 4 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo

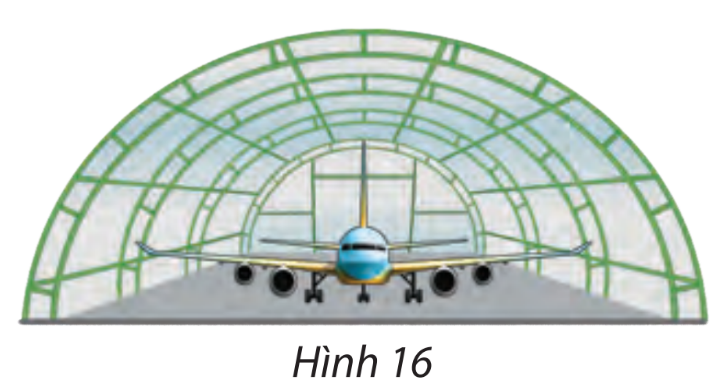
Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8 m, rộng 20 m (hình 16) a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên b) Tính khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm

Đề bài

Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8 m, rộng 20 m (hình 16)

a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên

b) Tính khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm

Phương pháp giải - Xem chi tiết

a) Bước 1: Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm

Bước 2: Viết phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (E);b = \sqrt {{a^2} - {c^2}} \)

b) Bước 1: Từ dữ kiện cách chân tường 5 m, xác định cách gốc tạo độ bao nhiêu (x=?)

Bước 2: Thay x vừa tìm được vào phương trình chính tắc tìm y

Lời giải chi tiết

a) Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm, trục tung thẳng đứng

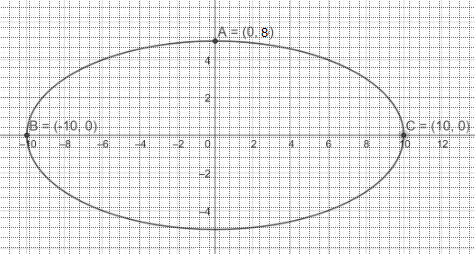
Nhà vòm có dạng elip nên có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (với a,b>0)

Ta có chiều cao 8 m nên \(OA = b = 8\), chiều rộng của vòm là 20 m, suy ra \(BC = 2a = 20 \Rightarrow a = 10\).

Suy ra, phương trình miêu tả hình dáng nhà vòm là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)

b) Điểm đó cách chân tưởng 5 m tương ứng cách tâm 5 m (vì từ tâm vòm đến tưởng là 10 m)

Thay \(x = 5\) vào phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\), ta tìm được \(y = 4\sqrt 3 \)

Vậy khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm là \(4\sqrt 3\) m

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 14 phiếu

Bài tiếp theo

Giải bài 5 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một tháp làm nguội của một nhà máy có mặt cắt là hình hyperbol có phương trình
Giải bài 6 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một cái cầu có dây cáp treo như hình vẽ parabol, cầu dài 100 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m (hình 18). Tính chiều dài của thanh cách điểm giữa cầu 18m
Giải Thử thách trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo
Áp dụng tính chất quang học của parabol để giải quyết vẫn đề sau đây:
Giải bài 3 trang 70 SGK Toán 10 tập 2 – Chân trời sáng tạo
Để cắt một bảng hiệu quảng cáo hình Elip có trục lớn là 80 cm và trục nhỏ là 40 cm từ một tấm ván ép hình chữ nhật có kích thước là 80 cm x 40 cm, người ta vẽ hình elip đó trên tấm ván ép như hướng dẫn sau:
Giải bài 2 trang 70 SGK Toán 10 tập 2 – Chân trời sáng tạo
Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ của các tiêu điểm của chúng
Giải bài 1 trang 70 SGK Toán 10 tập 2 – Chân trời sáng tạo
Viết phương trình chính tắc của: a) Elip có trục lớn bằng 20 và trục nhỏ bằng 16
Giải mục 3 trang 68, 69, 70 SGK Toán 10 tập 2 - Chân trời sáng tạo
Viết phương trình chính tắc của parabol (P) có đường chuẩn Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m
Giải mục 2 trang 65, 66, 67 SGK Toán 10 tập 2 - Chân trời sáng tạo
Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6. Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình
Giải mục 1 trang 64, 65 SGK Toán 10 tập 2 - Chân trời sáng tạo
Viết phương trình chính tắc của elip trong hình 4 Một đường hầm có mặt các hình nửa Elip cao 4 m, rộng 10 m (hình 5). Viết phương trình chính tắc của elip đó.