Giải mục 3 trang 41, 42, 43, 44 SGK Toán 10 tập 2 - Chân trời sáng tạo
Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh a) Tìm tọa độ trung điểm M của cạnh QS b) Tìm tọa độ trọng tâm G của tam giác QRS
HĐ Khám phá 5
Cho hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm tọa độ vectơ \(\overrightarrow {AB} \) theo tọa độ hai điểm A,B
Phương pháp giải:
Với \(\overrightarrow v = \left( {{v_1};{v_2}} \right),\overrightarrow w = \left( {{w_1};{w_2}} \right)\) thì \(\overrightarrow v + \overrightarrow w \) là \(\left( {{v_1} + {w_1};{v_2} + {w_2}} \right)\)
Lời giải chi tiết:
Ta có tọa độ vectơ \(\overrightarrow {OB} ,\overrightarrow {OA} \) chính là tọa độ điểm B và A
Nên ta có \(\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OA} = \left( {{x_A};{y_A}} \right)\)
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {{x_B};{y_B}} \right) - \left( {{x_A};{y_A}} \right) = ({x_B} - {x_A};{y_B} - {y_A})\)
Thực hành 3
Cho \(E\left( {9;9} \right),F\left( {8; - 7} \right),G\left( {0; - 6} \right)\). Tìm tọa độ các vectơ \(\overrightarrow {FE} ,\overrightarrow {FG} ,\overrightarrow {EG} \)
Phương pháp giải:
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\)
Lời giải chi tiết:
Ta có
\(\begin{array}{l}\overrightarrow {FE} = ({x_E} - {x_F};{y_E} - {y_F}) = (9 - 8;9 - ( - 7)) = (1;16)\\\overrightarrow {FG} = ({x_G} - {x_F};{y_G} - {y_F}) = (0 - 8;( - 6) - ( - 7)) = ( - 8;1)\\\overrightarrow {EG} = ({x_G} - {x_E};{y_G} - {y_E}) = (0 - 9;( - 6) - 9) = ( - 9; - 15)\end{array}\)
HĐ Khám phá 6
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh là \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\). Gọi \(M\left( {{x_M};{y_M}} \right)\) là trung điểm của đoạn thẳng AB, \(G\left( {{x_G};{y_G}} \right)\) là trọng tâm của tam giác ABC
a) Biểu thị vectơ \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \)
b) Biểu thị vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \), \(\overrightarrow {OB} \) và \(\overrightarrow {OC} \)
c) Từ các kết quả trên, tìm tọa độ điểm M, G theo tọa độ của các điểm A, B, C
Phương pháp giải:
a) Sử dụng tính chất trung điểm \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\) (với M là trung điểm của đoạn thẳng AB)
b) Sử dụng tính chất trọng tâm \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\) (với G là trọng tâm của tam giác ABC)
c) Thay tọa độ các điểm vào và xác định
Lời giải chi tiết:
a) M là trung điểm của đoạn thẳng AB, áp dụng tính chất trung điểm ta có:
\(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) G là trọng tâm của tam giác ABC, áp dụng tính chất trọng tâm của tam giác ta có:
\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
c) Ta có \(\overrightarrow {OA} = \left( {{x_A};{y_A}} \right),\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OC} = \left( {{x_C};{y_C}} \right)\)
Suy ra:
\(\begin{array}{l}\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right)} \right]\\ = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\end{array}\)
\(\begin{array}{l}
\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right) + \left( {{x_c};{y_c}} \right)} \right]\\
= \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)
\end{array}\)
Mà ta có tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ điểm M, nên ta có
Tọa độ điểm M là \(\left( {{x_M};{y_M}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm G là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Thực hành 4
Cho tam giác QRS có tọa độ các đỉnh \(Q\left( {7; - 2} \right),R( - 4;9)\) và \(S(5;8)\).
a) Tìm tọa độ trung điểm M của cạnh QS.
b) Tìm tọa độ trọng tâm G của tam giác QRS.
Phương pháp giải:
Tọa độ điểm M là \(\left( {\frac{{{x_Q} + {x_S}}}{2};\frac{{{y_Q} + {y_S}}}{2}} \right)\).
Tọa độ điểm G là \(\left( {\frac{{{x_Q} + {x_R} + {x_S}}}{3};\frac{{{y_Q} + {y_R} + {y_S}}}{3}} \right)\).
Lời giải chi tiết:
a) \({x_M} = \frac{{{x_Q} + {x_S}}}{2} = \frac{{7 + 5}}{2} = 6; \\{y_M} = \frac{{{y_Q} + {y_S}}}{2} = \frac{{( - 2) + 8}}{2} = 3\).
Vậy \(M\left( {6;3} \right)\).
b)
\({x_G} = \frac{{{x_Q} + {x_S} + {x_R}}}{3} = \frac{{7 + ( - 4) + 5}}{3} = \frac{8}{3};\\{y_M} = \frac{{{y_Q} + {y_S} + {y_R}}}{3} = \frac{{( - 2) + 9 + 8}}{3} = 5\).
Vậy \(G\left( {\frac{8}{3};5} \right)\).
HĐ Khám phá 7
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2}),\overrightarrow b = ({b_1};{b_2})\) và hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Hoàn thành các phép biến đổi sau:
a) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = ...?\)
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = t{b_1}\\{a_2} = t{b_2}\end{array} \right.\) hay \(\left\{ \begin{array}{l}{b_1} = k{a_1}\\{b_2} = k{a_2}\end{array} \right. \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = ...?\)
c) \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( {\overrightarrow a } \right)}^2}} = \sqrt {.?.} \)
d) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A}) \Rightarrow AB = \sqrt {{{\left( {\overrightarrow {AB} } \right)}^2}} = \sqrt {.?.} \)
e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{.?.}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\) (\(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \))
Lời giải chi tiết:
a) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = 0\)
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = t{b_1}\\{a_2} = t{b_2}\end{array} \right.\) hay \(\left\{ \begin{array}{l}{b_1} = k{a_1}\\{b_2} = k{a_2}\end{array} \right.\)
\( \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = {a_1}.k{a_2} - {a_2}.k{a_1} = 0\)
c) \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( {\overrightarrow a } \right)}^2}} = \sqrt {{a_1}^2 + {a_2}^2} \)
d) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A}) \Rightarrow AB = \sqrt {{{\left( {\overrightarrow {AB} } \right)}^2}} \)
\( = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \)
e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{a_1}{b_1} + {a_2}{b_2}}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\)
Thực hành 5
Trong mặt phẳng Oxy, cho tam giác DEF có tọa độ các đỉnh \(D(2;2),E(6;2)\) và \(F(2;6)\)
a) Tìm tọa độ điểm H là chân đường vuông cao của tam giác DEF kẻ từ D
b) Giải tam giác DEF
Phương pháp giải:
Bước 1: Tìm tọa độ các vectơ \(\overrightarrow {DH} ,\overrightarrow {EF} \)
Bước 2: Dựa vào ứng dụng tọa độ của các phép toán vectơ (tính chất vuông góc)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {EF} = \left( { - 2;4} \right)\)
Gọi tọa độ điểm H là \(\left( {x;y} \right)\) ta có \(\overrightarrow {DH} = \left( {x - 2;y - 2} \right),\overrightarrow {EH} = \left( {x - 6;y - 2} \right)\)
H là chân đường cao nên \(\overrightarrow {DH} \bot \overrightarrow {EF} \)
\(\begin{array}{l}\overrightarrow {DH} \bot \overrightarrow {EF} \Leftrightarrow \left( {x - 2} \right).\left( { - 2} \right) + \left( {y - 2} \right).4 = 0\\ \Leftrightarrow - 2x + 4y - 4 = 0\end{array}\) (1)
Hai vectơ \(\overrightarrow {EH} ,\overrightarrow {EF} \) cùng phương
\( \Leftrightarrow \left( {x - 6} \right).( - 2) - \left( {y - 2} \right).4 = 0 \Leftrightarrow - 2x - 4y + 20 = 0\) (2)
Từ (1) và (2) ta có hệ phương trình
\(\left\{ \begin{array}{l} - 2x + 4y - 4 = 0\\ - 2x - 4y + 20 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\)
Vậy \(H(4;3)\)
b) Ta có: \(\overrightarrow {DE} = (4;0),\overrightarrow {DF} = (0;4),\overrightarrow {EF} = ( - 4;4)\)
Suy ra: \(DE = \left| {\overrightarrow {DE} } \right| = \sqrt {{4^2} + {0^2}} = 4,DF = \left| {\overrightarrow {DF} } \right| = \sqrt {{0^2} + {4^2}} = 4\)
\(EF = \left| {\overrightarrow {EF} } \right| = \sqrt {{{( - 4)}^2} + {4^2}} = 4\sqrt 2 \)
\(\begin{array}{l}\cos D = \cos \left( {\overrightarrow {DE} ,\overrightarrow {DF} } \right) = \frac{{\overrightarrow {DE} .\overrightarrow {DF} }}{{DE.DF}} = \frac{{4.0 + 0.4}}{{4.4}} = 0 \Rightarrow \widehat D = 90^\circ \\\cos E = \cos \left( {\overrightarrow {ED} ,\overrightarrow {EF} } \right) = \frac{{\overrightarrow {ED} .\overrightarrow {EF} }}{{ED.EF}} = \frac{{\left( { - 4} \right).\left( { - 4} \right) + 0.4}}{{4.4\sqrt 2 }} = \frac{{\sqrt 2 }}{2} \Rightarrow \widehat E = 45^\circ \\\widehat F = 180^\circ - \widehat D - \widehat E = 180^\circ - 90^\circ - 45^\circ = 45^\circ \end{array}\)
Vận dụng 3
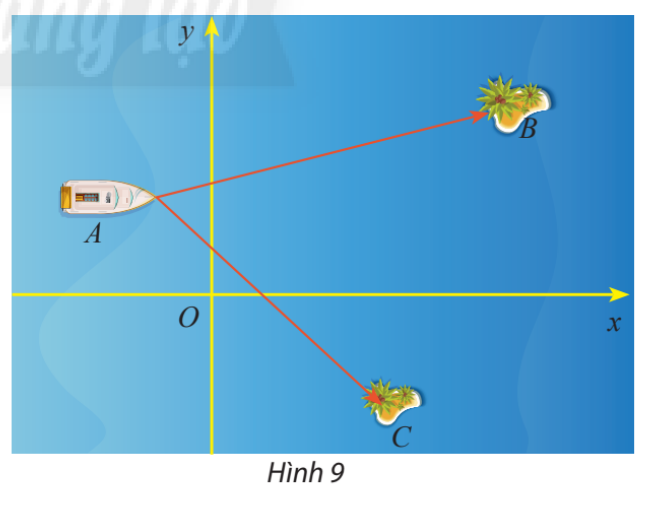
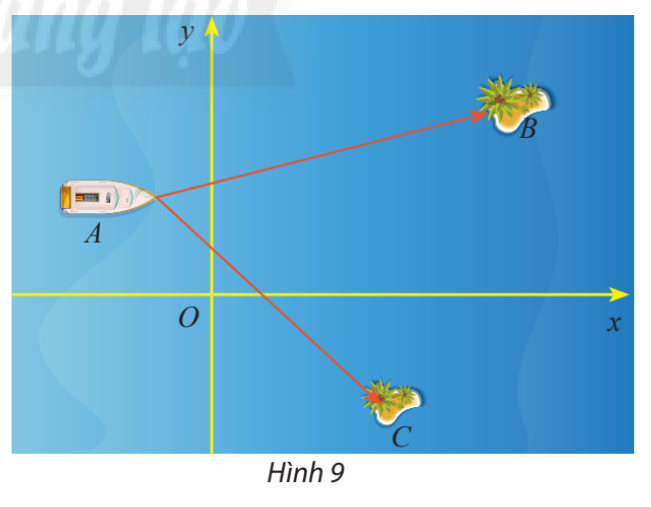
Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ \(B\left( {50;30} \right)\) và \(C\left( {32; - 23} \right)\). Một con tàu đang neo đậu tại điểm \(A\left( { - 10;20} \right)\)
a) Tính số đo của \(\widehat {BAC}\)
b) Cho biết một đơn vị trên hệ trục tọa độ tương ứng với 1km. Tính khoảng cách từ con tàu đến mỗi hòn đảo
Phương pháp giải:
Bước 1: Xác định tọa độ các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \)
Bước 2:
a) \(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} \)
b) \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {(x_B - x_A)^2+(y_B-y_A)^2}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AB} = \left( {60;10} \right),\overrightarrow {AC} = \left( {42; - 43} \right),\overrightarrow {BC} = \left( { - 18; - 53} \right)\)
\(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{60.42 + 10.( - 43)}}{{\sqrt {{{60}^2} + {{10}^2}} .\sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} }} \simeq 0,572 \Rightarrow \widehat {BAC} \approx 55^\circ 8'\)
b)
Khoảng cách từ tàu đến đảo B là \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{60}^2} + {{10}^2}} = 10\sqrt {37} \) (km)
Khoảng cách từ tàu đến đảo B là \(AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} = \sqrt {3613} \) (km)
- Giải bài 1 trang 44 SGK Toán 10 tập 2 – Chân trời sáng tạo
- Giải bài 2 trang 45 SGK Toán 10 tập 2 – Chân trời sáng tạo
- Giải bài 3 trang 45 SGK Toán 10 tập 2 – Chân trời sáng tạo
- Giải bài 4 trang 45 SGK Toán 10 tập 2 – Chân trời sáng tạo
- Giải bài 5 trang 45 SGK Toán 10 tập 2 – Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo













Danh sách bình luận