Giải mục 2 trang 22, 23 SGK Toán 10 tập 1 - Kết nối tri thức

HĐ3

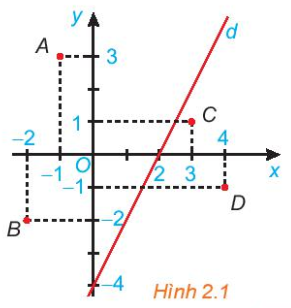
Cho đường thẳng d: 2x - y = 4 trên mặt phẳng toạ độ Oxy (H.2.1). Đường thẳng này chia mặt phẳng thành hai nửa mặt phẳng.

a) Các điểm 0,0; 0), A(-1; 3) và B(-2; -2) có thuộc cùng một nửa mặt phẳng bờ là đường thẳng d không?

Tính giá trị của biểu thức 2x - y tại các điểm đó và so sánh với 4.

b) Trả lời câu hỏi tương tự như câu a với các điểm C(3; 1), D(4; -1).

Phương pháp giải:

a)

Bước 1: Quan sát hình vẽ, nếu O, A, B nằm cùng một phía so với đường thẳng d thì 3 điểm đó cùng thuộc một nửa mặt phẳng bờ là đường thẳng d.

Bước 2: Thay tọa độ các điểm O, A, B vào biểu thức 2x-y và so sánh các giá trị tìm được với 4.

b)

Bước 1: Quan sát hình vẽ, nếu C, D nằm cùng một phía so với đường thẳng d thì 2 điểm đó cùng thuộc một nửa mặt phẳng bờ là đường thẳng d.

Bước 2: Thay tọa độ các điểm C, D vào biểu thức 2x-y và so sánh các giá trị tìm được với 4.

Lời giải chi tiết:

a)

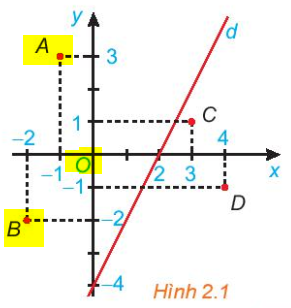
Bước 1:

Quan sát hình trên, các điểm A, O, B là các điểm được bôi vàng, và các điểm đó cùng nằm một phía (bên trái) nên chúng thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.

Bước 2:

+) Thay tọa độ của điểm O(0;0) vào biểu thức 2x-y ta được: 2.0-0=0.

Như vậy giá trị của biểu thức 2x-y tại O là 0 và 0<4.

+) Thay tọa độ của điểm A(-1;3) vào biểu thức 2x-y ta được: 2.(-1)-3=-5.

Như vậy giá trị của biểu thức 2x-y tại A là -5 và -5<4

+) Thay tọa độ của điểm B(-2;-2) vào biểu thức 2x-y ta được: 2.(-2)-(-2)=-2.

Như vậy giá trị của biểu thức 2x-y tại B là -2 và -2<4.

b) 

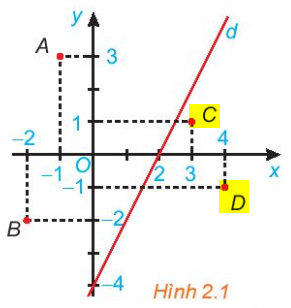
Bước 1:

Quan sát hình trên, các điểm C, D là các điểm được bôi vàng, và các điểm đó cùng nằm một phía (bên phải) nên chúng thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.

Bước 2:

+) Thay tọa độ của điểm C(3;1) vào biểu thức 2x-y ta được: 2.3-1=5.

Như vậy giá trị của biểu thức 2x-y tại C là 5 và 5>4.

+) Thay tọa độ của điểm D(4;-1) vào biểu thức 2x-y ta được: 2.4-(-1)=9.

Như vậy giá trị của biểu thức 2x-y tại D là 9 và 9>4

Chú ý

Khi thay tọa độ các điểm vào biểu thức 2x-y, nếu y là một giá trị âm thì cần đưa nguyên dấu vào trong biểu thức.

Luyện tập 2

Biểu diễn miền nghiệm của bất phương trình 2x+y<200

Phương pháp giải:

Ta biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax+b

Bước 1: Vẽ đường thẳng (nét đứt).

Bước 2: Lấy một điểm bất kì không thuộc d trên mặt phẳng rồi thay vào biểu thức ax+b. Xác định c có bằng 0 hay không, nếu c khác 0 thì ta lấy điểm để thay vào là gốc O(0;0).

Nếu O thỏa mãn bất phương trình thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng bờ d chứa điểm đã lấy.

Lời giải chi tiết:

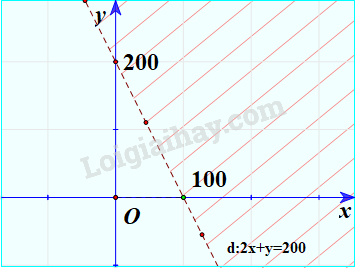
Ta biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn 2x+y<200

Bước 1: Vẽ đường thẳng d: 2x+y=200 trên mặt phẳng tọa độ Oxy.

Bước 2: Lấy một điểm bất kì không thuộc d trên mặt phẳng rồi thay vào biểu thức 2x+y. Chẳng hạn, lấy O(0;0), ta có: 2.0+0<200

Do đó miền nghiệm của bất phương trình đã cho là nửa mặt phẳng bờ d chứa gốc tọa độ không kể đường thẳng d. (miền không bị gạch).

Chú ý

Miền nghiệm của bất phương trình 2x+y

Vận dụng

Một công ty viễn thông tính phí 1 nghìn đồng mỗi phút gọi nội mạng và 2 nghìn đồng mỗi phút gọi ngoại mạng. Em có thể sử dụng bao nhiêu phút gọi nội mạng và bao nhiêu phút gọi ngoại mạng trong một tháng nếu em muốn số tiền phải trả ít hơn 200 nghìn đồng?

Phương pháp giải:

Bước 1: Gọi x là số phút gọi nội mạng (\(x \in \mathbb{N}\)), y là số phút gọi ngoại mạng (\(y \in \mathbb{N}\)) và biến đổi bài toán đã cho thành bài toán tìm miền nghiệm của bất phương trình.

Bước 2: Xác định miền nghiệm.

Lời giải chi tiết:

Bước 1:

Gọi x là số phút gọi nội mạng (\(x \ge 0\)), y là số phút gọi ngoại mạng (\(y \ge 0\)).

Số tiền cần phải trả là \(x + 2y\) nghìn đồng.

Để số tiền phải trả ít hơn 200 nghìn đồng thì \(x + 2y < 200\).

Như vậy, bài toán trở thành tìm miền nghiệm của bất phương trình \(x + 2y < 200\).

Bước 2:

Xác định miền nghiệm:

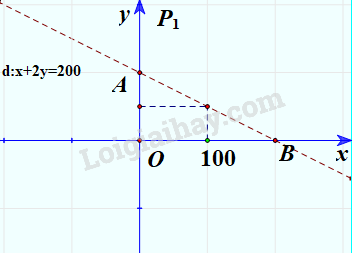
+ Vẽ đường thẳng d: x + 2y = 200 (nét đứt).

+ Thay tọa độ O(0;0) vào biểu thức x+2y ta được 0 + 2.0 = 0 < 200.

=> Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa gốc tọa độ không kể đường thẳng d.

Vậy nếu số phút sử dụng nội mạng là x và ngoại mạng là y mà điểm (x;y) nằm trong miền tam giác OAB không kể đoạn AB thì số tiền phải trả thấp hơn 200 nghìn đồng.

Chú ý

x và y là số tự nhiên nên cần lấy phần không âm của trục Ox và phần không âm của trục Oy.