Giải bài 9 trang 79 SGK Toán 10 tập 1 – Chân trời sáng tạo

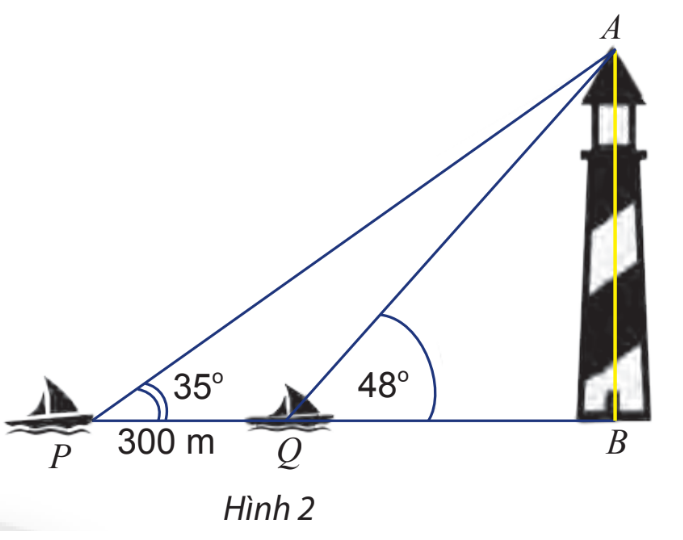
Hai chiếc tàu thủy P và Q cách nhau 300m và thẳng hàng với chân B của tháp hải đăng AB ở trên bờ biển (Hình 2). Từ P và Q, người ta nhìn thấy tháp hải đăng AB dưới các góc

Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Đề bài

Hai chiếc tàu thủy P và Q cách nhau 300m và thẳng hàng với chân B của tháp hải đăng AB ở trên bờ biển (Hình 2). Từ P và Q, người ta nhìn thấy tháp hải đăng AB dưới các góc \(\widehat {BPA} = {35^o}\) và \(\widehat {BQA} = {48^o}.\) Tính chiều cao của tháp hải đăng đó.

Phương pháp giải - Xem chi tiết

Bước 1: Tính AB theo QB, dựa vào tan góc P và Q.

Bước 2: Lập phương trình, tìm QB.

Bước 3: Tính AB: \(AB = QB.\tan {48^ \circ }\)

Lời giải chi tiết

Xét tam giác APB và AQB, ta có:

\(\tan {35^ \circ } = \frac{{AB}}{{PB}} = \frac{{AB}}{{300 + QB}}\) và \(\tan {48^ \circ } = \frac{{AB}}{{QB}}\)

\(\begin{array}{l} \Rightarrow AB = \tan {35^ \circ }.\left( {300 + QB} \right) = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 + \tan {35^ \circ }.QB = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 = \left( {\tan {{48}^ \circ } - \tan {{35}^ \circ }} \right).QB\\ \Leftrightarrow QB = \frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}}\end{array}\)

Mà \(AB = \tan {48^ \circ }.QB\)

\( \Rightarrow AB = \tan {48^ \circ }.\frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}} \approx 568,5\;(m)\)

Vậy tháp hải đăng cao khoảng 568,5 m.

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 7 phiếu

Bài tiếp theo

Giải bài 10 trang 79 SGK Toán 10 tập 1 – Chân trời sáng tạo
Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2m. Gọi D là đỉnh tháp và hai điểm
Giải bài 8 trang 79 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ tinh đến A và B là
Giải bài 7 trang 79 SGK Toán 10 tập 1 – Chân trời sáng tạo
Cho tam giác ABC. Chứng minh rằng:
Giải bài 6 trang 79 SGK Toán 10 tập 1 – Chân trời sáng tạo
Cho tam giác ABC có a = 15,b = 20,c = 25. a) Tính diện tích tam giác ABC b) Tính bán kính đường tròn ngoại tiếp tam giác ABC
Giải bài 5 trang 79 SGK Toán 10 tập 1 – Chân trời sáng tạo
Cho hình bình hành ABCD a) Chứng minh b) Cho AB = 4,BC = 5,BD = 7 Tính AC.
Giải bài 4 trang 79 SGK Toán 10 tập 1 – Chân trời sáng tạo
Cho tam giác ABC có A = 120,b = 8,c = 5. Tính: a) Cạnh a và các góc B, C b) Diện tích tam giác ABC c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.
Giải bài 3 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo
Cho tam giác ABC có a = 8,b = 10,c = 13. Tính các góc A, B, C
Giải bài 2 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo
Cho tam giác ABC. Biết a = 24,b = 13,c = 15. Tính các góc A, B, C
Giải bài 1 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo
Cho tam giác ABC. Biết a = 49,4;b = 26,4;C = 47'20'.Tính hai góc A, B và cạnh c.