Giải bài 8 trang 100 SGK Toán 10 tập 1 – Cánh diều

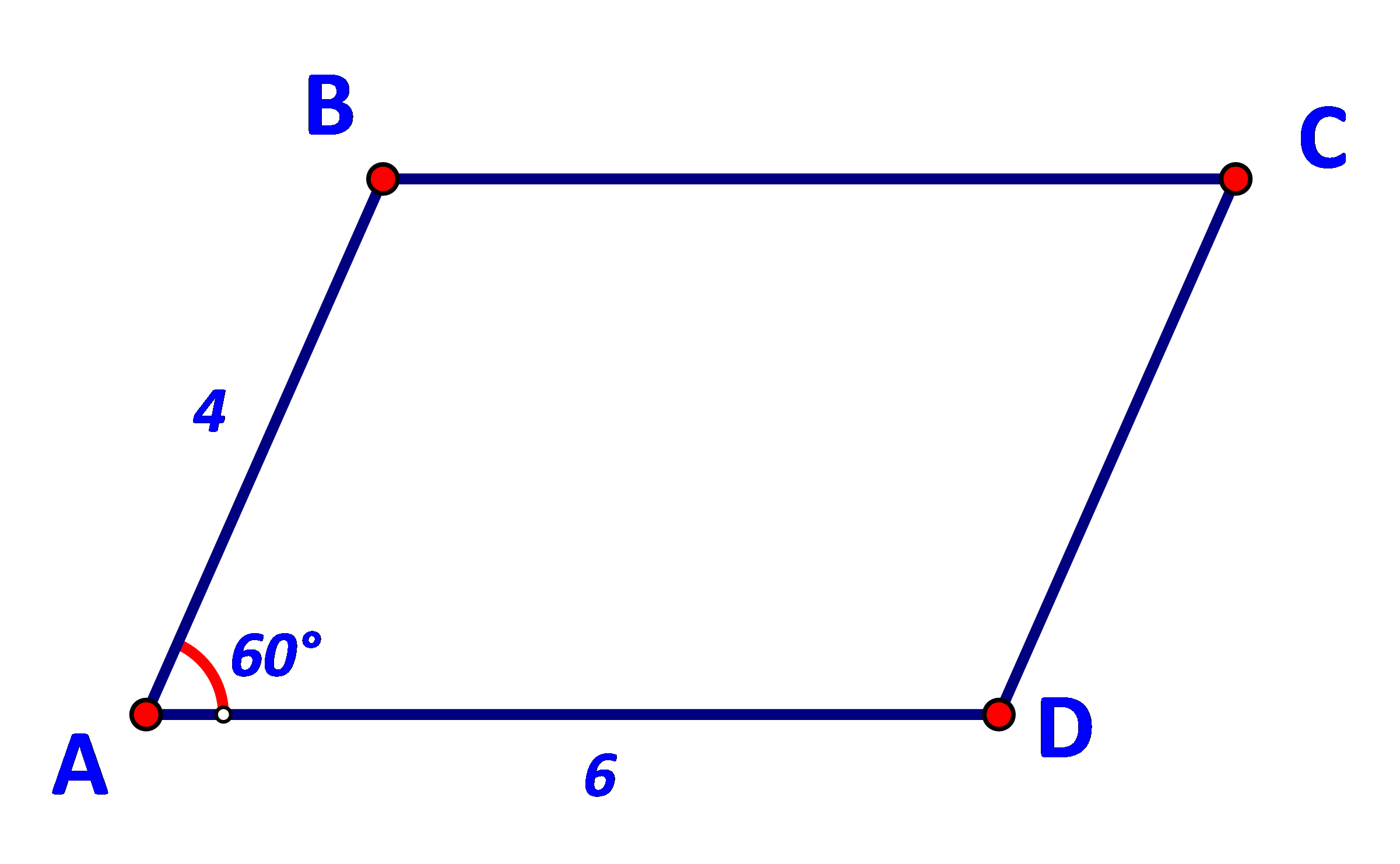
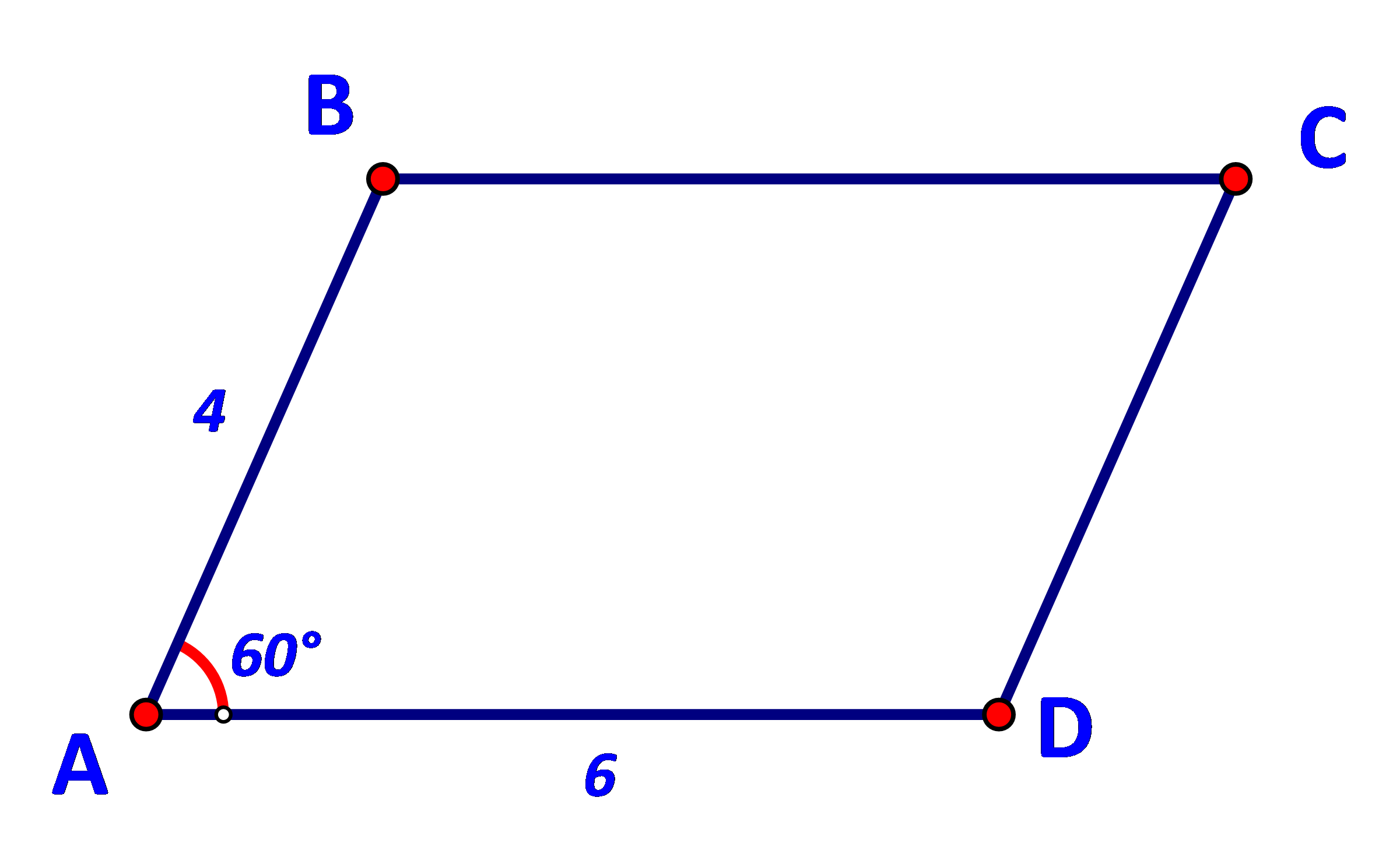
Cho hình bình hành ABCD có AB = 4, AD = 6, BAD =60 (Hình 74).

Đề bài

Cho hình bình hành ABCD có AB = 4, AD = 6, \(\widehat {BAD} = {60^o}\) (Hình 74).

a) Biểu thị các vecto \(\overrightarrow {BD} ,\overrightarrow {AC} \) theo \(\overrightarrow {AB} ,\overrightarrow {AD} \).

b) Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AD} ,\;\overrightarrow {AB} .\overrightarrow {AC} ,\;\overrightarrow {BD} .\overrightarrow {AC} \).

c) Tính độ dài các đường chéo \(BD,AC\).

Phương pháp giải - Xem chi tiết

+) ABCD là hình bình hành thì \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)

+) Tính \(\overrightarrow {AB} .\overrightarrow {AD} \) bằng công thức \(\overrightarrow {AB} .\overrightarrow {AD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos (\overrightarrow {AB} ,\overrightarrow {AD} )\).

\(\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} )\) (tính chất phân phối).

+) Tính BD, AC bởi định lí cosin: \(B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\).

Lời giải chi tiết

a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB}\), \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).

b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)

\(\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) \)

\(= {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28\).

\(\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} )\)

\(= {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20\).

c) Áp dụng định lí cosin cho tam giác ABD ta có:

\(B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\)

\(\Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\)

\(\Leftrightarrow BD = 2\sqrt 7\).

Áp dụng định lí cosin cho tam giác ABC ta có:

\(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\)

\(\Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\)

\(\Leftrightarrow AC = 2\sqrt {19} \).

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4 trên 10 phiếu

Bài tiếp theo

Giải bài 9 trang 100 SGK Toán 10 tập 1 – Cánh diều
Hai lực F1 ,F2 cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc
Giải bài 7 trang 100 SGK Toán 10 tập 1 – Cánh diều
Chứng minh: a) Nếu ABCD là hình bình hành thì
Giải bài 6 trang 100 SGK Toán 10 tập 1 – Cánh diều
Để đo khoảng cách giữa hai vị trí M, N ở hai phía ốc đảo, người ta chọn vị trí O bên ngoài ốc đảo sao cho: O không thuộc đường thẳng MN, các khoảng cách OM, ON và góc MON là đo được (Hình 73).
Giải bài 5 trang 99 SGK Toán 10 tập 1 – Cánh diều
Một người đứng ở bờ sông, muốn đo độ rộng của khúc sông chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ sông song song với nhau.)
Giải bài 4 trang 99 SGK Toán 10 tập 1 – Cánh diều
Có hai trạm quan sát A và B ven hồ và một trạm quan sát C ở giữa hồ. Để tính khoảng cách từ A và B đến C, người ta làm như sau:
Giải bài 3 trang 99 SGK Toán 10 tập 1 – Cánh diều
Không dùng thước đo góc, làm thế nào để biết số đo góc đó. Ban Hoài vẽ góc xOy và đó bạn Đông làm thế nào có thể biết được số đo của góc này khi không có thước đo góc. Bạn Đông làm như sau:
Giải bài 2 trang 99 SGK Toán 10 tập 1 – Cánh diều
Không dùng máy tính cầm tay, hãy tính giá trị của các biểu thức sau:
Giải bài 1 trang 99 SGK Toán 10 tập 1 – Cánh diều
a) Độ dài cạnh BC và độ lớn góc B. b) Bán kính đường tròn ngoại tiếp c) Diện tích của tam giác d) Độ dài đường cao xuất phát từ A