Toán 7, giải toán lớp 7 chân trời sáng tạo Bài 2. Tia phân giác trang 73 SGK Toán 7 chân trời sáng..

Giải bài 5 trang 75 SGK Toán 7 tập 1 - Chân trời sáng tạo


Vẽ hai góc kề bù ..

Đề bài

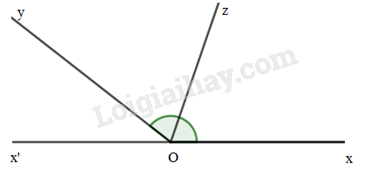
Vẽ hai góc kề bù \(\widehat {xOy},\widehat {yOx'}\), biết \(\widehat {xOy} = 142^\circ \). Gọi Oz là tia phân giác của \(\widehat {xOy}\). Tính \(\widehat {x'Oz}\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+ Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)

+ Hai góc kề bù có tổng số đo là 180 độ

Lời giải chi tiết

Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.142^\circ  = 71^\circ \)

Mà \(\widehat {x'Oz}\) và \(\widehat {xOz}\) là 2 góc kề bù nên \(\widehat {xOz} + \widehat {x'Oz} = 180^\circ\) hay \(71^\circ  + \widehat {x'Oz} = 180^\circ\) suy ra \(\widehat {x'Oz} = 180^\circ  - 71^\circ  = 109^\circ \)

Vậy \(\widehat {x'Oz} = 109^\circ \)


Bình chọn:
4.7 trên 30 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store