Giải bài 1 trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo

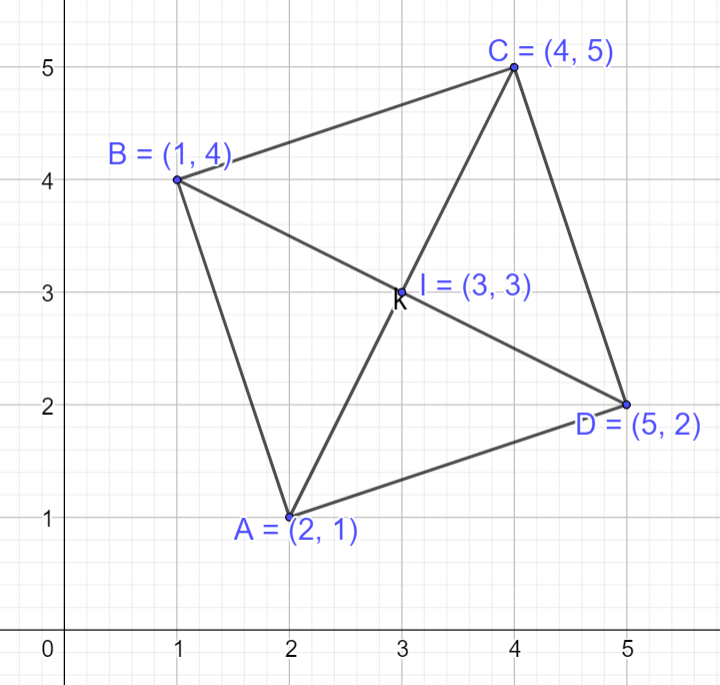
Trong mặt phẳng Oxy, cho bốn điểm A(2;1),B(1;4),C(4;5),D(5;2) a) Chứng minh ABCD là một hình vuông b) Tìm tọa độ tâm I của hình vuông ABCD

Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Đề bài

Trong mặt phẳng Oxy, cho bốn điểm $A(2;1),B(1;4),C(4;5),D(5;2)$

a) Chứng minh ABCD là một hình vuông

b) Tìm tọa độ tâm I của hình vuông ABCD

Phương pháp giải - Xem chi tiết

a) Bước 1: Tính AB, BC, CD, DA (Chứng minh AB=BC=CD=DA)

Bước 2: Chứng minh $AB \bot BC$ thông qua tích vô hướng

b) Sử dụng tính chất trung điểm $M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)$ với M là trung điểm của AB

Lời giải chi tiết

a) Ta có: $\overrightarrow {AB} = ( - 1;3),\overrightarrow {BC} = (3;1),\overrightarrow {CD} = (1; - 3),\overrightarrow {DA} = ( - 3; - 1)$

Suy ra $AB = BC = CD = DA = \sqrt {10}$

Mặt khác $\overrightarrow {AB} .\overrightarrow {BC} = ( - 1).3 + 3.1 = 0 \Rightarrow AB \bot BC$

Vậy ABCD là hình vuông

b) Ta có ABCD là hình vuông, nên tâm I là trung điểm của đoạn thẳng AC

Vậy tọa độ điểm I là $I(3;3)$

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 6 phiếu

Bài tiếp theo

Giải bài 2 trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo
Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O) .Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ mặt phẳng để chứng minh EF vuông góc với DB
Giải bài 3 trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo
Tìm tọa độ giao điểm và góc giữa hai đường thẳng d1 và d2 trong mỗi trường hợp sau:
Giải bài 4 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Tính bán kính của đường tròn tâm M( - 2;3) và tiếp xúc với đường thẳng d:14x - 5y + 60 = 0
Giải bài 5 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Tính khoảng cách giữa hai đường thẳng
Giải bài 6 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Tìm tâm và bán kính của các đường tròn có phương trình:
Giải bài 7 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Lập phương trình đường tròn trong các trường hợp sau:
Giải bài 8 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Viết phương trình tiếp tuyến của đường tròn
Giải bài 9 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip sau:
Giải bài 10 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Viết phương trình chính tắc của elip thỏa mãn từng điều kiện:
Giải bài 11 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol sau:
Giải bài 12 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Viết phương trình chính tắc của hypebol thỏa mãn từng điều kiện sau:
Giải bài 13 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:
Giải bài 14 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Viết phương trình chính tắc của parabol thỏa mãn từng điều kiện sau:
Giải bài 15 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một gương lõm có mặt cắt hình parabol như hình 1, có tiêu điểm cách đỉnh 5 cm. Cho biết bề sâu của gương là 45 cm. Tính khoảng cách AB
Giải bài 16 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol (hình 2). Nước sẽ chảy thông qua một đường ống nằm ở tiêu điểm của parabol
Giải bài 17 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạo
Cổng trời của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc kẻ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng
Giải bài 18 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một người đứng giữa một tấm ván gỗ đặt trên một giàn giáo để sơn tường nhà. Biết rằng dàn giáo dài 16m và độ võng tại tâm của ván gỗ (điểm ở giữa của ván gỗ) là 3 cm (hình 4). Cho biết đường cong của ván gỗ có hình parabol

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.