Đề kiểm tra 15 phút - Đề số 1 - Bài 7, 8 - Chương 2 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 7, 8 - Chương 2 - Hình học 7
Đề bài
Bài 1. Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC, biết AB = 20cm, AH = 12cm, AC = 15cm. Tính BC, BH, CH.
Bài 2. Các tam giác cho dưới đây có phải là tam giác vuông không? Hãy chứng minh, nếu là tam giác vuông cho biết vuông tại đỉnh nào?
a) \(AB = 8cm;\,AC = 17cm;\,BC = 15cm.\)
b) \(AB = 25cm;\,AC = 24cm;\,BC = 6cm.\)
Phương pháp giải - Xem chi tiết
Sử dụng định lý Py-ta-go thuận và đảo
Lời giải chi tiết
Bài 1.
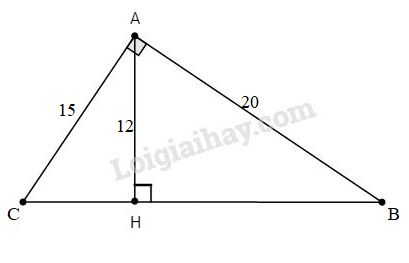
\(\Delta ABC\) vuông tại A ta có \(B{C^2} = A{B^2} + A{C^2}\) (định lý Pytago)
\(\eqalign{ & = {20^2} + {15^2} \cr & = 625 \cr} \)
\( \Rightarrow B{C^2} = \sqrt {625} = 25\,(cm)\)
Lại có \(AH \bot BC\) (giả thiết) nên \(\Delta AHB\) vuông tại H.
Ta có \(B{H^2} = A{B^2} - A{H^2}\) (định lý Pytago)
\(\, = {20^2} - {12^2} = 256\)
\( \Rightarrow BH = \sqrt {256} = 16\,(cm)\)
Do đó \(CH = BC - BH= 25 - 16 = 9\,(cm)\)
Bài 2.
a) Ta có \({8^2} + {15^2} = {17^2}\,(A{B^2} + B{C^2} = C{A^2})\). Theo định lí Pytago đảo ta có \(\Delta ABC\) vuông tại B.
b) Ta có \({6^2} + {24^2} \ne {25^2}\).
Vậy \(\Delta ABC\) không phải là tam giác vuông.
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 2 - Bài 7, 8 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 7, 8 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 7, 8 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 5 - Bài 7, 8 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 7 - Bài 7, 8 - Chương 2 - Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
