 Giải bài tập vật lý 9, Vật lý lớp 9 - Để học tốt vật lý 9
Giải bài tập vật lý 9, Vật lý lớp 9 - Để học tốt vật lý 9
 Bài 45. Ảnh của một vật tạo bởi thấu kính phân kì
Bài 45. Ảnh của một vật tạo bởi thấu kính phân kì
Bài C7 trang 123 SGK Vật lí 9
Vận dụng kiến thức hình học, tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh...
Đề bài
Vận dụng kiến thức hình học, tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh trong hai trường hợp ở C5 khi vật có chiều cao h = 6mm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào tỷ số đồng dạng của hai tam giác đồng dạng.
Lời giải chi tiết
Trường hợp 1- thấu kính hội tụ
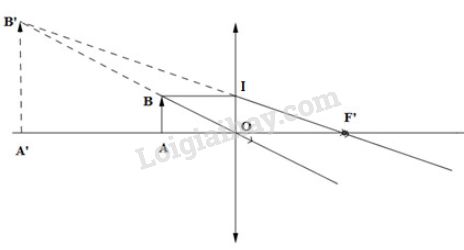
+ Ta có: \(\Delta BB'I \sim \Delta OB'F'\)
Ta suy ra: \(\dfrac{{BI}}{{OF'}} = \dfrac{{BB'}}{{OB'}}\) (1)
Theo đề bài, ta có: \(OA = BI = 8cm\), \(OF' = 12cm\)
Lại có: \(OB' = OB + BB'\)
Ta suy ra \(\left( 1 \right) \Leftrightarrow \dfrac{8}{{12}} = \dfrac{{BB'}}{{OB + BB'}}\)
\(\begin{array}{l} \Rightarrow \dfrac{{12}}{8} = \dfrac{{OB + BB'}}{{BB'}}\\ \Rightarrow 1,5 = \dfrac{{OB}}{{BB'}} + 1\end{array}\)
\( \Rightarrow \dfrac{{OB}}{{BB'}} = 0,5 \Rightarrow \dfrac{{BB'}}{{OB}} = 2\) (2)
+ Ta có: \(\Delta OA'B' \sim \Delta OAB\)
Ta suy ra: \(\dfrac{{OA'}}{{OA}} = \dfrac{{A'B'}}{{AB}} = \dfrac{{OB'}}{{OB}}\) (3)
Ta có \(OB' = OB + BB'\)
Ta suy ra \(\left( 3 \right) \Leftrightarrow \dfrac{{OA'}}{{OA}} = \dfrac{{A'B'}}{{AB}} = \dfrac{{OB + BB'}}{{OB}} = 1 + \dfrac{{BB'}}{{OB}}\)
Thế (2) vào (3) ta được: \(\dfrac{{OA'}}{{OA}} = \dfrac{{A'B'}}{{AB}} = 1 + 2 = 3\)
Từ đây ta suy ra:
- Khoảng cách từ ảnh đến thấu kính: \(OA' = 3.OA = 3.8 = 24cm\)
- Chiều cao của ảnh: \(A'B' = 3.AB = 3.6 = 18mm\)
Vậy ảnh có chiều cao \(18mm\) (cao gấp 3 lần vật) cách thấu kính một khoảng là \(24cm\)
+ Trường hợp 2: Thấu kính phân kì
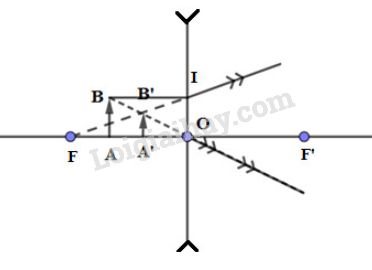
+ Ta có: \(\Delta IB'B \sim \Delta FB'O\)
Ta suy ra: \(\dfrac{{IB}}{{FO}} = \dfrac{{B'B}}{{B'O}}\)
Theo đầu bài ta có: \(IB = AO = 8cm\) và \(FO = 12cm\)
Ta suy ra: \(\dfrac{8}{{12}} = \dfrac{{B'B}}{{B'O}} \Rightarrow \dfrac{{B'B}}{{B'O}} = \dfrac{2}{3}\) (1)
+ Ta có: \(\Delta OAB \sim \Delta OA'B'\)
Ta suy ra: \(\dfrac{{OA}}{{OA'}} = \dfrac{{OB}}{{OB'}} = \dfrac{{AB}}{{A'B'}}\)
Lại có: \(OB = OB' + BB'\)
Ta suy ra: \(\dfrac{{OA}}{{OA'}} = \dfrac{{AB}}{{A'B'}} = \dfrac{{OB' + BB'}}{{OB'}} = 1 + \dfrac{{BB'}}{{OB'}}\) (2)
Từ (1) và (2) ta suy ra: \(\dfrac{{OA}}{{OA'}} = \dfrac{{AB}}{{A'B'}} = 1 + \dfrac{2}{3} = \dfrac{5}{3}\)
Từ đây, ta suy ra:
- Khoảng cách từ ảnh đến thấu kính: \(OA' = \dfrac{{OA}}{{\dfrac{5}{3}}} = \dfrac{8}{{\dfrac{5}{3}}} = 4,8cm\)
- Chiều cao của ảnh: \(A'B' = \dfrac{{AB}}{{\dfrac{5}{3}}} = \dfrac{6}{{\dfrac{5}{3}}} = 3,6mm\)
Vậy, ảnh có chiều cao \(3,6mm\) (cao gấp \(0,6\) lần vật) và cách thấu kính một khoảng là \(4,8cm\)
Loigiaihay.com
Các bài khác cùng chuyên mục
- STEM - Thấu kính thần kì khi nhìn qua cốc nước
- Giải đề thi học kì 2 lý lớp 9 năm 2020 - 2021 trường THCS Gia Thụy
- Giải đề thi học kì 2 lý lớp 9 năm 2020 - 2021 Phòng GD - ĐT Thành Phố Thủ Dầu Một
- Đề số 4 - Đề kiểm tra học kì 2 - Vật lí 9
- Đề kiểm tra giữa học kì 2 Vật lí 9 - Đề số 03 có lời giải chi tiết
- STEM - Thấu kính thần kì khi nhìn qua cốc nước
- Giải đề thi học kì 2 lý lớp 9 năm 2020 - 2021 trường THCS Gia Thụy
- Giải đề thi học kì 2 lý lớp 9 năm 2020 - 2021 Phòng GD - ĐT Thành Phố Thủ Dầu Một
- Đề số 4 - Đề kiểm tra học kì 2 - Vật lí 9
- Đề kiểm tra giữa học kì 2 Vật lí 9 - Đề số 03 có lời giải chi tiết












Danh sách bình luận