Hàm số. Cách cho một hàm số
Nếu với mỗi giá trị \(x\) thuộc tập D, ta xác định được một và chỉ một giá trị tương ứng thuộc tập hợp số thực \(\mathbb{R}\) thì ta có một hàm số.
1. Lý thuyết
+ Định nghĩa:
Nếu với mỗi giá trị \(x\) thuộc tập D, ta xác định được một và chỉ một giá trị tương ứng thuộc tập hợp số thực \(\mathbb{R}\) thì ta có một hàm số.
\( \Rightarrow \) Nếu với một giá trị của x mà ta tìm được từ 2 giá trị của y thì y không là hàm số của x.
+ Cách gọi: \(x\) là biến số, \(y\) là hàm số của \(x\).
+ Kí hiệu: Thường dùng \(y = f(x)\)
+ Cách cho một hàm số
Dạng bảng
Ví dụ: Dự báo thời tiết ngày 2/11/2022 tại Hà Nội
|
Giờ |
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
|
Nhiệt độ \({(^o}C)\) |
19 |
17 |
22 |
26 |
29 |
27 |
25 |
23 |
Dạng biểu đồ
Ví dụ: Dự báo thời tiết ngày 20/11/2021 tại Hà Nội
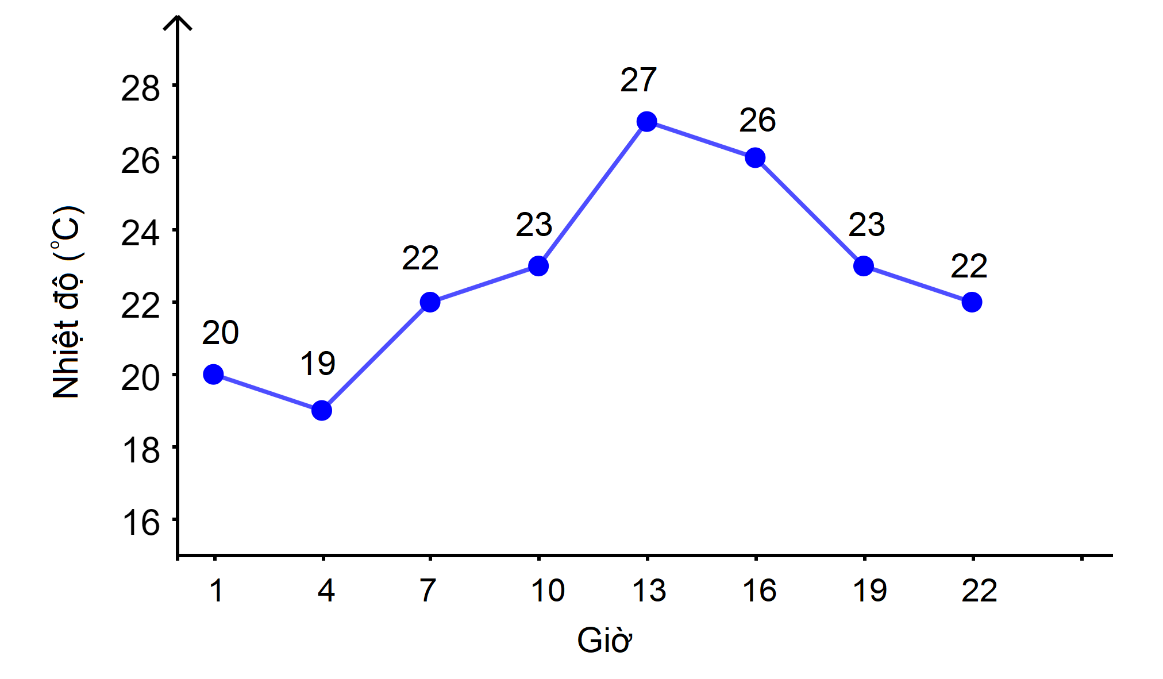
Dạng công thức
Một hàm số có thể được cho bởi một hoặc nhiều công thức.
Chẳng hạn:
\(y = {x^2} + 3\)
\(f(x) = \left\{ \begin{array}{l} - 3x + 5\quad \quad x \le 1\\2{x^2}\quad \quad \quad \;\;x > 1\end{array} \right.\)
2. Ví dụ minh họa
+ Hàm số
1. Bảng dưới đây biểu thị một hàm số
|
\(t\) (giây) |
1 |
2 |
4 |
6 |
9 |
|
\(v\) (mét/giây) |
2 |
3 |
0 |
5,5 |
7 |
\(v\) là một hàm số của \(t\) vì ứng với mỗi giá trị của t, có một và chỉ một giá trị tương ứng của v.
2. Hàm số cho bởi công thức
\(y = \sqrt x + 4\) với \(x \ge 0\)
\(f(x) = \left\{ \begin{array}{l}1\quad \quad \quad \;\;\quad \quad x \le 0\\2x - 1\quad \quad \quad 0 < x \le 5\\{x^2} - 3x - 1\quad \quad x > 5\end{array} \right.\)
+ Không là hàm số
a) Cho bảng sau
|
\(x\) |
1 |
0 |
2 |
1 |
5 |
|
\(y\) |
2 |
3 |
0 |
-1 |
7 |
\(y\) không là hàm số của \(x\) vì với \(x = 1\) ta xác định được hai giá trị của y là \(y = 2\) và \(y = - 1\).
b) Cho \(x,y \in \mathbb{R}\) thỏa mãn: \({x^2} + {y^2} = 4\)
Khi đó \(y\) không là hàm số của \(x\) vì với \(x = 0\) ta xác định được hai giá trị \(y = 2\) và \(y = - 2\) đều thỏa mãn.
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
