 Toán 10, giải toán lớp 10 chân trời sáng tạo
Toán 10, giải toán lớp 10 chân trời sáng tạo
 Bài 3. Đường tròn trong mặt phẳng tọa độ Toán 10 Chân ..
Bài 3. Đường tròn trong mặt phẳng tọa độ Toán 10 Chân ..
Giải mục 2 trang 61, 62 SGK Toán 10 tập 2 - Chân trời sáng tạo
Viết phương trình tiếp tuyến của đường tròn (C) tại điểm A(4;6) Một vận động viên ném đĩa đã vung đĩa theo một đường tròn (C) có phương trình:
HĐ Khám phá 2
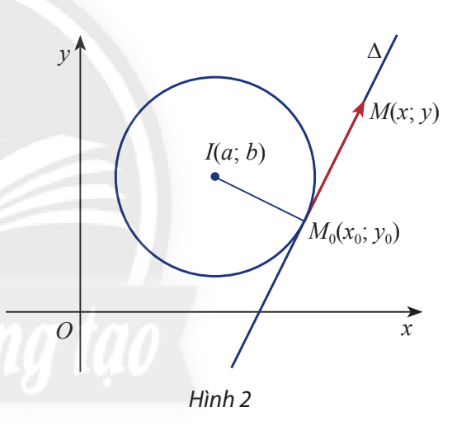
Cho điểm \({M_0}\left( {{x_0};{y_0}} \right)\) nằm trên đường tròn \((C)\) tâm \(I(a;b)\)và cho điểm \(M(x;y)\) tùy ý trong mặt phẳng Oxy. Gọi \(\Delta \) là tiếp tuyến với \((C)\) tại \({M_0}\).
a) Viết biểu thức tọa độ của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \).
b) Viết biểu thức tọa độ của tích vô hướng của hai vecto \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \).
c) Phương trình \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0\) là phương trình của đường thẳng nào?
Phương pháp giải:
a) Với \(A(a;b),B(x;y)\) thì tọa độ của vt \(\overrightarrow {AB} = (x - a;y - b)\).
b) Với \(\overrightarrow a = \left( {a,b} \right),\overrightarrow b = (x;y)\) thì \(\overrightarrow a .\overrightarrow b = ax + by\).
c) Từ tích vô hướng đưa ra kết luận là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\).
Lời giải chi tiết:
a) Biểu thức tọa độ của hai vecto \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \) là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\).
b) Ta có:
\(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = \left( {x - {x_0}} \right)\left( {a - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right)\).
c) \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0 \Rightarrow \overrightarrow {{M_0}M} \bot \overrightarrow {{M_0}I} \)
\({M_0}I\) là đoạn thẳng nối tâm với điểm thuộc đường tròn, suy ra đường thẳng \(M{M_0}\) là tiếp tuyến của đường tròn tại điểm \({M_0}\), hay chính là \(\Delta \).
Thực hành 3
Viết phương trình tiếp tuyến của đường tròn \((C):{x^2} + {y^2} - 2x - 4y - 20 = 0\) tại điểm \(A(4;6)\).
Phương pháp giải:
Phương trình tiếp tuyến của đường tròn tâm \(I(a;b)\) tại điểm \(M({x_0};{y_0})\)nằm trên đường tròn là: \(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\).
Lời giải chi tiết:
Ta có \({4^2} + {6^2} - 2.4 - 4.6 - 20 = 0\), nên điểm A thuộc (C).
Đường tròn \((C):{x^2} + {y^2} - 2x - 4y - 20 = 0\) có tâm \(I(1;2)\).
Phương trình tiếp tuyến d của (C) tại \(A(4;6)\) là:
\(\left( {1 - 4} \right)\left( {x - 4} \right) + \left( {2 - 6} \right)\left( {y - 6} \right) = 0\)
\(\Leftrightarrow 3x + 4y - 36 = 0\).
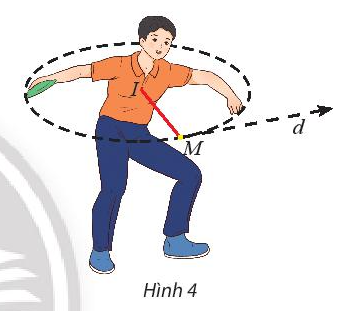
Vận dụng 3
Một vận động viên ném đĩa đã vung đĩa theo một đường tròn \((C)\) có phương trình:
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\).
Khi người đó vung đĩa đến vị trí điểm \(M\left( {\frac{{17}}{{12}};2} \right)\) thì buông đĩa (hình 4). Viết phương trình tiếp tuyến của đường tròn \((C)\) tại điểm M.
Phương pháp giải:
Phương trình tiếp tuyến của đường trong tâm \(I(a;b)\) tại điểm \(M({x_0};{y_0})\) nằm trên đường tròn là: \(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\).
Lời giải chi tiết:
Ta có \({\left( {\frac{{17}}{{12}} - 1} \right)^2} + {\left( {2 - 1} \right)^2} = \frac{{169}}{{144}}\), nên điểm M thuộc (C).
Đường tròn \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\) có tâm \(I(1;1)\).
Phương trình tiếp tuyến d của (C) tại \(M\left( {\frac{{17}}{{12}};2} \right)\) là:
\(\left( {1 - \frac{{17}}{{12}}} \right)\left( {x - \frac{{17}}{{12}}} \right) + \left( {1 - 2} \right)\left( {y - 2} \right) = 0\)
\( \Leftrightarrow - \frac{5}{{12}}x - y + \frac{{373}}{{144}} = 0\)
\( \Leftrightarrow 5x + 12y - \frac{{373}}{{12}} = 0\).
- Giải bài 1 trang 62 SGK Toán 10 tập 2 – Chân trời sáng tạo
- Giải bài 2 trang 62 SGK Toán 10 tập 2 – Chân trời sáng tạo
- Giải bài 3 trang 62 SGK Toán 10 tập 2 – Chân trời sáng tạo
- Giải bài 4 trang 62 SGK Toán 10 tập 2 – Chân trời sáng tạo
- Giải bài 5 trang 63 SGK Toán 10 tập 2 – Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo












Danh sách bình luận