Toán 10, giải toán lớp 10 chân trời sáng tạo Bài 1. Giá trị lượng giác của một góc từ 0 đến 180 Toán..

Giải mục 1 trang 61, 62 SGK Toán 10 tập 1 - Chân trời sáng tạo


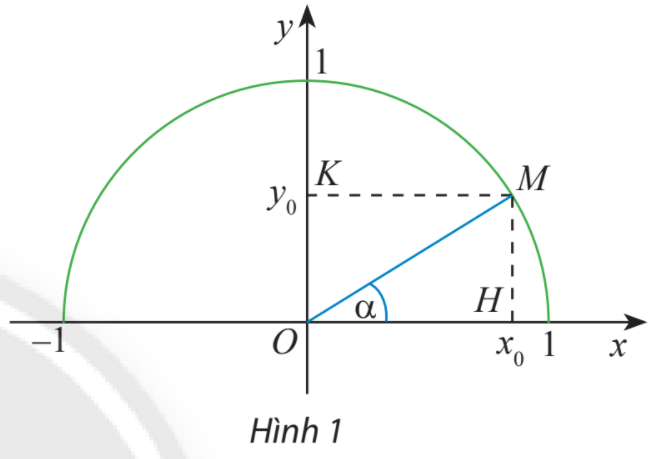
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn Tìm các giá trị lượng giác của góc 135

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Lựa chọn câu để xem lời giải nhanh hơn

HĐ Khám phá 1

Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính \(R = 1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn \(\alpha ,\)lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha .\) Giả sử điểm M có tọa độ \(({x_0};{y_0}).\) Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:

\(\sin \alpha  = {y_0};\;\cos \alpha  = {x_0};\;\tan \alpha  = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha  = \frac{{{x_0}}}{{{y_0}}}.\)

Phương pháp giải:

Tam giác vuông OHM có \(\alpha  = \widehat {xOM}\)

\(\sin \alpha  = \frac{{MH}}{{OM}};\;\cos \alpha  = \frac{{OH}}{{OM}};\;\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}.\)

Lời giải chi tiết:

Ta có: tam giác vuông OHM vuông tại H và \(\alpha  = \widehat {xOM}\)

Do đó: \(\sin \alpha  = \frac{{MH}}{{OM}};\;\cos \alpha  = \frac{{OH}}{{OM}}.\)

Mà \(MH = {y_0};OH = {x_0};OM = 1.\)

\( \Rightarrow \sin \alpha  = \frac{{{y_0}}}{1} = {y_0};\;\cos \alpha  = \frac{{{x_0}}}{1} = {x_0}\;.\)

\( \Rightarrow \tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}.\)

Thực hành 1

Tìm các giá trị lượng giác của góc \({135^o}\)

Phương pháp giải:

Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\)

Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị \(\cos {135^o},\;\sin {135^o}\)

Từ đó suy ra\(\;\tan {135^o} = \frac{{\sin {{135}^o}}}{{\cos {{135}^o}}},\;\;\cot {135^o} = \frac{{\cos {{135}^o}}}{{\sin {{135}^o}}}.\)

Lời giải chi tiết:

Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\), H là hình chiếu vuông góc của M trên Oy.

 

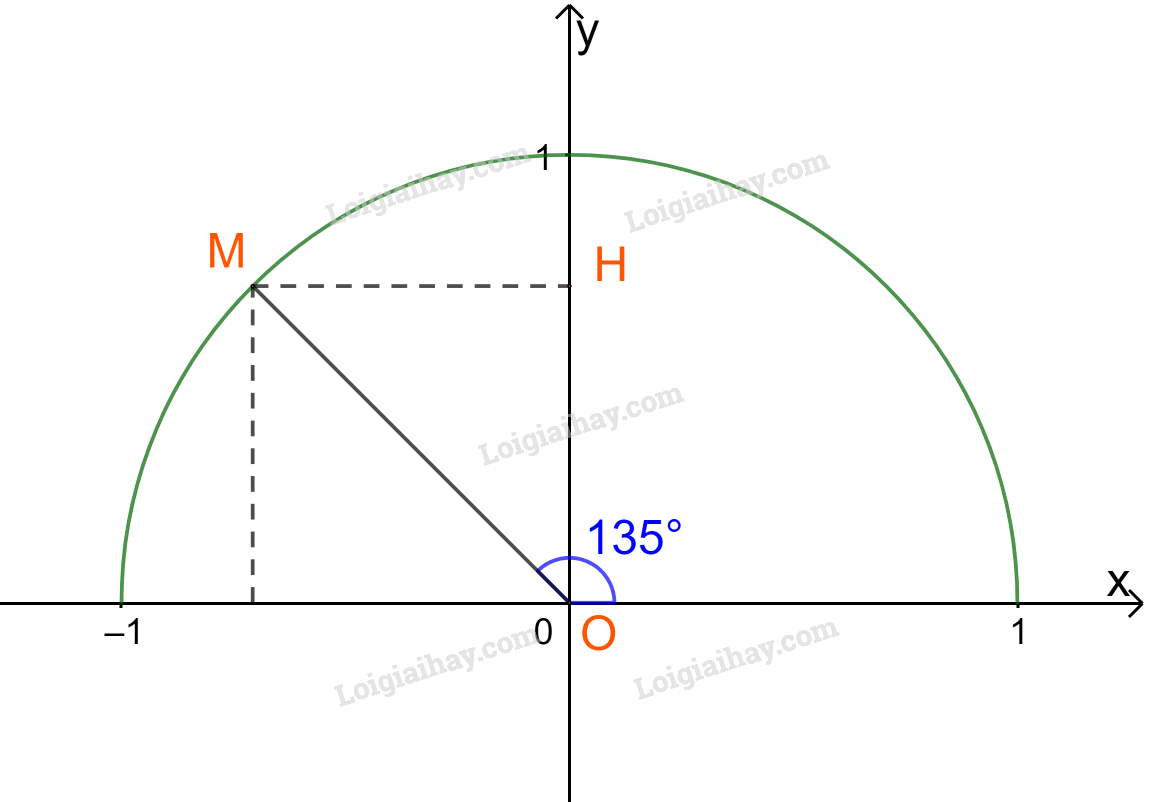
Ta có: \(\widehat {MOy} = {135^o} - {90^o} = {45^o}\).

Tam giác OMH vuông cân tại H nên \(OH = MH = \frac{{OM}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.\)

Vậy tọa độ điểm M là \(\left( { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right).\)

Vậy theo định nghĩa ta có:

 \(\begin{array}{l}\;\sin {135^o} = \frac{{\sqrt 2 }}{2};\;\;\cos {135^o} =  - \frac{{\sqrt 2 }}{2};\\\;\tan {135^o} =  - 1;\;\;\cot {135^o} =  - 1.\end{array}\)

Chú ý

Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({135^o}\)

Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:

Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)

Tính \(\sin {135^o}\), bấm phím:  sin  1  3  5  \(^o\)’’’  = ta được kết quả là \(\frac{{\sqrt 2 }}{2}\)

Tính \(\cos {135^o}\),bấm phím:  cos  1  3  5  \(^o\)’’’  = ta được kết quả là \(\frac{{ - \sqrt 2 }}{2}\)

Tính \(\tan {135^o}\), bấm phím:  tan  1  3  5  \(^o\)’’’  = ta được kết quả là \( - 1\)

(Để tính \(\cot {135^o}\), ta tính \(1:\tan {135^o}\))


Bình chọn:
4.3 trên 4 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store