-
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
SBT Toán 11 - giải SBT Toán 11 - Kết nối tri thức với cuộc sống
Bài tập cuối chương VII - SBT Toán 11 KNTT
Giải bài 7.47 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình chóp \(S.ABCD\)có tất cả các cạnh đều bằng \(a\), gọi \(O\)là giao điểm của \(AC\) và \(BD\).
Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh
Đề bài
Cho hình chóp \(S.ABCD\)có tất cả các cạnh đều bằng \(a\), gọi \(O\)là giao điểm của \(AC\) và \(BD\). Khoảng cách giữa hai đường thẳng \(AB\) và \(SD\) bằng
A. \(\frac{{a\sqrt 6 }}{3}\).
B. \(\frac{{a\sqrt 3 }}{2}\).
C. .\(\frac{{a\sqrt 6 }}{3}\).
D. \(\frac{{a\sqrt 6 }}{2}\).
Phương pháp giải - Xem chi tiết
Gọi \(M,N\) lần lượt là trung điểm của các cạnh\(AB,CD\); \(H\) là hình chiếu vuông góc của \(O\) trên \(SN.\)
Vì \(AB{\rm{//}}CD\) nên\(d\left( {AB,SD} \right) = d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\)
Ta có \(\left\{ \begin{array}{l}CD \bot SO\\CD \bot ON\end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH\)
Khi đó \(\left\{ \begin{array}{l}CD \bot OH\\OH \bot SN\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.\)
Tam giác \(SOD\) vuông tại \(O\) nên \(O{S^2} = S{D^2} - O{D^2}\)
Tam giác \(SON\) vuông tại \(O\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{N^2}}} + \frac{1}{{O{S^2}}} \Rightarrow OH\)
Vậy \(d\left( {AB,SD} \right) = 2OH\).
Lời giải chi tiết
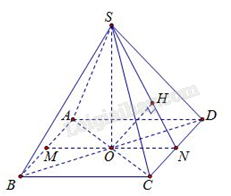
Gọi \(M,N\) lần lượt là trung điểm của các cạnh\(AB,CD\); \(H\) là hình chiếu vuông góc của \(O\) trên \(SN.\)
Vì \(AB{\rm{//}}CD\) nên \(d\left( {AB,SD} \right) = d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\)
Ta có \(\left\{ \begin{array}{l}CD \bot SO\\CD \bot ON\end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH\)
Khi đó \(\left\{ \begin{array}{l}CD \bot OH\\OH \bot SN\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.\)
Tam giác \(SOD\) vuông tại \(O\) nên \(O{S^2} = S{D^2} - O{D^2} = {a^2} - {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = \frac{{{a^2}}}{2}\)
Tam giác \(SON\) vuông tại \(O\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{N^2}}} + \frac{1}{{O{S^2}}} = \frac{1}{{\frac{{{a^2}}}{4}}} + \frac{1}{{\frac{{{a^2}}}{2}}} = \frac{6}{{{a^2}}} \Rightarrow OH = \frac{a}{{\sqrt 6 }} = \frac{{a\sqrt 6 }}{6}\)
Vậy \(d\left( {AB,SD} \right) = 2OH = \frac{{a\sqrt 6 }}{3}\).
Bình luận
Chia sẻ
- Giải bài 7.48 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 7.49 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 7.50 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 7.51 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 7.52 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Giải bài 43 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 39 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 40 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 41 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 42 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 43 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 42 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 41 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 40 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 39 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
