Giải bài 7 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo

Một chú cá heo nhảy lên khỏi mặt nước sau t giây được cho bởi hàm số

Đề bài

Một chú cá heo nhảy lên khỏi mặt nước sau t giây được cho bởi hàm số $h\left( t \right) = - 4,9{t^2} + 9,6t$ .

Tính khoảng thời gian cá heo ở trên không.

Phương pháp giải - Xem chi tiết

Bước 1: Từ giả thiết lập bất phương trình.

Bước 2: Giải bất phương trình vừa tìm được.

Lời giải chi tiết

Khoảng thời gian cá heo ở trên không (cao hơn mặt nước) chính là khoảng t để h(t) > 0.

Ta có bất phương trình $h\left( t \right) > 0 \Leftrightarrow - 4,9{t^2} + 9,6t > 0$ .

Xét tam thức $f\left( t \right) = - 4,9{t^2} + 9,6t$ có $\Delta = 92.16 > 0$ , có hai nghiệm phân biệt là ${x_1} = 0,{x_2} = \frac{{96}}{{49}}$ và có $a = - 4,9 < 0$ .

Ta có bảng xét dấu như sau:

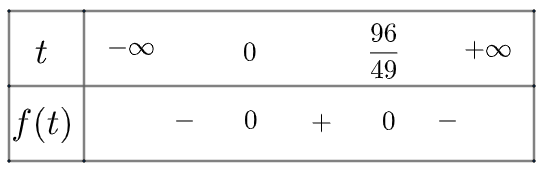
Vậy khoảng thời gian cá heo ở trên không là khoảng $\left( {0;\frac{{96}}{{49}}} \right)$ giây.

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 12 phiếu

Bài tiếp theo

Giải bài 8 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo
với đơn vị tính bằng nghìn đồng. Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng nào?
Giải bài 9 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo
Để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới bao xa? Làm tròn kết quả đến hàng phần mười
Giải bài 6 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một quả bóng được bắn thẳng lên từ độ cao 2 m với vận tốc ban đầu là 30 m/s. Khoảng cách quả bóng so với mặt đất t giây được cho bởi hàm số:
Giải bài 5 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một tam giác vuông có một cạnh góc vuông ngắn hơn cạnh huyền 8 cm. Tính độ dài của cạnh huyền, biết chu vi của tam giác bằng 30 cm.
Giải bài 4 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo
Giải các phương trình sau
Giải bài 3 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo
Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau
Giải bài 2 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo
Giải các bất phương trình sau
Giải bài 1 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo
Xét dấu của các tam thức bậc hai sau

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.