Giải bài 4.5 trang 50 SGK Toán 10 tập 1 – Kết nối tri thức

Trên mặt phẳng tọa độ Oxy hãy vẽ các vecto OA, MN với A (1; 2), M (0; -1), N (3; 5).

Đề bài

Trên mặt phẳng tọa độ Oxy hãy vẽ các vecto \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) với A (1; 2), M (0; -1), N (3; 5).

a) Chỉ ra mỗi quan hệ giữa hai vecto trên.

b) Một vật thể khởi hành từ M chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn vởi vecto \(\overrightarrow v = \overrightarrow {OA} \). Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu sẽ tới N?

Lời giải chi tiết

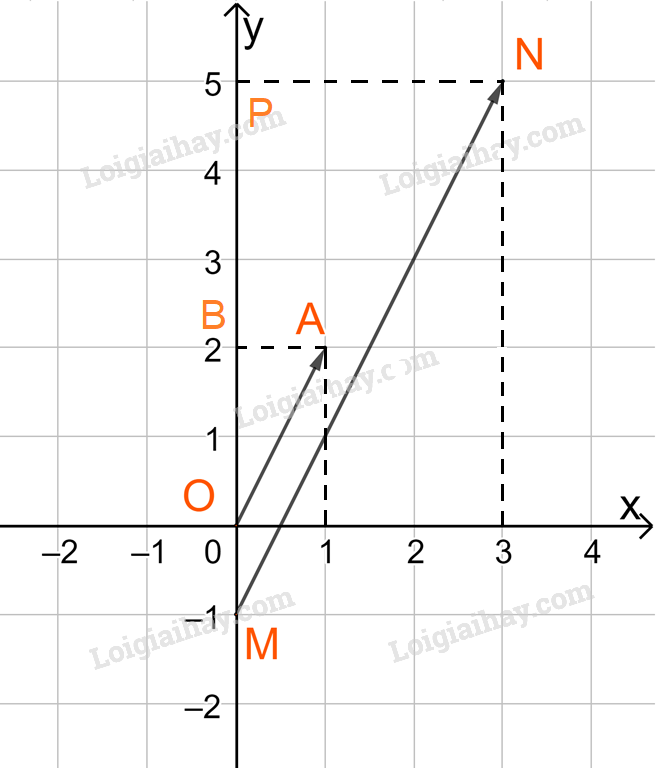
Lấy điểm B(0;2) và P(0;5).

Ta có: OB=2, AB =1, MP=6 và PN=3.

Xét hai tam giác vuông OBA và MPN ta có: \(\frac{{OB}}{{MP}} = \frac{{AB}}{{PN}} = \frac{1}{3}\)

Do đó hai tam giác đồng dạng và OA // MN.

Suy ra \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng phương.

Hơn nữa, \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng hướng và MN = 3 OA.

b) Mỗi giờ, vật thể đó đi được quãng đường tương ứng với đoạn thẳng OA.

Vì \({MN} = 3. {OA} \) nên vật thể đó sẽ đi qua N sau 3 giờ kể từ lúc khởi hành.

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 16 phiếu

Bài tiếp theo

Giải bài 4.4 trang 50 SGK Toán 10 tập 1 – Kết nối tri thức
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập hợp S gồm tất cả các vecto khác 0. Hãy chỉ ra tập hợp S gồm tất cả các vceto khác 0, có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
Giải bài 4.3 trang 50 SGK Toán 10 tập 1 – Kết nối tri thức
Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi BC = AD.
Giải bài 4.2 trang 50 SGK Toán 10 tập 1 – Kết nối tri thức
Trong Hình 4.12, hãy chỉ ra các vecto cùng phương, các cặp vecto ngược hướng và các cặp vecto bằng nhau.
Giải bài 4.1 trang 50 SGK Toán 10 tập 1 – Kết nối tri thức
Cho 3 vectơ a, b, cđều khác 0. Những khẳng định nào sau đây là đúng?
Giải mục 2 trang 47, 48, 49, 50 SGK Toán 10 tập 1 - Kết nối tri thức
Quan sát các làn đường trong Hình 4.5 và cho biết những nhận xét nào sau đây là đúng. Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ Cho hình thang cân ABCD với hai đấy AB, CD, AB < CD. Hãy chỉ ra mỗi quan hệ về đồ dài Trong các điều kiện dưới đây, chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B,
Giải mục 1 trang 47 SGK Toán 10 tập 1 - Kết nối tri thức
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp về hướng nam thì tới đảo B (h.4.2) Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.
Giải câu hỏi mở đầu trang 46 SGK Toán 10 tập 1 – Kết nối tri thức
Nhiệt độ và gió là hai yếu tố luôn cùng được đề cập trong các bản tin dự báo thời tiết. Tuy nhiên, nhiệt độ là đại lượng chỉ có độ lớn, còn gió có cả hướng và độ lớn. Với một đơn vị đo, ta có thể dùng số để biểu diễn nhiệt độ. Đối với các đại lượng gồm hướng và độ lớn như vận tốc gió thì sao? Ta có dùng đối tương toán học nào để biểu diễn chúng?
Lý thuyết Các khái niệm mở đầu
1. KHÁI NIỆM VECTƠ 2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU