Đề thi học kì 2 - Đề số 5
Đề bài

Điền số thích hợp vào ô trống:
\(7\) năm \(8\) tháng \( + \,15\) năm \(6\) tháng \(=\)
năm
tháng.

Một người thợ làm một sản phẩm hết \(2\) giờ \(25\) phút. Hỏi người đó làm \(8\) sản phẩm như thể hết bao nhiêu thời gian?
A. \(16\) giờ \(25\) phút
B. \(17\) giờ \(40\) phút
C. \(18\) giờ \(20\) phút
D. \(19\) giờ \(20\) phút

Điền số thích hợp vào ô trống:
Một đội công nhân chuyển gạo vào \(2\) kho với thời gian chuyển vào kho thứ nhất là \(5\) giờ \(15\) phút.
Thời gian chuyển gạo vào kho thứ hai nhanh gấp \(3\) lần so với kho thứ nhất.
Vậy tổng thời gian chuyển gạo vào cả hai kho là
giờ.
.jpg)
Mai đi từ nhà lúc \(7\) giờ \(15\) phút và đến trường sớm \(8\) phút so với giờ vào học. Lan đi từ nhà lúc \(7\) giờ \(20\) phút và đến trường đúng giờ vào học. Biết giờ vào học là \(8\) giờ. Hỏi Mai và Lan, ai đi từ nhà đến trường mất nhiều thời gian hơn và nhiều hơn bao nhiêu phút?
A. Mai ; \(3\) phút
B. Mai ; \(5\) phút
C. Lan ; \(3\) phút
D. Lan ; \(5\) phút

Điền số thích hợp vào ô trống:
Một người đi bộ rời khỏi nhà lúc \(7\) giờ \(30\) phút và đến chợ lúc \(8\) giờ \(6\) phút, biết quãng đường từ nhà đến chợ dài \(3km\).
Vậy vận tốc của người đó là
km/giờ.

Một con rái cá có thể bơi với vận tốc \(25,2\) km/giờ. Một con ngựa chạy với vận tốc \(5,5\) m/giây. Hỏi trong \(1\) phút, con nào di chuyển được quãng đường dài hơn và dài hơn bao nhiêu mét?
A. Con rái cá; \(9m\)
B. Con rái cá; \(90m\)
C. Con ngựa; \(9m\)
D. Con ngựa; \(90m\)

Quãng đường AB dài \(120km\). Lúc \(7\) giờ \(30\) phút một ô tô đi từ A đến B với vận tốc \(50\) km/giờ và nghỉ trả khách \(45\) phút. Sau đó ô tô đi từ B về A với vận tốc \(60\) km/giờ. Hỏi ô tô về đến A lúc mấy giờ?
A. \(12\) giờ \(39\) phút
B. \(12\) giờ \(19\) phút
C. \(11\) giờ \(54\) phút
D. \(11\) giờ \(9\) phút

Điền số thích hợp vào ô trống:
Một ô tô đi từ thị xã A đến thị xã B với vận tốc là $48$ km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc $54$ km/giờ. Sau \(2\) giờ \(30\) phút hai ô tô gặp nhau.
Vậy quãng đường từ thị xã A đến thị xã B dài
\(km\).

Hai bến sông A và B cách nhau \(40km\). Lúc \(7\) giờ \(20\) phút, một ca nô đi xuôi dòng từ A đến B. Biết vận tốc của ca nô khi đi ngược dòng là \(28\) km/giờ và vận tốc dòng nước là \(2\) km/giờ. Hỏi ca nô đến B lúc mấy giờ?
A. \(8\) giờ \(15\) phút
B. \(8\) giờ \(35\) phút
C. \(8\) giờ \(40\) phút
D. \(8\) giờ \(50\) phút

Một thửa ruộng hình thang có đáy bé bằng \(\dfrac{3}{5}\) đáy lớn, chiều cao bằng $\dfrac{1}{4}$ đáy lớn. Biết đáy lớn hình thang là $260m$. Để làm sạch cỏ trên thửa ruộng, bác Hùng cần $0,75$ giờ cho mỗi $100{m^2}$ đất. Hỏi bác Hùng cần dùng bao nhiêu giờ để làm sạch cỏ trên cả thửa ruộng ấy?
A. \(76,05\) giờ
B. \(101,4\) giờ
C. \(180\) giờ
D. \(202,8\) giờ

Diện tích hình tròn có bán kính \(r = \dfrac{4}{5}m\) là:
A. \(\dfrac{{314}}{{125}}{m^2}\)
B. \(\dfrac{{628}}{{125}}{m^2}\)
C. $\dfrac{{628}}{{625}}{m^2}$
D. \(\dfrac{{1256}}{{625}}{m^2}\)
.jpg)
A. Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
B. Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
C. Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\).
D. Cả A, B, C đều đúng.

Một người thuê thợ sơn mặt trong và mặt ngoài một cái thùng sắt không có nắp dạng hình hộp chữ nhật chiều dài $1,3m$; chiều rộng $0,8m$; chiều cao $1,5m$. Hỏi người ấy phải trả bao nhiêu tiền để sơn cái thùng đó, biết rằng tiền sơn \(1m^2\) là \(35000\) đồng?
A. \(256900\) đồng
B. \(513800\) đồng
C. \(293300\) đồng
D. \(586600\) đồng

Một người làm cái hộp không có nắp bằng bìa cứng dạng hình lập phương có cạnh $14cm$. Tính diện tích bìa cần dùng để làm hộp (không tính mép dán).
A. \(196c{m^2}\)
B. \(784c{m^2}\)
C. \(980c{m^2}\)
D. \(1176c{m^2}\)

Một bể nước dạng hình hộp chữ nhật có chiều dài $2m$ ; chiều rộng $1,2m$ và chiều cao $1,4m$. Hiện tại, lượng nước trong bể chiếm \(\dfrac{2}{5}\) thể tích của bể. Hỏi cần phải đổ thêm vào bể bao nhiêu lít nước để được đầy bể nước?
A. \(134,4\) lít
B. \(201,6\) lít
C. \(1344\) lít
D. \(2016\) lít

Điền số thích hợp vào ô trống:
Cho hình lập phương có cạnh $8dm$ .
Vậy thể tích của hình lập phương đó là
\(d{m^3}\).

Điền số thích hợp vào ô trống:
Một căn phòng hình hộp chữ nhật chứa được \(36\) người và mỗi người có đủ \(4,5{m^3}\) không khí để thở. Biết chiều cao căn phòng là \(4m\).
Vậy diện tích đáy căn phòng đó là
\({m^2}\).

Điền số thích hợp vào ô trống :
Phần nguyên của số thập phân \(24,567\) là

Điền dấu (\(>;\, <;\, =\)) thích hợp vào ô trống :
\(6da{m^2}\,9{m^2}\,\,\)
\(\,\,6,9da{m^2}\)

Điền số thích hợp vào ô trống:
\(4\) tuần lễ có
ngày.

Điền số thích hợp vào ô trống:
Tính bằng cách thuận tiện nhất:
\(14,25 + 5,88 + 35,75 + 16,12\)
\(=\,(14,25 + \)
\() \, +\, (5,88\,+ \)
\()\)
\(=\)
\(+\)
\(=\)

Tính : \(\dfrac{7}{{12}} - \dfrac{1}{4}\).
A. \(\dfrac{1}{2}\)
B. \(\dfrac{1}{3}\)
C. \(\dfrac{2}{3}\)
D. \(\dfrac{3}{4}\)

Một miếng đất hình thang có diện tích là $864{m^2}$, đáy lớn hơn đáy bé 12m. Người ta mở rộng miếng đất bằng cách tăng đáy lớn thêm $5m$ thì được miếng đất hình thang mới có diện tích bằng $924{m^2}$. Tìm độ dài mỗi đáy của miếng đất hình thang lúc chưa mở rộng.
A. Đáy lớn: \(24m\); đáy bé \(12m\)
B. Đáy lớn: \(42m\); đáy bé \(30m\)
C. Đáy lớn: \(78m\); đáy bé \(66m\)
D. Đáy lớn: \(50m\); đáy bé \(38m\)

Cho dãy số như sau:
\(1998\,;\,\,1999\,;\,\,...\,.\)
Số thích hợp điền vào chỗ chấm để có ba số tự nhiên liên tiếp là:
A. \(2000\)
B. \(2001\)
C. \(2002\)
D. \(2003\)

Người ta dùng gạch vuông có cạnh \(20cm\) để ốp xung quanh và đáy của một cái bể hình hộp chữ nhật cao \(1,8m;\) rộng \(2m\) và dài \(35dm\). Tính số viên gạch cần dùng.
A. \(422\) viên gạch
B. \(495\) viên gạch
C. \(670\) viên gạch
D. \(845\) viên gạch

Một ô tô đi từ tỉnh A lúc \(7\) giờ \(40\) phút và đến tỉnh B lúc \(10\) giờ \(4\) phút với vận tốc \(45\)km/giờ. Đến tỉnh B ô tô nghỉ \(45\) phút để lấy hàng rồi quay trở về tỉnh A. Hỏi ô tô trở về A lúc mấy giờ? Biết vận tốc ô tô khi quay về tỉnh A là \(48\)km/giờ.
A. \(\,12\) giờ \(19\) phút
B. \(\,13\) giờ \(4\) phút
C. \(\,13\) giờ \(24\) phút
D. \(\,12\) giờ \(45\) phút

Điền số thích hợp vào ô trống:
Một mảnh đất hình chữ nhật có chu vi \(156m\), chiều dài hơn chiều rộng \(14m\).
Vậy diện tích mảnh đất đó là
\(m^2\).

Một bếp ăn dữ trữ khối lượng gạo đủ cho \(16\) người trong \(15\) ngày. Vì số người thực tế đông hơn dự kiến nên số gạo đó chỉ đủ ăn trong \(12\) ngày. Tính số người đến thêm, biết rằng khẩu phần gạo của mỗi người trong một ngày đều như nhau.
A. \(4\) người
B. \(8\) người
C. \(10\) người
D. \(20\) người

Tìm \(x\), biết: \(x - 3,5 = 12,3:1,25\).
A. \(x = 4,484\)
B. \(x = 6,34\)
C. \(x = 13,34\)
D. \(x = 101,9\)
Lời giải và đáp án

Điền số thích hợp vào ô trống:
\(7\) năm \(8\) tháng \( + \,15\) năm \(6\) tháng \(=\)
năm
tháng.
\(7\) năm \(8\) tháng \( + \,15\) năm \(6\) tháng \(=\)
năm
tháng.
- Đặt tính thẳng hàng và thực hiện tính như đối với phép cộng các số tự nhiên.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
- Nếu số tháng ở kết quả lớn hơn hoặc bằng $12$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn tháng là năm.
Ta đặt tính và thực hiện tính như sau:

Do đó: \(7\) năm \(8\) tháng \( + \,15\) năm \(6\) tháng = \(23\) năm \(2\) tháng.
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(23\,;\,\,2\).
Cần nhớ \(1\) năm \( = 12\) tháng. Học sinh có thể xác định sai \(1\) năm \( = \,10\) tháng nên đổi \(14\) tháng \( = \,1\) năm \(4\) tháng, từ đó tìm ra đáp án sai là \(23\) năm \(4\) tháng.

Một người thợ làm một sản phẩm hết \(2\) giờ \(25\) phút. Hỏi người đó làm \(8\) sản phẩm như thể hết bao nhiêu thời gian?
A. \(16\) giờ \(25\) phút
B. \(17\) giờ \(40\) phút
C. \(18\) giờ \(20\) phút
D. \(19\) giờ \(20\) phút
D. \(19\) giờ \(20\) phút
Tính thời gian người đó làm \(8\) sản phẩm ta lấy thời gian làm một sản phẩm nhân với \(8\).
Người đó làm \(8\) sản phẩm như thể hết số thời gian là:
\(2\) giờ \(25\) phút \( \times \,\,8\,\, = \,\,16\) giờ \(200\) phút \( = \,\,19\) giờ \(20\) phút
Đáp số: \(19\) giờ \(20\) phút.

Điền số thích hợp vào ô trống:
Một đội công nhân chuyển gạo vào \(2\) kho với thời gian chuyển vào kho thứ nhất là \(5\) giờ \(15\) phút.
Thời gian chuyển gạo vào kho thứ hai nhanh gấp \(3\) lần so với kho thứ nhất.
Vậy tổng thời gian chuyển gạo vào cả hai kho là
giờ.
Một đội công nhân chuyển gạo vào \(2\) kho với thời gian chuyển vào kho thứ nhất là \(5\) giờ \(15\) phút.
Thời gian chuyển gạo vào kho thứ hai nhanh gấp \(3\) lần so với kho thứ nhất.
Vậy tổng thời gian chuyển gạo vào cả hai kho là
giờ.
Thời gian chuyển gạo vào kho thứ hai nhanh gấp \(3\) lần thời gian chuyển vào kho thứ nhất nghĩa là để chuyển vào kho thứ hai đội công nhân cần số thời gian ít hơn \(3\) lần thời gian chuyển vào kho thứ nhất.
Để giải bài này ta có thể làm như sau:
- Tìm thời gian chuyển gạo vào kho thứ hai ta lấy thời gian chuyển vào kho thứ nhất chia cho \(3\).
- Tìm thời gian chuyển gạo vào 2 kho ta tìm tổng thời gian chuyển vào kho thứ nhất và thời gian chuyển vào kho thứ hai.
Thời gian chuyển gạo vào kho thứ hai là:
\(5\) giờ \(15\) phút \(:\,3\, = \,1\) giờ $45$ phút
Thời gian chuyển gạo vào cả hai kho là:
\(5\) giờ \(15\) phút \( + \,1\) giờ \(45\) phút \(\, = \,6\) giờ \(60\) phút \(\, = \,7\) giờ
Đáp số: \(\,7\) giờ.
Vậy đáp án đúng điền vào ô trống là \(7\).
Học sinh có thể tính sai thời gian chuyển gạo vào kho thứ hai bằng cách lấy thời gian chuyển vào kho thứ nhất nhân với \(3\).
.jpg)
Mai đi từ nhà lúc \(7\) giờ \(15\) phút và đến trường sớm \(8\) phút so với giờ vào học. Lan đi từ nhà lúc \(7\) giờ \(20\) phút và đến trường đúng giờ vào học. Biết giờ vào học là \(8\) giờ. Hỏi Mai và Lan, ai đi từ nhà đến trường mất nhiều thời gian hơn và nhiều hơn bao nhiêu phút?
A. Mai ; \(3\) phút
B. Mai ; \(5\) phút
C. Lan ; \(3\) phút
D. Lan ; \(5\) phút
C. Lan ; \(3\) phút
- Tìm thời gian lúc Mai đi tới trường: Mai đến trường sớm \(8\) phút tức là đến trường lúc \(8\) giờ kém \(8\) phút hay \(7\) giờ \(52\) phút.
- Tính thời gian Mai đi từ nhà đến trường ta lấy thời gian lúc Mai đi tới trường trừ đi thời gian lúc Mai đi từ nhà.
- Tính thời gian Lan đi từ nhà đến trường ta lấy thời gian lúc Lan đi tới trường trừ đi thời gian lúc Lan đi từ nhà.
- So sánh hai kết quả để tìm ai đi mất nhiều thời gian hơn.
- Tìm thời gian đi nhiều hơn ta lấy số đo thời gian lớn hơn trừ đi số đo thời gian bé hơn.
Mai đến trường sớm \(8\) phút tức là đến trường lúc \(8\) giờ kém \(8\) phút hay \(7\) giờ \(52\) phút.
Thời gian Mai đi từ nhà đến trường là:
\(7\) giờ \(52\) phút \( - \,7\) giờ \(15\) phút \( = \,37\) phút
Thời gian Lan đi từ nhà đến trường là:
\(8\) giờ \( - \,7\) giờ \(20\) phút \( = \,40\) phút
Ta có: \(40\) phút \( > \,37\) phút.
Vây Lan đi từ nhà đến trường mất nhiều thời gian hơn và nhiều hơn số thời gian là:
\(\,\,40\) phút \( - \,37\) phút \( = \,3\) phút
Đáp số: Lan ; \(3\) phút.

Điền số thích hợp vào ô trống:
Một người đi bộ rời khỏi nhà lúc \(7\) giờ \(30\) phút và đến chợ lúc \(8\) giờ \(6\) phút, biết quãng đường từ nhà đến chợ dài \(3km\).
Vậy vận tốc của người đó là
km/giờ.
Một người đi bộ rời khỏi nhà lúc \(7\) giờ \(30\) phút và đến chợ lúc \(8\) giờ \(6\) phút, biết quãng đường từ nhà đến chợ dài \(3km\).
Vậy vận tốc của người đó là
km/giờ.
- Tìm thời gian đi từ nhà đến chợ \( = \,\,8\) giờ \(6\) phút \( - \,\,7\) giờ \(30\) phút.
- Đổi số đo thời gian dưới dạng số tự nhiên sang số thập phân.
- Tìm vận tốc của ô tô bằng cách lấy quãng đường chia cho thời gian.
Thời gian người đó đi từ nhà đến chợ là:
\(8\) giờ \(6\) phút \( - \,\,7\) giờ \(30\) phút \( = \,36\) phút
Đổi: \(36\) phút $ = {\rm{ }}0,6$ giờ
Vận tốc của người đó là:
$3:0,6 = 5$ (km/giờ)
Đáp số: \(5\) km/giờ.

Một con rái cá có thể bơi với vận tốc \(25,2\) km/giờ. Một con ngựa chạy với vận tốc \(5,5\) m/giây. Hỏi trong \(1\) phút, con nào di chuyển được quãng đường dài hơn và dài hơn bao nhiêu mét?
A. Con rái cá; \(9m\)
B. Con rái cá; \(90m\)
C. Con ngựa; \(9m\)
D. Con ngựa; \(90m\)
B. Con rái cá; \(90m\)
- Đổi \(1\) phút \( = \,\dfrac{1}{{60}}\) giờ, tính độ dài quãng đường con rái cá bơi được theo đơn vị là ki-lô-mét bằng cách lấy vận tốc nhân với thời gian.
- Đổi kết quả vừa tìm được sang đơn vị là mét.
- Đổi \(1\) phút \( = 60\) giây, tính độ dài quãng đường con ngựa chạy được theo đơn vị là mét bằng cách lấy vận tốc nhân với thời gian.
- So sánh kết quả để tìm con nào di chuyển được quãng đường dài hơn.
- Tính quãng đường dài hơn bao nhiêu ki-lô-mét ta lấy quãng đường dài hơn trừ quãng đường ngắn hơn.
Đổi: \(1\) phút \( = \dfrac{1}{{60}}\) giờ; \(1\) phút \( = 60\) giây.
Quãng đường con rái cá bơi được trong \(1\) phút là:
\(25,2 \times \dfrac{1}{{60}} = 0,42\;(km)\)
Đổi: \(0,42km = 420m\)
Quãng đường con ngựa chạy được trong \(1\) phút là:
\(5,5 \times 60 = 330\;(m)\)
Ta có: \(420m > 330m\)
Vậy trong \(1\) phút con rái cá di chuyển được quãng đường dài hơn và dài hơn số mét là:
\(420m - 330m = 90\;(m)\)
Đáp số: Con rái cá; \(90m\).
Có nhiều cách để tìm quãng đường con rái cá bơi được, ví dụ như đổi vận tốc bơi của rái cá sang đơn vị là m/giây hoặc m/phút, hay km/phút.
Ví dụ cụ thể, vận tốc bơi của rái cá là \(25,2\) km/giờ nghĩa là trong \(1\) giờ con rái cá bơi được \(25,2km\).
Mà \(25,2km = 25200m\), \(1\) giờ \( = 60\) phút nên trong \(1\) phút con rái cá bơi được số mét là:
\(25200:60 = 420(m)\), tức là vận tốc của rái cá là \(420\) m/phút.
Cách đổi các đơn vị khác ta làm tương tự.
Học sinh chọn cách phù hợp để giải bài.

Quãng đường AB dài \(120km\). Lúc \(7\) giờ \(30\) phút một ô tô đi từ A đến B với vận tốc \(50\) km/giờ và nghỉ trả khách \(45\) phút. Sau đó ô tô đi từ B về A với vận tốc \(60\) km/giờ. Hỏi ô tô về đến A lúc mấy giờ?
A. \(12\) giờ \(39\) phút
B. \(12\) giờ \(19\) phút
C. \(11\) giờ \(54\) phút
D. \(11\) giờ \(9\) phút
A. \(12\) giờ \(39\) phút
- Tính thời gian ô tô đi từ A đến B ta lấy quãng đường chia cho vận tốc khi ô tô đi từ A đến B.
- Tính thời gian ô tô đi từ B về A ta lấy quãng đường chia cho vận tốc khi ô tô đi từ B về A.
- Tính tổng thời gian ô tô đi từ A đến B và từ B về A (kể cả thời gian nghỉ).
- Tính thời gian lúc ô tô về đến A ta tìm tổng thời gian lúc ô tô khởi hành đi từ A và tổng thời gian ô tô đi từ A đến B và từ B về A (kể cả thời gian nghỉ).
Thời gian ô tô đi từ A đến B là:
\(120:50 = 2,4\) (giờ)
Đổi \(2,4\) giờ \( = 2\) giờ \(24\) phút
Thời gian ô tô đi từ B về A:
\(120:60 = 2\) (giờ)
Thời gian ô tô đi từ A đến B và từ B về A (kể cả thời gian nghỉ) là:
\(2\) giờ \(24\) phút \( + \,2\) giờ \( + \,45\) phút \( = \,4\) giờ \(69\) phút
Đổi \(\,4\) giờ \(69\) phút \( = \,5\) giờ \(9\) phút
Ô tô về đến A lúc:
\(7\) giờ \(30\) phút \( + \,5\) giờ \(9\) phút \( = \,12\) giờ \(39\) phút
Đáp số: \(12\) giờ \(39\) phút.
Có thể tìm thời gian lúc ô tô bắt đầu từ B đi về A bằng cách lấy thời gian lúc ô tô khởi hành từ A cộng thời gian đi từ A đến B rồi cộng với thời gian nghỉ trả khách, sau đó tìm thời gian lúc ô tô về đến A bằng cách lấy thời gian lúc ô tô khởi hành từ B cộng thời gian đi từ B về A.

Điền số thích hợp vào ô trống:
Một ô tô đi từ thị xã A đến thị xã B với vận tốc là $48$ km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc $54$ km/giờ. Sau \(2\) giờ \(30\) phút hai ô tô gặp nhau.
Vậy quãng đường từ thị xã A đến thị xã B dài
\(km\).
Một ô tô đi từ thị xã A đến thị xã B với vận tốc là $48$ km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc $54$ km/giờ. Sau \(2\) giờ \(30\) phút hai ô tô gặp nhau.
Vậy quãng đường từ thị xã A đến thị xã B dài
\(km\).
Theo đề bài, hai ô tô xuất phát cùng lúc. Để giải bài này ta làm như sau:
- Đổi số đo thời gian sang dạng số thập phân có đơn vị là giờ.
- Tính tổng vận tốc hai ô tô.
- Tính quãng đường ta lấy tổng hai vận tốc nhân với thời gian đi để gặp nhau.
Đổi: \(2\) giờ \(30\) phút \( = \,\,2,5\) giờ
Tổng vận tốc hai ô tô là:
\(48 + 54 = 102\) (km/giờ)
Quãng đường từ thị xã A đến thị xã B dài số ki-lô-mét là:
\(102 \times 2,5 = 255 \;(km)\)
Đáp số: \(255km\).
Vậy đáp án đúng điền vào ô trống là \(255\).

Hai bến sông A và B cách nhau \(40km\). Lúc \(7\) giờ \(20\) phút, một ca nô đi xuôi dòng từ A đến B. Biết vận tốc của ca nô khi đi ngược dòng là \(28\) km/giờ và vận tốc dòng nước là \(2\) km/giờ. Hỏi ca nô đến B lúc mấy giờ?
A. \(8\) giờ \(15\) phút
B. \(8\) giờ \(35\) phút
C. \(8\) giờ \(40\) phút
D. \(8\) giờ \(50\) phút
B. \(8\) giờ \(35\) phút
- Tính vận tốc của ca nô khi nước yên lặng và vận tốc xuôi dòng theo công thức:
Vận tốc khi nước lặng \(=\) vận tốc ngược dòng \(+\) vận tốc dòng nước;
Vận tốc xuôi dòng \(=\) vận tốc khi nước lặng \(+\) vận tốc dòng nước
- Tính thời gian đi xuôi dòng ta lấy độ dài từ bến A đến bến B chia cho vận tốc đi xuôi dòng.
- Tính thời gian ca nô đến B theo công thức:
Thời gian đến \(=\) thời gian xuất phát \(+\) thời gian đi \(+\) thời gian nghỉ (nếu có).
Vận tốc của ca nô khi nước lặng là:
\(28 + 2 = 30\) (km/giờ)
Vận tốc của ca nô khi đi xuôi dòng là:
\(30 + 2 = 32\) (km/giờ)
Ca nô đi xuôi dòng từ A đến B hết số thời gian là:
\(40:32 = 1,25\) (giờ)
Đổi \(1,25\) giờ \( = \,1\) giờ \(15\) phút
Ca nô đến B lúc:
\(7\) giờ \(20\) phút \( + \,1\) giờ \(15\) phút \( = \,8\) giờ \(35\) phút
Đáp số: \(8\) giờ \(35\) phút.

Một thửa ruộng hình thang có đáy bé bằng \(\dfrac{3}{5}\) đáy lớn, chiều cao bằng $\dfrac{1}{4}$ đáy lớn. Biết đáy lớn hình thang là $260m$. Để làm sạch cỏ trên thửa ruộng, bác Hùng cần $0,75$ giờ cho mỗi $100{m^2}$ đất. Hỏi bác Hùng cần dùng bao nhiêu giờ để làm sạch cỏ trên cả thửa ruộng ấy?
A. \(76,05\) giờ
B. \(101,4\) giờ
C. \(180\) giờ
D. \(202,8\) giờ
B. \(101,4\) giờ
- Tìm đáy lớn và chiều cao theo quy tắc: muốn tìm phân số của một số ta lấy số đó nhân với phân số.
- Tìm diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
- Tìm số giờ để làm sạch cỏ theo bài toán tỉ lệ thuận: tìm tỉ số giữa diện tích và \(100m^2\), diện tích gấp \(100m^2\) bao nhiêu lần thì số giờ để làm sạch cỏ cũng gấp \(0,75\) giờ bấy nhiêu lần.
Độ dài đáy bé của thửa ruộng đó là:
$260 \times \dfrac{3}{5} = 156\;(m)$
Chiều cao của thửa ruộng đó là:
$260 \times \dfrac{1}{4} = 65\;(m)$
Diện tích của thửa ruộng đó là:
$\dfrac{{(156 + 260) \times 65}}{2} = 13520\;({m^2})$
$13520{m^2}$ gấp $100{m^2}$ số lần là:
$13520:100 = 135,2$ (lần)
Bác Hùng cần dùng số giờ để làm sạch cỏ trên cả thửa ruộng đó là:
\(0,75 \times 135,2 = 101,4\) (giờ)
Đáp số: \(101,4\) giờ.
- Học sinh cần nhớ cách tìm phân số của một số.
- Bước cuối tìm số giờ cần để làm sạch cỏ ta có thể làm gộp thành một bước: \(13520:100 \times 0,75\)

Diện tích hình tròn có bán kính \(r = \dfrac{4}{5}m\) là:
A. \(\dfrac{{314}}{{125}}{m^2}\)
B. \(\dfrac{{628}}{{125}}{m^2}\)
C. $\dfrac{{628}}{{625}}{m^2}$
D. \(\dfrac{{1256}}{{625}}{m^2}\)
D. \(\dfrac{{1256}}{{625}}{m^2}\)
Áp dụng công thức: \(S = r \times r \times 3,14\), trong đó \(r\) là bán kính hình tròn.
Diện tích hình tròn đó là:
\(\frac{4}{5} \times \frac{4}{5} \times 3,14 = \frac{4}{5} \times \frac{4}{5} \times \frac{{314}}{{100}}\)
\(= \frac{{4 \times 4 \times 314}}{{5 \times 5 \times 100}} = \frac{{1256}}{{625}}\) \(\left( {{m^2}} \right)\)
.jpg)
A. Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
B. Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
C. Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\).
D. Cả A, B, C đều đúng.
D. Cả A, B, C đều đúng.
Dựa vào quy tắc tính diện tích các hình tam giác, hình thang, hình tròn.
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
- Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
- Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\).
Vậy cả A, B, C đều đúng.

Một người thuê thợ sơn mặt trong và mặt ngoài một cái thùng sắt không có nắp dạng hình hộp chữ nhật chiều dài $1,3m$; chiều rộng $0,8m$; chiều cao $1,5m$. Hỏi người ấy phải trả bao nhiêu tiền để sơn cái thùng đó, biết rằng tiền sơn \(1m^2\) là \(35000\) đồng?
A. \(256900\) đồng
B. \(513800\) đồng
C. \(293300\) đồng
D. \(586600\) đồng
B. \(513800\) đồng
Vì người đó muốn sơn cả mặt trong và mặt ngoài của thùng sắt không nắp nên diện tích cần sơn bằng hai lần tổng diện tích xung quanh và diện tích một mặt đáy.
Để giải bài này ta có thể làm như sau:
- Tính diện tích xung quanh của thùng sắt ta lấy chu vi đáy nhân với chiều cao.
- Tính diện tích đáy của thùng sắt ta lấy chiều dài nhân với chiều rộng.
- Tính diện tích cần sơn khi sơn mặt trong và mặt ngoài cái thùng đó ta lấy tổng diện tích xung quanh của thùng và diện tích đáy rồi nhân với \(2\).
- Tính số tiền để sơn cái thùng đó ta lấy số tiền khi sơn \(1{m^2}\) nhân với diện tích cần sơn.
Diện tích xung quanh của thùng sắt đó là:
\((1,3 + 0,8) \times 2 \times 1,5 = 6,3 \; ({m^2})\)
Diện tích đáy của thùng sắt đó là:
\(1,3 \times 0,8 = 1,04\;({m^2})\)
Diện tích cần sơn là:
\((6,3 + 1,04) \times 2 = 14,68\;({m^2})\)
Số tiền người đó phải trả để sơn cái thùng đó là:
\(35000 \times 14,68 = 513800\) (đồng)
Đáp số: \(513800\) đồng.
- Một số học sinh không đọc kĩ đề nên tính diện tích cần sơn thùng chính bằng diện tích toàn phần của hình hộp chữ nhật.
- Học sinh có thể chỉ tính diện tích khi sơn một mặt trong hoặc mặt ngoài thùng, tức là tính tổng diện tích xung quanh và diện tích một mặt đáy.

Một người làm cái hộp không có nắp bằng bìa cứng dạng hình lập phương có cạnh $14cm$. Tính diện tích bìa cần dùng để làm hộp (không tính mép dán).
A. \(196c{m^2}\)
B. \(784c{m^2}\)
C. \(980c{m^2}\)
D. \(1176c{m^2}\)
C. \(980c{m^2}\)
Vì cái hộp đó có dạng là hình lập phương và không có nắp nên cái hộp đó có \(5\) mặt. Do đó diện tích bìa cần dùng để làm hộp gấp \(5\) lần diện tích một mặt.
Để giải bài này ta có thể thực hiện các bước như sau:
- Tính diện tích một mặt của cái hộp ta lấy độ dài một cạnh nhân với chính nó.
- Tính diện tích bìa cần dùng để làm cái hộp đó ta lấy diện tích một mặt của cái hộp đó nhân với \(5\).
Diện tích một mặt của cái hộp đó là:
\(14 \times 14 = 196 \;(c{m^2})\)
Diện tích bìa cần dùng để làm cái hộp đó là:
\(196 \times 5 = 980 \; (c{m^2})\)
Đáp số: \(980c{m^2}\).
Học sinh có thể xác định sai diện tích bìa cần dùng khi xác định thùng đó có \(4\) mặt (tính diện tích xung quanh) hoặc xác định thùng đó có \(6\) mặt (tính diện tích toàn phần).

Một bể nước dạng hình hộp chữ nhật có chiều dài $2m$ ; chiều rộng $1,2m$ và chiều cao $1,4m$. Hiện tại, lượng nước trong bể chiếm \(\dfrac{2}{5}\) thể tích của bể. Hỏi cần phải đổ thêm vào bể bao nhiêu lít nước để được đầy bể nước?
A. \(134,4\) lít
B. \(201,6\) lít
C. \(1344\) lít
D. \(2016\) lít
D. \(2016\) lít
Thể tích nước khi bể đầy nước chính là thể thể tích của hình hộp chữ nhật có chiều dài $2m$ ; chiều rộng $1,2m$ và chiều cao $1,4m$.
Để giải bài ta có thể làm như sau:
- Tính thể tích bể nước đó theo công thức: Thể tích = Chiều dài × chiều rộng × chiều cao.
- Tính thể tích nước đang có trong bể ta lấy thể tích bể nước nhân với \(\dfrac{2}{5}\).
- Tính thể tích cần đổ thêm vào bể ta lấy thể tích bể nước trừ đi thể tích nước đang có trong bể.
- Đổi thể tích từ đơn vị mét khối sang đơn vị đề-xi-mét khối rồi tính số lít nước.
Thể tích của bể nước là:
\(2 \times 1,2 \times 1,4 = 3,36 \; ({m^3})\)
Thể tích nước đang có trong bể là:
\(3,36 \times \dfrac{2}{5} = 1,344\;({m^3})\)
Thể tích cần đổ thêm vào bể để bể đầy nước là:
\(3,36 - 1,344 = 2,016 \;({m^3})\)
Đổi \(2,016{m^3} = 2016d{m^3} = 2016\) lít
Đáp số: \(2016\) lít.
- Có thể tìm thể tích nước với đơn vị đề-xi-mét khối (hay lít) từ đầu sau đó tìm lượng nước cần đổ thêm với đơn vị lít.
- Học sinh có thể làm sai khi tính thể tích nước cần đổ thêm chính bằng \(\dfrac{2}{5}\) thể tích bể nước.

Điền số thích hợp vào ô trống:
Cho hình lập phương có cạnh $8dm$ .
Vậy thể tích của hình lập phương đó là
\(d{m^3}\).
Cho hình lập phương có cạnh $8dm$ .
Vậy thể tích của hình lập phương đó là
\(d{m^3}\).
Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh.
Thể tích hình lập phương đó là:
\(8 \times 8 \times 8 = 512\;(d{m^3})\)
Đáp số: \(512d{m^3}\).
Vậy đáp án đúng điền vào ô trống là \(512\).

Điền số thích hợp vào ô trống:
Một căn phòng hình hộp chữ nhật chứa được \(36\) người và mỗi người có đủ \(4,5{m^3}\) không khí để thở. Biết chiều cao căn phòng là \(4m\).
Vậy diện tích đáy căn phòng đó là
\({m^2}\).
Một căn phòng hình hộp chữ nhật chứa được \(36\) người và mỗi người có đủ \(4,5{m^3}\) không khí để thở. Biết chiều cao căn phòng là \(4m\).
Vậy diện tích đáy căn phòng đó là
\({m^2}\).
Thể tích không khí chứa trong phòng chính bằng thể tích của căn phòng đó.
Để giải bài này ta có thể làm như sau:
- Tìm thể tích không khí ta lấy số mét khối không khí để thở của một người nhân với số người.
Từ đó tìm được thể tích căn phòng.
- Tìm diện tích đáy của căn phòng ta lấy thể tích chia cho chiều cao.
Thể tích không khí chứa trong phòng là:
\(4,5 \times 36 = 162 \;({m^3})\)
Diện tích đáy căn phòng đó là:
\(162:4 = 40,5 \;({m^2})\)
Đáp số: \(40,5{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(40,5\).

Điền số thích hợp vào ô trống :
Phần nguyên của số thập phân \(24,567\) là
Phần nguyên của số thập phân \(24,567\) là
Dựa vào hàng và cấu tạo của số thập phân : các chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân.
Phần nguyên của số thập phân \(24,567\) là \(24\).
Vậy đáp án đúng điền vào ô trống là \(24\).
Học sinh có thể nhầm lẫn chọn phần thập phân là \(567\) điền vào ô trống; hoặc chỉ điền \(2\) hoặc \(4\) vào ô trống.

Điền dấu (\(>;\, <;\, =\)) thích hợp vào ô trống :
\(6da{m^2}\,9{m^2}\,\,\)
\(\,\,6,9da{m^2}\)
\(6da{m^2}\,9{m^2}\,\,\)
\(\,\,6,9da{m^2}\)
- Đưa hai số đo về cùng một dạng là dạng số thập phân.
- Xác định các số đo đã cùng đơn vị đo chưa, nếu không cùng đơn vị đo ta phải đổi thành cùng 1 đơn vị đo.
- Xác định các phần nguyên và phần thập phân để so sánh bình thường như so sánh các số thập phân.
Hai số đã cho chưa cùng đơn vị đo, ta sẽ đưa về cùng dạng số thập phân có đơn vị đo là \(d{am^2}\).
Ta có \(6da{m^2}\,\,9{m^2} = 6\dfrac{9}{{100}}da{m^2} = 6,09da{m^2}\).
Mà \(6,09da{m^2} < 6,9da{m^2}\).
Vậy \(6da{m^2}\,9{m^2}\, < \,6,9da{m^2}\).

Điền số thích hợp vào ô trống:
\(4\) tuần lễ có
ngày.
\(4\) tuần lễ có
ngày.
Dựa vào bảng đơn vị đo thời gian: \(1\) tuần lễ có \(7\) ngày.
\(1\) tuần lễ có \(7\) ngày nên \(4\) tuần lễ có \(28\) ngày.
Vậy đáp án đúng điền vào ô trống là \(28\).

Điền số thích hợp vào ô trống:
Tính bằng cách thuận tiện nhất:
\(14,25 + 5,88 + 35,75 + 16,12\)
\(=\,(14,25 + \)
\() \, +\, (5,88\,+ \)
\()\)
\(=\)
\(+\)
\(=\)
Tính bằng cách thuận tiện nhất:
\(14,25 + 5,88 + 35,75 + 16,12\)
\(=\,(14,25 + \)
\() \, +\, (5,88\,+ \)
\()\)
\(=\)
\(+\)
\(=\)
Áp dụng tính chất giao hoán và kết hợp của phép cộng các số thập phân để nhóm các số thập phân có phần thập phân cộng với nhau thành các số tròn chục, tròn trăm, tròn nghìn, ...
Áp dụng tính chất giao hoán và kết hợp của phép cộng các số thập phân ta có:
\(\begin{array}{l}14,25 + 5,88 + 35,75 + 16,12\\ = (14,25 + 35,75) + (5,88 + 16,12)\\ = 50 + 22\\ = 72\end{array}\)
Vậy các số cần điền vào lần lượt từ trái sang phải, từ trên xuống dưới là \(35,75\,\,;\,\,\,16,12\,\,;\,\,\,50\,\,;\,\,\,22\,\,;\,\,\,72\).

Tính : \(\dfrac{7}{{12}} - \dfrac{1}{4}\).
A. \(\dfrac{1}{2}\)
B. \(\dfrac{1}{3}\)
C. \(\dfrac{2}{3}\)
D. \(\dfrac{3}{4}\)
B. \(\dfrac{1}{3}\)
Quy đồng mẫu số hai phân số đó rồi trừ hai phân số đã quy đồng. Nếu phân số thu được chưa tối giản thì ta rút gọn thành phân số tối giản.
Ta có: \(\dfrac{7}{{12}} - \dfrac{1}{4} = \dfrac{7}{{12}} - \dfrac{3}{{12}} = \dfrac{4}{{12}} = \dfrac{1}{3}\)
Vậy \(\dfrac{7}{{12}} - \dfrac{1}{4} = \dfrac{1}{3}\)
- Học sinh có thể làm sai khi tính hiệu hai phân số bằng cách lấy tử số trừ cho tử số, mẫu số trừ cho mẫu số rồi rút gọn và chọn đáp án sai là D.

Một miếng đất hình thang có diện tích là $864{m^2}$, đáy lớn hơn đáy bé 12m. Người ta mở rộng miếng đất bằng cách tăng đáy lớn thêm $5m$ thì được miếng đất hình thang mới có diện tích bằng $924{m^2}$. Tìm độ dài mỗi đáy của miếng đất hình thang lúc chưa mở rộng.
A. Đáy lớn: \(24m\); đáy bé \(12m\)
B. Đáy lớn: \(42m\); đáy bé \(30m\)
C. Đáy lớn: \(78m\); đáy bé \(66m\)
D. Đáy lớn: \(50m\); đáy bé \(38m\)
B. Đáy lớn: \(42m\); đáy bé \(30m\)
- Tính diện tích phần đất tăng thêm.
Diện tích phần đất tăng thêm chính là diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là chiều cao của hình thang.
- Tính chiều cao của hình thang ta lấy diện tích phần đất tăng thêm nhân với \(2\) rồi chia cho độ dài đáy \(5m\).
- Tính tổng độ dài hai đáy của hình thang ta lấy diện tích hình thang nhân với \(2\) rồi chia cho chiều cao.
- Giải bài toán tìm hai số khi biết tổng và hiệu để tìm độ dài mỗi đáy theo công thức:
Số lớn = (tổng + hiệu) \(:\,\,2\) ; Số bé = (tổng – hiệu) \(:\,\,2\)
Ta có hình vẽ như sau:
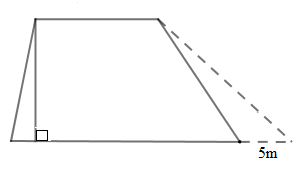
Sau khi mở rộng, diện tích miếng đất tăng thêm là:
$924 - 864 = 60\;({m^2})$
Diện tích phần đất tăng thêm chính là diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là chiều cao của hình thang.
Chiều cao của miếng đất hình thang là:
\(60 \times 2:5 = 24\;(m)\)
Tổng độ dài hai đáy của hình thang là:
\(864 \times 2:24 = 72\;(m)\)
Độ dài đáy lớn của miếng đất đó là:
\((72 + 12):2 = 42\;(m)\)
Độ dài đáy bé của miếng đất đó là:
\(72 - 42 = 30\;(m)\)
Đáp số: đáy lớn: \(42m\); đáy bé: \(30m\).
- Học sinh có thể làm sai khi tính chiều cao bằng cách lấy diện tích phần đất tăng thêm chia cho \(5\).
- Học sinh có thể làm sai khi tính tổng độ dài hai đáy bằng cách lấy diện tích hình thang chia cho chiều cao.

Cho dãy số như sau:
\(1998\,;\,\,1999\,;\,\,...\,.\)
Số thích hợp điền vào chỗ chấm để có ba số tự nhiên liên tiếp là:
A. \(2000\)
B. \(2001\)
C. \(2002\)
D. \(2003\)
A. \(2000\)
- Hai số tự nhiên liên tiếp hơn kém nhau \(1\) đơn vị.
- Số đứng sau lớn hơn số đứng trước.
Số liền sau của số \(1999\) là số \(2000\).
Vậy số thích hợp điền vào chỗ chấm để có ba số tự nhiên liên tiếp là \(2000\).

Người ta dùng gạch vuông có cạnh \(20cm\) để ốp xung quanh và đáy của một cái bể hình hộp chữ nhật cao \(1,8m;\) rộng \(2m\) và dài \(35dm\). Tính số viên gạch cần dùng.
A. \(422\) viên gạch
B. \(495\) viên gạch
C. \(670\) viên gạch
D. \(845\) viên gạch
C. \(670\) viên gạch
Diện tích cần ốp gạch chính là diện tích xung quanh và diện tích một mặt đáy của cái bể.
Để giải ta có thể thực hiện các bước như sau:
- Đổi chiều dài sang đơn vị mét để ba kích thước cùng đơn vị đo.
- Tính diện tích xung quanh của cái bể ta lấy chu vi đáy nhân với chiều cao.
- Tính diện tích đáy ta lấy chiều dài nhân với chiều rộng.
- Tính diện tích cần ốp gạch ta lấy diện tích xung quanh cộng với diện tích một đáy.
- Tính diện tích một viên gạch ta lấy cạnh nhân với cạnh rồi đổi sang đơn vị diện tích là mét vuông.
- Tính số viên gạch cần dùng ta lấy diện tích cần ốp gạch chia cho diện tích một viên gạch.
Đổi \(35dm = 3,5m\)
Diện tích xung quanh của cái bể là:
\((3,5 + 2) \times 2 \times 1,8 = 19,8\;({m^2})\)
Diện tích đáy của cái bể là:
\(3,5 \times 2 = 7\;({m^2})\)
Diện tích cần ốp gạch là:
\(19,8 + 7 = 26,8\;({m^2})\)
Diện tích một viên gạch là:
\(20 \times 20 = 400\;(c{m^2})\)
Đổi \(400c{m^2} = 0,04{m^2}\)
Số viên gạch cần dùng là:
\(26,8:0,04 = 670\) (viên gạch)
Đáp số: \(670\) viên gạch.
- Học sinh có thể làm sai khi tính diện tích xung quanh bằng \((3,5 + 2) \times 1,8 = 9,9({m^2})\), từ đó chọn đáp án sai là A.
- Học sinh có thể xác định sai diện tích cần ốp gạch bằng diện tích xung quanh, từ đó chọn đáp án sai là B.
- Học sinh có thể xác định sai diện tích cần ốp gạch bằng diện tích xung quanh cộng với diện tích hai đáy, từ đó chọn đáp án sai là D.

Một ô tô đi từ tỉnh A lúc \(7\) giờ \(40\) phút và đến tỉnh B lúc \(10\) giờ \(4\) phút với vận tốc \(45\)km/giờ. Đến tỉnh B ô tô nghỉ \(45\) phút để lấy hàng rồi quay trở về tỉnh A. Hỏi ô tô trở về A lúc mấy giờ? Biết vận tốc ô tô khi quay về tỉnh A là \(48\)km/giờ.
A. \(\,12\) giờ \(19\) phút
B. \(\,13\) giờ \(4\) phút
C. \(\,13\) giờ \(24\) phút
D. \(\,12\) giờ \(45\) phút
B. \(\,13\) giờ \(4\) phút
- Tính thời gian ô tô đi từ A đến B \(=\) thời gian lúc ô tô đến B \(-\) thời gian lúc ô tô đi từ A.
- Đổi số đo thời gian vừa tìm được sang dạng số thập phân có đơn vị là giờ.
- Tính độ dài quãng đường AB ta lấy vận tốc nhân với thời gian.
- Tính thời gian lúc ô tô bắt đầu từ B về A \(=\) thời gian lúc ô tô đến B \(+\) thời gian ô tô nghỉ để lấy hàng.
- Tính thời gian ô tô đi từ B về A ta lấy quãng đường chia cho vận tốc.
- Đổi số đo thời gian vừa tìm được sang dạng số tự nhiên.
- Tính thời gian lúc ô tô về đến A \(=\) thời gian lúc ô tô từ B bắt đầu từ B về \(+\) thời gian ô tô đi từ B về A.
Ô tô đi từ A đến B hết số thời gian là:
\(10\) giờ \(4\) phút \( - \,7\) giờ \(40\) phút \( = \,2\) giờ \(24\) phút
Đổi \(\,2\) giờ \(24\) phút \( = \,2,4\) giờ
Quãng đường AB dài là:
\(45 \times 2,4 = 108\;(km)\)
Ô tô bắt đầu đi từ B về A lúc:
\(10\) giờ \(4\) phút \( + \,45\) phút \( = \,10\) giờ \(49\) phút
Ô tô đi từ B về A hết số thời gian là:
\(108:48 = 2,25\) (giờ)
Đổi \(2,25\) giờ \( = \,2\) giờ \(15\) phút
Ô tô về đến A lúc:
\(\,10\) giờ \(49\) phút \( + \,2\) giờ \(15\) phút \( = \,12\) giờ \(64\) phút
Đổi \(\,12\) giờ \(64\) phút \( = \,13\) giờ \(4\) phút
Đáp số: \(\,13\) giờ \(4\) phút.
- Có thể tính “gộp”:
Tính thời gian lúc ô tô về đến A \(=\) thời gian lúc ô tô đến B \(+\) thời gian ô tô nghỉ để lấy hàng \(+\) thời gian ô tô đi từ B về A.
- Học sinh có thể tính sai thời gian khi ô tô trở về A khi không cộng thêm thời gian ô tô nghỉ để lấy hàng.

Điền số thích hợp vào ô trống:
Một mảnh đất hình chữ nhật có chu vi \(156m\), chiều dài hơn chiều rộng \(14m\).
Vậy diện tích mảnh đất đó là
\(m^2\).
Một mảnh đất hình chữ nhật có chu vi \(156m\), chiều dài hơn chiều rộng \(14m\).
Vậy diện tích mảnh đất đó là
\(m^2\).
- Tìm nửa chu vi hình chữ nhật ta lấy chu vi chia cho \(2\).
- Từ đó ta có tổng và hiệu của hai số. Đây là dạng toán tìm hai số khi biết tổng và hiệu của hai số đó. Để tìm hai số ta áp dụng công thức sau:
Số lớn \( = \) (tổng \( + \)hiệu ) \(:\,2\) ; Số bé \( = \) (tổng \( - \)hiệu ) \(:\,2\)
- Tìm diện tích mảnh đất ta lấy chiều dài nhân với chiều rộng.
Nửa chu vi mảnh đất đó là:
\(156:2 = 78\;(m)\)
Chiều dài mảnh đất đó là:
\((78 + 14):2 = 46\;(m)\)
Chiều rộng mảnh đất đó là:
\(78 - 46 = 32\;(m)\)
Diện tích mảnh đất đó là:
\(46 \times 32 = 1472\;({m^2})\)
Đáp số: \(1472{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(1472\).
Học sinh có thể làm sai khi xác định tổng của chiều dài và chiều rộng là \(156m\), từ đó áp dụng công thức tìm được chiều dài là \(85m\) và chiều rộng \(71m\).

Một bếp ăn dữ trữ khối lượng gạo đủ cho \(16\) người trong \(15\) ngày. Vì số người thực tế đông hơn dự kiến nên số gạo đó chỉ đủ ăn trong \(12\) ngày. Tính số người đến thêm, biết rằng khẩu phần gạo của mỗi người trong một ngày đều như nhau.
A. \(4\) người
B. \(8\) người
C. \(10\) người
D. \(20\) người
A. \(4\) người
Với cùng một lượng gạo đã dự trữ, càng có nhiều người ăn thì số ngày để ăn hết gạo sẽ giảm đi. Vậy đây là bài toán tỉ lệ nghịch.
Đối với dạng toán về quan hệ tỉ lệ, ta có thể làm theo 2 cách sau:
Cách 1: Dùng phương pháp rút về đơn vị.
Cách 2: Dùng phương pháp tìm tỉ số.
Tóm tắt:
\(15\) ngày: \(16\) người :
\(12\) ngày : …người
Số người đến thêm: … người?
Cách giải: (phương pháp rút về đơn vị)
\(1\) người ăn hết số gạo đó trong số ngày là:
\(15 \times 16 = 240\) (ngày)
Để ăn hết số gạo đó trong \(12\) ngày thì cần số người là:
\(240:12 = 20\) (người)
Số người đến thêm là :
\(20 - 16 = 4\) (người)
Đáp số: \(4\) người.
Học sinh có thể làm sai khi tính số người đến thêm chính là số người thực tế đã ăn số gạo đó nên chọn đáp án sai là D.

Tìm \(x\), biết: \(x - 3,5 = 12,3:1,25\).
A. \(x = 4,484\)
B. \(x = 6,34\)
C. \(x = 13,34\)
D. \(x = 101,9\)
C. \(x = 13,34\)
- Tính kết quả của vế phải trước.
- \(x\) ở vị trí số bị trừ, để tìm \(x\) ta lấy hiệu cộng với số trừ.
Ta có:
\(\begin{array}{l}x - 3,5 = 12,3:1,25\\x - 3,5 = 9,84\\x = 9,84 + 3,5\\x = 13,34\end{array}\)
Vậy \( x=13,34\).
- Học sinh có thể tính sai kết quả vế phải bằng \(0,984\) hoặc \(98,4\), từ đó chọn đáp án sai là A hoặc D.
- Học sinh có thể làm sai khi tính \(x = 9,84 - 3,5\) nên chọn đáp án sai là B.
>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 5 trên Tuyensinh247.com. Cam kết giúp con lớp 5 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |










Danh sách bình luận