Đề thi học kì 2 - Đề số 4
Đề bài

\(\dfrac{5}{4}\) ngày \(= \,….\) giờ.
Số thích hợp điền vào chỗ chấm là:
A. \(54\) giờ
B. \(50\) giờ
C. \(30\) giờ
D. \(25\) giờ

Viết số thập phân thích hợp vào ô trống :
\(204\) giây =
phút.

Điền dấu (\(>;\, <;\, = \)) thích hợp vào ô trống:
$16$ giờ \(15\) phút \( - \,\,3\) giờ $45$ phút
$9$ giờ $25$ phút $ + {\rm{ 2}}$ giờ \(39\) phút

Tính: \(12\) phút \(25\) giây \( \times \,3\, + \,\)\(27\) phút \(32\) giây \( \times \,4\)
A. \(4\) giờ \(19\) phút \(8\) giây
B.\(3\) giờ \(54\) phút \(15\) giây
C. \(2\) giờ \(18\) phút \(32\) giây
D. \(2\) giờ \(27\) phút \(23\) giây

Điền số thích hợp vào ô trống:
Bác thợ mộc làm một bộ bàn ghế gồm \(1\) cái bàn và \(4\) cái ghế hết \(22\) giờ \(30\) phút.
Biết rằng thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế.
Vậy trung bình làm một cái ghế mất
giờ
phút.

Muốn tính vận tốc ta lấy quãng đường chia cho thời gian. Đúng hay sai?
A. Đúng
B. Sai

Điền số thích hợp vào ô trống:
Quãng đường AB gồm đoạn lên dốc dài \(16,2km\) và đoạn xuống dốc dài \(16,8km\).
Một ô tô đi lên dốc hết \(54\) phút và đi xuống dốc hết \(42\) phút.
Vậy vận tốc lên dốc là
km/giờ; vận tốc xuống dốc là
km/giờ;
vận tốc trung bình của ô tô trên cả quãng đường AB là
km/giờ.

Điền số thích hợp vào ô trống:
Trên quãng đường dài $54km$, người đi xe máy đi với vận tốc \(36\) km/giờ.
Vậy người đó đi hết quãng đường trong
giờ.

Điền số thích hợp vào ô trống:
Một ô tô đi từ thị xã A đến thị xã B với vận tốc là $48$ km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc $54$ km/giờ. Sau \(2\) giờ \(30\) phút hai ô tô gặp nhau.
Vậy quãng đường từ thị xã A đến thị xã B dài
\(km\).
Cho hình vẽ như bên dưới:
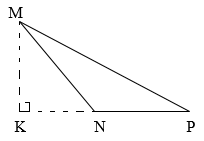
Trong tam giác \(MNP\), \(MK\) là chiều cao tương ứng với:
A. Cạnh \(MN\)
B. Cạnh \(NP\)
C. Cạnh \(MP\)
D. Cạnh \(KN\)

Điền số thích hợp vào ô trống:
Trung bình cộng hai đáy hình thang là $17,5m$. Biết đáy lớn hơn đáy bé $13m$. Chiều cao bằng \(\dfrac{3}{4}\) đáy lớn.
Vậy diện tích hình thang đó là
\({m^2}.\)
Điền số thích hợp vào ô trống:
Cho hình vẽ như bên dưới:
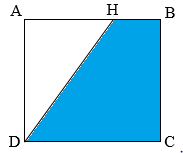
Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\).
Vậy diện tích hình thang \(HBCD\) là
\(d{m^2}\).
Tính diện tích bông hoa được tô màu trong hình vẽ sau, biết hình vuông \(ABCD\) có độ dài cạnh là \(6cm\).
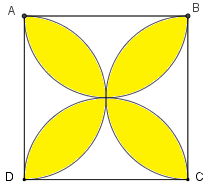
A. \(5,13c{m^2}\)
B. \(7,065c{m^2}\)
C. \(20,52c{m^2}\)
D. \(28,26c{m^2}\)

Một người thuê thợ sơn mặt trong và mặt ngoài một cái thùng sắt không có nắp dạng hình hộp chữ nhật chiều dài $1,3m$; chiều rộng $0,8m$; chiều cao $1,5m$. Hỏi người ấy phải trả bao nhiêu tiền để sơn cái thùng đó, biết rằng tiền sơn \(1m^2\) là \(35000\) đồng?
A. \(256900\) đồng
B. \(513800\) đồng
C. \(293300\) đồng
D. \(586600\) đồng
Điền số thích hợp vào ô trống:
Cho hình lập phương như hình vẽ:
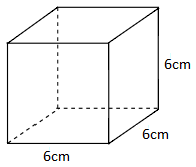
Diện tích xung quanh của hình lập phương đó là
\(c{m^2}\).

Bác Bình cần làm \(2\) cái thùng hình lập phương bằng sắt không có nắp cạnh $1,8m$ . Hỏi Bác sơn cả bên trong và bên ngoài \(2\) cái thùng đó thì phải mua bao nhiêu ki-lô-gam sơn, biết rằng cứ $20{m^2}$ thì cần $5kg$ sơn.
A. \(32,4kg\)
B. \(16,2kg\)
C. \(8,1kg\)
D. \(4,05kg\)

Một bể nước hình hộp chữ nhật có các kích thước trong lòng bể là chiều dài $3m$ ; chiều rộng kém chiều dài \(1,8m\); chiều cao $1,5m$. Hỏi bể đó chứa được nhiều nhất bao nhiêu lít nước? (\(1\) lít \( = 1d{m^3}\))
A. \(5,4\) lít
B. \(81\) lít
C. \(5400\) lít
D. \(8100\) lít
Điền số thích hợp vào ô trống:
Cho tam giác ABC có số đo như hình vẽ:
Diện tích tam giác ABC là
\(d{m^2}\).

Một bể nước dạng hình hộp chữ nhật có các kích thước đo ở trong lòng bể là: chiều dài là $1,5m$; chiều rộng $1,2m$, chiều cao \(2m\). Mặt nước cách miệng bể \(0,5m\). Người ta mở khóa cho nước chảy ra khỏi bể, sau \(5\) giờ thì bể cạn. Hỏi nước chảy ra khỏi bể mỗi phút được bao nhiêu lít?
A. \(3\) lít
B. \(6\) lít
C. \(9\) lít
D. \(12\) lít

Phân số \(\dfrac{5}{{100}}\) được viết dưới dạng số thập phân là:
A. \(0,5\)
B. \(0,05\)
C. \(0,005\)
D. \(0,0005\)

Trong bảng đơn vị đo diện tích, đơn vị lớn gấp bao nhiêu lần đơn vị bé tiếp liền?
A. \(10\) lần
B. \(100\) lần
C. \(1000\) lần
D. \(10000\) lần

Điền dấu (\(>;\, <;\, =\)) thích hợp vào ô trống:
\(15{m^3}\;27d{m^3}\,\,\)
\(\,\,15,027{m^3}\)

Điền số thích hợp vào ô trống:
\(667724 + 69058=\)

Điền số thích hợp vào ô trống:
Cho hình vẽ như sau:
Biết hình chữ nhật $ABCD$ có diện tích bằng \(96c{m^2};{\rm{ }}MC{\rm{ }} = {\rm{ }}MD;\,\,BN = \dfrac{2}{3}BC\) (như hình vẽ).
Diện tích tam giác $AMN$ là
\(cm^2\).

Điền số thích hợp vào ô trống:
Một bể nước dạng hình hộp chữ nhật có kích thước ở trong lòng bể là: chiều dài \(2,5m\), chiều rộng \(1,5m\) và chiều cao \(1,8m\). Khi bể không có nước người ta mở vòi cho nước chảy vào bể, mỗi giờ được \(750\) lít nước.
Vậy bể sẽ đầy nước sau
giờ.

Điền số thích hợp vào ô trống:
\(45\) phút \(15\) giây \( - \,17\) phút \(28\) giây \( = \)
phút
giây.

Một ô tô đi từ tỉnh A lúc \(7\) giờ \(40\) phút và đến tỉnh B lúc \(10\) giờ \(4\) phút với vận tốc \(45\)km/giờ. Đến tỉnh B ô tô nghỉ \(45\) phút để lấy hàng rồi quay trở về tỉnh A. Hỏi ô tô trở về A lúc mấy giờ? Biết vận tốc ô tô khi quay về tỉnh A là \(48\)km/giờ.
A. \(\,12\) giờ \(19\) phút
B. \(\,13\) giờ \(4\) phút
C. \(\,13\) giờ \(24\) phút
D. \(\,12\) giờ \(45\) phút

Điền số thích hợp vào ô trống:
Một cửa hàng bán đường trong ba ngày, trung bình mỗi ngày cửa hàng bán được \(4\) tạ đường. Ngày đầu cửa hàng bán được \(468kg\) đường, ngày thứ hai cửa hàng bán được \(75\% \) số đường bán được trong ngày đầu.
Vậy ngày thứ ba cửa hàng bán được
ki-lô-gam đường.

Điền số thích hợp vào ô trống:
Một ô tô du lịch khởi hành từ A lúc \(5\) giờ \(40\) phút để đi về B. Cùng lúc đó một ô tô chở hàng đi từ B về A. Hai ô tô gặp nhau lúc \(8\) giờ \(30\) phút. Quãng đường AB dài \(306km\) và vận tốc ô tô du lịch bằng \(\dfrac{4}{5}\) vận tốc ô tô chở hàng.
Vậy vận tốc của ô tô du lịch là
km/giờ, vận tốc của ô tô chở hàng là
km/giờ.

Tính giá trị biểu thức: \(50 - 22,5:12,5 + 36,5:10\).
A. \(3,87\)
B. \(5,85\)
C. \(51,67\)
D. \(51,85\)
Lời giải và đáp án

\(\dfrac{5}{4}\) ngày \(= \,….\) giờ.
Số thích hợp điền vào chỗ chấm là:
A. \(54\) giờ
B. \(50\) giờ
C. \(30\) giờ
D. \(25\) giờ
C. \(30\) giờ
\(1\) ngày $=\,24$ giờ . Muốn đổi một số từ đơn vị ngày sang giờ ta lấy \(24\) giờ nhân với số đó.
Ta có \(1\) ngày $=\, 24$ giờ.
Do đó, \(\dfrac{5}{4}\) ngày $ = 24$ giờ \( \times \,\dfrac{5}{4}\,=\,30\) giờ.
Vậy \(\dfrac{5}{4}\) ngày \(=\,30\) giờ.
Học sinh có thể làm sai khi xác định \(1\) ngày = $20$ giờ.

Viết số thập phân thích hợp vào ô trống :
\(204\) giây =
phút.
\(204\) giây =
phút.
\(1\) phút $ = 60$ giây. Khi đổi một số có đơn vị là giây sang phút ta chỉ cần lấy số đó chia cho $60$.
Ta có:
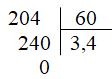
\(204\) giây \(=\, 3,4\) phút.
Vậy số thập phân thích hợp điền vào ô trống là \(3,4\).

Điền dấu (\(>;\, <;\, = \)) thích hợp vào ô trống:
$16$ giờ \(15\) phút \( - \,\,3\) giờ $45$ phút
$9$ giờ $25$ phút $ + {\rm{ 2}}$ giờ \(39\) phút
$16$ giờ \(15\) phút \( - \,\,3\) giờ $45$ phút
$9$ giờ $25$ phút $ + {\rm{ 2}}$ giờ \(39\) phút
- Tính kết quả của từng vế.
- So sánh các kết quả đó với nhau.
Ta có:
+) $16$ giờ \(15\) phút \( - \, 3\) giờ $45$ phút \( = \,15\) giờ \(75\) phút \( - \,3\) giờ $45$ phút \( = \,12\) giờ $30$ phút.
+) $9$ giờ $25$ phút $ + \,{\rm{ 2}}$ giờ \(39\) phút \( = \,11\) giờ \(64\) phút \( = \,12\) giờ \(4\) phút (vì \(64\) phút \( = \,1\) giờ \(4\) phút)
Mà \(\,12\) giờ $30$ phút \( > \,12\) giờ $4$ phút.
Nên $16$ giờ \(15\) phút \( - \,3\) giờ $45$ phút $ > \,\,9$ giờ $25$ phút $ +\; {\rm{ 2}}$ giờ \(39\) phút.

Tính: \(12\) phút \(25\) giây \( \times \,3\, + \,\)\(27\) phút \(32\) giây \( \times \,4\)
A. \(4\) giờ \(19\) phút \(8\) giây
B.\(3\) giờ \(54\) phút \(15\) giây
C. \(2\) giờ \(18\) phút \(32\) giây
D. \(2\) giờ \(27\) phút \(23\) giây
D. \(2\) giờ \(27\) phút \(23\) giây
- Ta thực hiện tính giá trị biểu thức như đối với các số tự nhiên, tính lần lượt phép nhân trước, phép cộng sau.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
- Nếu số phút lớn hơn hoặc bằng \(60\) thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của phút là giờ; số giây lớn hơn hoặc bằng \(60\) thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của giây là phút.
Ta có:
\(12\) phút \(25\) giây \( \times \,\,\,3\,\,\, + \,\,27\) phút \(32\) giây \( \times \,\,4\)
\( = \,\,36\) phút \(75\) giây \( + \,\,108\) phút \(128\) giây
\( = \,\,37\) phút \(15\) giây \( + \,\,110\) phút \(8\) giây
\( = \,\,147\) phút \(23\) giây
\( = \,\,2\) giờ \(27\) phút \(23\) giây
- Cần chú ý tính toán cẩn thận.
- Học sinh có thể làm sai khi tính giá trị phép tính \(12\) phút \(25\) giây \( \times \,\,\,3\), được kết quả đem cộng với \(\,27\) phút \(32\) giây, sau đó mới nhân với \(4\), từ đó chọn đáp án sai là A.

Điền số thích hợp vào ô trống:
Bác thợ mộc làm một bộ bàn ghế gồm \(1\) cái bàn và \(4\) cái ghế hết \(22\) giờ \(30\) phút.
Biết rằng thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế.
Vậy trung bình làm một cái ghế mất
giờ
phút.
Bác thợ mộc làm một bộ bàn ghế gồm \(1\) cái bàn và \(4\) cái ghế hết \(22\) giờ \(30\) phút.
Biết rằng thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế.
Vậy trung bình làm một cái ghế mất
giờ
phút.
Theo đề bài thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế nên thời gian làm \(4\) cái ghế gấp \(2\) lần thời gian làm \(1\) cái bàn.
Lại có thời gian làm \(1\) cái bàn và \(4\) cái ghế hết \(22\) giờ \(30\) phút.
Từ đó ta có bài toán dạng tìm hai số khi biết tổng và tỉ số. Ta vẽ sơ đồ biểu thị thời gian làm \(1\) cái bàn gồm \(1\) phần và thời gian làm \(4\) cái ghế gồm \(2\) phần như thế. Coi thời gian làm \(1\) cái bàn là số bé, thời gian làm \(4\) cái ghế là số lớn, ta tìm hai số theo công thức:
Số bé = Giá trị một phần × số phần của số bé
hoặc
Số lớn = Giá trị một phần × số phần của số lớn.
Theo đề bài thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế nên thời gian làm \(4\) cái ghế gấp \(2\) lần thời gian làm \(1\) cái bàn.
Ta có sơ đồ:
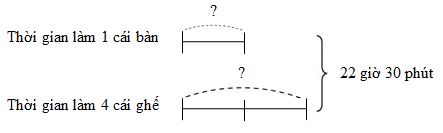
Theo sơ đồ, tổng số phần bằng nhau là:
\(1 + 2 = 3\) (phần)
Giá trị một phần hay thời gian làm \(1\) cái bàn là:
\(22\) giờ \(30\) phút \(:\,3\, = \,7\) giờ \(30\) phút
Thời gian trung bình để làm \(1\) cái ghế là:
\(\,7\) giờ \(30\) phút \(:\,2\, = \,3\) giờ \(45\) phút
Đáp số: \(3\) giờ \(45\) phút.
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(3\,;\,\,45\).
- Chú ý đọc kĩ đề bài và tính toán cẩn thận.
- Cần nhớ phương pháp giải của dạng toán tìm hai số khi biết tổng và tỉ số.
- Học sinh có thể giải theo cách khác, ví dụ vì thời gian làm \(1\) cái bàn bằng thời gian làm \(2\) cái ghế nên có thể coi thời gian làm \(1\) cái bàn và \(4\) cái ghế bằng thời gian làm \(2\) cái ghế và \(4\) cái ghế, tức là thời gian làm \(6\) cái ghế là \(22\) giờ \(30\) phút, từ đó tìm được thời gian làm \(1\) cái ghế.

Muốn tính vận tốc ta lấy quãng đường chia cho thời gian. Đúng hay sai?
A. Đúng
B. Sai
A. Đúng
B. Sai
Muốn tính vận tốc ta lấy quãng đường chia cho thời gian.
Phát biểu trên là đúng.

Điền số thích hợp vào ô trống:
Quãng đường AB gồm đoạn lên dốc dài \(16,2km\) và đoạn xuống dốc dài \(16,8km\).
Một ô tô đi lên dốc hết \(54\) phút và đi xuống dốc hết \(42\) phút.
Vậy vận tốc lên dốc là
km/giờ; vận tốc xuống dốc là
km/giờ;
vận tốc trung bình của ô tô trên cả quãng đường AB là
km/giờ.
Quãng đường AB gồm đoạn lên dốc dài \(16,2km\) và đoạn xuống dốc dài \(16,8km\).
Một ô tô đi lên dốc hết \(54\) phút và đi xuống dốc hết \(42\) phút.
Vậy vận tốc lên dốc là
km/giờ; vận tốc xuống dốc là
km/giờ;
vận tốc trung bình của ô tô trên cả quãng đường AB là
km/giờ.
- Đổi \(54\) phút và \(42\) phút sang đơn vị là giờ: muốn đổi một số từ đơn vị phút sang đơn vị giờ ta lấy số đó chia cho \(60\).
- Tính vận tốc lên dốc ta lấy quãng đường đi lên dốc chia cho thời gian đi lên dốc.
- Tính vận tốc xuống dốc ta lấy quãng đường đi xuống dốc chia cho thời gian đi xuống dốc.
- Tính vận tốc trung bình của ô tô trên cả quãng đường AB ta lấy độ dài quãng đường AB chia cho tổng thời gian đi hết quãng đường AB, hay lấy tổng độ dài đoạn lên dốc và đoạn xuống dốc chia cho tổng thời gian lên dốc và xuống dốc.
Đổi: \(54\) phút \( = 0,9\) giờ ; \(42\) phút \( = 0,7\) giờ
Vận tốc lên dốc của ô tô là:
\(16,2:0,9 = 18\) (km/giờ)
Vận tốc xuống dốc của ô tô là:
\(16,8:0,7 = 24\) (km/giờ)
Vận tốc trung bình của ô tô trên cả quãng đường AB là:
\((16,2 + 16,8):(0,9 + 0,7) = 20,625\) (km/giờ)
Đáp số: Vận tốc lên dốc: \(18\) km/giờ; vận tốc xuống dốc: \(24\) km/giờ;
Vận tốc trung bình: \(20,625\) km/giờ.
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trên xuống dưới, từ trái sang phải là \(18\,;\,\,24\,;\,\,20,625\).
- Học sinh chú ý tính toán cẩn thận. Học sinh có thể làm sai khi đổi \(54\) phút và \(42\) phút sang đơn vị là giờ.
- Nhiều học sinh tính sai vận tốc trung bình trên đoạn đường AB bằng cách tìm trung bình cộng vận tốc lên dốc và vận tốc xuống dốc.

Điền số thích hợp vào ô trống:
Trên quãng đường dài $54km$, người đi xe máy đi với vận tốc \(36\) km/giờ.
Vậy người đó đi hết quãng đường trong
giờ.
Trên quãng đường dài $54km$, người đi xe máy đi với vận tốc \(36\) km/giờ.
Vậy người đó đi hết quãng đường trong
giờ.
Đơn vị của quãng đường và vận tốc đã tương ứng với nhau nên để tính thời gian ta lấy quãng đường chia cho vận tốc.
Thời gian để người đi xe máy đi hết quãng đường đó là:
\(54:36 = 1,5\) (giờ)
Đáp số: \(1,5\) giờ.
Vậy đáp án đúng điền vào ô trống là \(1,5\).

Điền số thích hợp vào ô trống:
Một ô tô đi từ thị xã A đến thị xã B với vận tốc là $48$ km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc $54$ km/giờ. Sau \(2\) giờ \(30\) phút hai ô tô gặp nhau.
Vậy quãng đường từ thị xã A đến thị xã B dài
\(km\).
Một ô tô đi từ thị xã A đến thị xã B với vận tốc là $48$ km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc $54$ km/giờ. Sau \(2\) giờ \(30\) phút hai ô tô gặp nhau.
Vậy quãng đường từ thị xã A đến thị xã B dài
\(km\).
Theo đề bài, hai ô tô xuất phát cùng lúc. Để giải bài này ta làm như sau:
- Đổi số đo thời gian sang dạng số thập phân có đơn vị là giờ.
- Tính tổng vận tốc hai ô tô.
- Tính quãng đường ta lấy tổng hai vận tốc nhân với thời gian đi để gặp nhau.
Đổi: \(2\) giờ \(30\) phút \( = \,\,2,5\) giờ
Tổng vận tốc hai ô tô là:
\(48 + 54 = 102\) (km/giờ)
Quãng đường từ thị xã A đến thị xã B dài số ki-lô-mét là:
\(102 \times 2,5 = 255 \;(km)\)
Đáp số: \(255km\).
Vậy đáp án đúng điền vào ô trống là \(255\).
Cho hình vẽ như bên dưới:

Trong tam giác \(MNP\), \(MK\) là chiều cao tương ứng với:
A. Cạnh \(MN\)
B. Cạnh \(NP\)
C. Cạnh \(MP\)
D. Cạnh \(KN\)
B. Cạnh \(NP\)
Trong hình tam giác, độ dài đoạn thẳng từ đỉnh vuông góc với đáy tương ứng gọi là chiều cao của hình tam giác.
Hình tam giác \(MNP\) có \(MK\) vuông góc với \(NP \), do đó \(MK\) là chiều cao tương ứng với cạnh đáy \(NP\).

Điền số thích hợp vào ô trống:
Trung bình cộng hai đáy hình thang là $17,5m$. Biết đáy lớn hơn đáy bé $13m$. Chiều cao bằng \(\dfrac{3}{4}\) đáy lớn.
Vậy diện tích hình thang đó là
\({m^2}.\)
Trung bình cộng hai đáy hình thang là $17,5m$. Biết đáy lớn hơn đáy bé $13m$. Chiều cao bằng \(\dfrac{3}{4}\) đáy lớn.
Vậy diện tích hình thang đó là
\({m^2}.\)
Muốn tính được diện tích hình thang ta phải biết độ dài hai đáy và chiều cao. Ta có thể giải bài này như sau:
- Tính tổng độ dài hai đáy ta lấy trung bình cộng nhân với \(2\). Khi đó ta có bài toán tìm hai số khi biết tổng và hiệu của hai số. Ta tìm độ dài hai đáy theo công thức:
Số lớn = (tổng + hiệu) \(:2\) ; Số bé = (tổng – hiệu) \(:2\)
- Tìm chiều cao ta lấy đáy lớn nhân với \(\dfrac{3}{4}\).
- Tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
Tổng độ dài hai đáy của hình thang là:
$17,5 \times 2 = 35\;(m)$
Độ dài đáy lớn của hình thang là:
$(35 + 13):2 = 24\;(m)$
Độ dài đáy bé của hình thang là:
$35 - 24 = 11\;(m)$
Chiều cao của hình thang là:
$24 \times \dfrac{3}{4} = 18\;(m)$
Diện tích của hình thang là:
$(24 + 11) \times 18:2 = 315\;({m^2})$
Đáp số: \(315{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(315\).
Học sinh cần nhớ công thức tính tổng khi biết trung bình cộng và cách tìm hai số khi biết tổng và hiệu của hai số đó.
Điền số thích hợp vào ô trống:
Cho hình vẽ như bên dưới:

Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\).
Vậy diện tích hình thang \(HBCD\) là
\(d{m^2}\).
Cho hình vẽ như bên dưới:

Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\).
Vậy diện tích hình thang \(HBCD\) là
\(d{m^2}\).
- Tìm độ dài cạnh hình vuông.
- Tìm độ dài các cạnh đáy và chiều cao của hình thang sau đó để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho \(2\).
Ta có \(50 \times 50 = 2500\). Vậy độ dài cạnh hình vuông \(ABCD\) là \(50dm\) hay \(AB = BC = CD = AD = 50dm\).
Ta có \(HBCD\) là hình thang vuông với chiều cao là cạnh \(BC\), hai đáy là \(HB,\,\,DC\).
Độ dài cạnh \(AH\) là:
\(50:100 \times 70 = 35\;(dm)\)
Độ dài cạnh \(HB\) là:
\(50 - 35 = 15\;(dm)\)
Diện tích hình thang \(HBCD\) là:
\((15 + 50) \times 50:2 = 1625\;(d{m^2})\)
Đáp số: \(1625d{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(1625\).
Có thể tính hình thang \(HBCD\) bằng cách lấy diện tích hình vuông \(ABCD\) trừ đi diện tích diện tích tam giác \(ADH\).
Tính diện tích bông hoa được tô màu trong hình vẽ sau, biết hình vuông \(ABCD\) có độ dài cạnh là \(6cm\).

A. \(5,13c{m^2}\)
B. \(7,065c{m^2}\)
C. \(20,52c{m^2}\)
D. \(28,26c{m^2}\)
C. \(20,52c{m^2}\)
- Gọi \(H,R,S,T\) lần lượt là trung điểm của các cạnh \(AB,BC,CD,DA\) và \(O\) là giao điểm của hai cạnh \(HS\) và \(RT\). Ta chia hình vuông ban đầu thành \(4\) hình vuông bằng nhau có cạnh là \(3cm\) (xem hình vẽ ở bài giải).
- Tính diện tích hình vuông \(AHOT\).
- Diện tích phần \({S_1}\) bằng diện tích hình vuông \(AHOT\) trừ đi \(\dfrac{1}{4}\) diện tích hình tròn tâm \(T\) bán kính \(3cm\).
- Diện tích phần \({S_2}\) bằng diện tích phần \({S_1}\).
- Diện tích một cánh hoa bằng diện tích hình vuông \(AHOT\) trừ đi tổng diện tích hai phần \({S_1}\) và \({S_2}\).
- Diện tích bông hoa được tô màu bằng diện tích một cánh hoa nhân với \(4\) (do \(4\) cánh hoa có diện tích bằng nhau).
Gọi \(H,R,S,T\) lần lượt là trung điểm của các cạnh \(AB,BC,CD,DA\) và \(O\) là giao điểm của hai cạnh \(HS\) và \(RT\). Ta chia hình vuông ban đầu thành \(4\) hình vuông bằng nhau như hình vẽ.
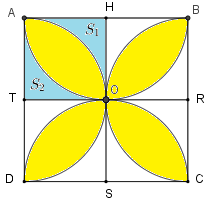
Độ dài cạnh của mỗi hình vuông nhỏ là:
\(6:2 = 3\;(cm)\)
Nhận xét rằng diện tích \(4\) hình vuông nhỏ đều bằng nhau, \(2\) phần không được tô màu ở mỗi hình vuông nhỏ đều bằng nhau và diện tích mỗi cánh hoa đều bằng nhau.
Diện tích hình vuông \(AHOT\) là:
\(3 \times 3 = 9\;(c{m^2})\)
Diện tích hình tròn tâm \(T\) bán kính \(3cm\) là:
\(3 \times 3 \times 3,14 = 28,26\;(c{m^2})\)
\(\dfrac{1}{4}\) diện tích của hình tròn tâm \(T\) bán kính \(3cm\) là:
\(28,26 \times \dfrac{1}{4} = 7,065\;(c{m^2})\)
Diện tích phần \({S_1}\) là:
\(9 - 7,065 = 1,935\;(c{m^2})\)
Ta có phần \({S_1}\) và phần \({S_2}\) có diện tích bằng nhau và bằng \(1,935c{m^2}\).
Diện tích \(1\) cánh hoa là:
\(9 - (1,935 + 1,935) = 5,13\;(c{m^2})\)
Diện tích bông hoa được tô màu là:
\(5,13 \times 4 = 20,52\;(c{m^2})\)
Đáp số: \(20,52c{m^2}\).
Có thể tính diện tích bông hoa được tô màu bằng cách lấy diện tích hình vuông \(ABCD\) trừ đi diện tích phần không được tô màu (màu trắng), tức là lấy diện tích hình vuông \(ABCD\) trừ đi \(8\) lần diện tích phần \({S_1}\).

Một người thuê thợ sơn mặt trong và mặt ngoài một cái thùng sắt không có nắp dạng hình hộp chữ nhật chiều dài $1,3m$; chiều rộng $0,8m$; chiều cao $1,5m$. Hỏi người ấy phải trả bao nhiêu tiền để sơn cái thùng đó, biết rằng tiền sơn \(1m^2\) là \(35000\) đồng?
A. \(256900\) đồng
B. \(513800\) đồng
C. \(293300\) đồng
D. \(586600\) đồng
B. \(513800\) đồng
Vì người đó muốn sơn cả mặt trong và mặt ngoài của thùng sắt không nắp nên diện tích cần sơn bằng hai lần tổng diện tích xung quanh và diện tích một mặt đáy.
Để giải bài này ta có thể làm như sau:
- Tính diện tích xung quanh của thùng sắt ta lấy chu vi đáy nhân với chiều cao.
- Tính diện tích đáy của thùng sắt ta lấy chiều dài nhân với chiều rộng.
- Tính diện tích cần sơn khi sơn mặt trong và mặt ngoài cái thùng đó ta lấy tổng diện tích xung quanh của thùng và diện tích đáy rồi nhân với \(2\).
- Tính số tiền để sơn cái thùng đó ta lấy số tiền khi sơn \(1{m^2}\) nhân với diện tích cần sơn.
Diện tích xung quanh của thùng sắt đó là:
\((1,3 + 0,8) \times 2 \times 1,5 = 6,3 \; ({m^2})\)
Diện tích đáy của thùng sắt đó là:
\(1,3 \times 0,8 = 1,04\;({m^2})\)
Diện tích cần sơn là:
\((6,3 + 1,04) \times 2 = 14,68\;({m^2})\)
Số tiền người đó phải trả để sơn cái thùng đó là:
\(35000 \times 14,68 = 513800\) (đồng)
Đáp số: \(513800\) đồng.
- Một số học sinh không đọc kĩ đề nên tính diện tích cần sơn thùng chính bằng diện tích toàn phần của hình hộp chữ nhật.
- Học sinh có thể chỉ tính diện tích khi sơn một mặt trong hoặc mặt ngoài thùng, tức là tính tổng diện tích xung quanh và diện tích một mặt đáy.
Điền số thích hợp vào ô trống:
Cho hình lập phương như hình vẽ:

Diện tích xung quanh của hình lập phương đó là
\(c{m^2}\).
Cho hình lập phương như hình vẽ:

Diện tích xung quanh của hình lập phương đó là
\(c{m^2}\).
- Tính diện tích một mặt của hình lập phương ta lấy độ dài một cạnh nhân với chính nó.
- Tính diện tích xung quanh của hình lập phương ta lấy diện tích một mặt nhân với \(4\).
Diện tích một mặt của hình lập phương đó là:
\(6 \times 6 = 36\;(c{m^2})\)
Diện tích xung quanh của hình lập phương đó là:
\(36 \times 4 = 144\;(c{m^2})\)
Đáp số: \(144c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(144\).
Tính diện tích xung quanh ta có thể giải “gộp” là \((6 \times 6) \times 4 = 144(c{m^2})\).

Bác Bình cần làm \(2\) cái thùng hình lập phương bằng sắt không có nắp cạnh $1,8m$ . Hỏi Bác sơn cả bên trong và bên ngoài \(2\) cái thùng đó thì phải mua bao nhiêu ki-lô-gam sơn, biết rằng cứ $20{m^2}$ thì cần $5kg$ sơn.
A. \(32,4kg\)
B. \(16,2kg\)
C. \(8,1kg\)
D. \(4,05kg\)
B. \(16,2kg\)
Vì cái thùng đó có dạng là hình lập phương và không có nắp nên cái hộp đó có \(5\) mặt. Diện tích khi sơn bên trong (hoặc bên ngoài) của \(1\) thùng bằng diện tích một mặt nhân với \(5\).
Để giải ta có thể thực hiện các bước như sau:
- Tính diện tích một mặt của cái thùng ta lấy độ dài một cạnh nhân với chính nó.
- Tính diện tích cần sơn khi sơn bên trong của \(1\) cái thùng ta lấy diện tích một mặt nhân với \(5\).
- Tính diện tích cần sơn khi sơn bên trong và bên ngoài của \(1\) cái thùng ta lấy diện tích cần sơn khi sơn bên trong nhân với \(2\).
- Tính khối lượng cần sơn \(1\) cái thùng ta lấy diện tích cần sơn chia cho \(20\) rồi nhân với \(4\) (dạng toán tỉ lệ thuận).
- Tính khối lượng cần sơn \(2\) cái thùng ta lấy khối lượng cần sơn \(1\) cái thùng nhân với \(2\)
nhân với \(2\).
Diện tích một mặt của cái thùng đó là:
$1,8 \times 1,8 = 3,24\;({m^2})$
Diện tích cần sơn khi sơn bên trong của \(1\) cái thùng:
$3,24 \times 5 = 16,2\; ({m^2})$
Diện tích cần sơn khi sơn bên trong và bên ngoài của \(1\) cái thùng là:
$16,2 \times 2 = 32,4\; ({m^2})$
Khối lượng sơn ta cần dùng để sơn \(1\) cái thùng là:
\(32,4:20 \times 5 = 8,1\;(kg)\)
Khối lượng sơn ta cần dùng để sơn \(2\) cái thùng là:
\(8,1 \times 2 = 16,2\;(kg)\)
Đáp số: \(16,2kg\).
- Ta có thể tính diện tích cần sơn khi sơn bên trong và bên ngoài của \(2\) cái thùng sau đó tìm khối lượng sơn cần mua.
- Học sinh có thể làm sai khi tính diện tích cần sơn của $1$ thùng (chỉ tính sơn một bên) từ đó tìm khối lượng sơn sẽ sai.

Một bể nước hình hộp chữ nhật có các kích thước trong lòng bể là chiều dài $3m$ ; chiều rộng kém chiều dài \(1,8m\); chiều cao $1,5m$. Hỏi bể đó chứa được nhiều nhất bao nhiêu lít nước? (\(1\) lít \( = 1d{m^3}\))
A. \(5,4\) lít
B. \(81\) lít
C. \(5400\) lít
D. \(8100\) lít
C. \(5400\) lít
Số lít nước bể có thể chứa được nhiều nhất bằng với thể tích của bể (tính theo đơn vị đề-xi-mét khối).
Để giải bài này ta có thể làm như sau:
- Tính chiều rộng của bể nước ta lấy chiều dài trừ đi \(1,8m\).
- Tính thể tích của bể nước đó theo công thức: Thể tích = Chiều dài × chiều rộng × chiều cao.
- Đổi thể tích từ đơn vị mét khối sang đơn vị đề-xi-mét khối rồi tính số lít nước.
Chiều rộng của bể nước đó là:
\(3 - 1,8 = 1,2 \;(m)\)
Thể tích của bể nước đó là:
\(3 \times 1,2 \times 1,5 = 5,4 \; ({m^3})\)
\(5,4{m^3} = 5400d{m^3} = 5400\) lít
Số lít nước bể có thể chứa được nhiều nhất bằng với thể tích của bể và bằng \(5400\) lít.
Đáp số: \(5400\) lít.
- Học sinh có thể không đọc kĩ đề bài và tính chiều rộng là \(1,8m\) sau đó tính thể tích ra \(8,1{m^3}\). Học sinh có thể chọn đáp án sai là \(8,1\) lít hoặc \(8100\) lít.
- Học sinh có thể tính đúng thể tích là \(5,4{m^3}\) nhưng chưa đổi ra đơn vị \(d{m^3}\) mà đưa ra kết quả sai là \(5,4\) lít.
Điền số thích hợp vào ô trống:
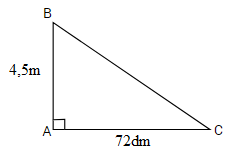
Cho tam giác ABC có số đo như hình vẽ:

Diện tích tam giác ABC là
\(d{m^2}\).
Cho tam giác ABC có số đo như hình vẽ:

Diện tích tam giác ABC là
\(d{m^2}\).
- Đổi độ dài hai cạnh góc vuông về cùng một đơn vị đo là đề-xi-mét.
- Tính diện tích tam giác vuông ta tìm tích độ dài hai cạnh góc vuông rồi chia cho \(2\).
Đổi \(4,5m = 45dm\)
Diện tích tam giác \(ABC\) là:
\(45 \times 72:2 = 1620 \; (d{m^2})\)
Đáp số: \(1620d{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(1620\).
Học sinh cần nhớ quy tắc tính diện tích tam giác vuông. Một số học sinh có thể chỉ tìm tích hai cạnh góc vuông và không chia cho \(2\).

Một bể nước dạng hình hộp chữ nhật có các kích thước đo ở trong lòng bể là: chiều dài là $1,5m$; chiều rộng $1,2m$, chiều cao \(2m\). Mặt nước cách miệng bể \(0,5m\). Người ta mở khóa cho nước chảy ra khỏi bể, sau \(5\) giờ thì bể cạn. Hỏi nước chảy ra khỏi bể mỗi phút được bao nhiêu lít?
A. \(3\) lít
B. \(6\) lít
C. \(9\) lít
D. \(12\) lít
C. \(9\) lít
- Vì mặt nước cách miệng bể \(0,5m\) nên tính chiều cao mực nước trong bể ta lấy chiều cao của bể trừ đi \(0,5m\).
- Tính thể tích nước đang có trong bể ta lấy chiều dài nhân chiều rộng rồi nhân với chiều cao mực nước.
- Tính thể tích nước chảy ra trong \(1\) giờ ta lấy thể tích nước chia cho 5.
- Đổi thể tích nước chảy ra trong \(1\) giờ sang đơn vị đề-xi-mét khối, từ đó tìm được số lít nước chảy ra trong \(1\) giờ.
- Đổi \(1\) giờ $ = 60$ phút.
Để tìm số lít nước chảy ra trong \(1\) phút ta lấy số lít nước chảy ra trong \(1\) giờ chia cho \(60\).
Chiều cao mực nước trong bể là:
\(2 - 0,5 = 1,5\;(m)\)
Thể tích nước đang có trong bể
\(1,5 \times 1,2 \times 1,5 = 2,7\;({m^3})\)
Thể tích nước chảy ra trong \(1\) giờ là:
\(2,7:5 = 0,54\;({m^3})\)
Đổi \(0,54{m^3} = 540d{m^3} = 540\) lít; \(1\) giờ $ = 60$ phút
Mỗi phút nước chảy ra khỏi bể số lít là:
\(540:60 = 9\) (lít)
Đáp số: \(9\) lít.
- Có thể đổi các kích thước của bể nước sang đơn vị đo là đề-xi-mét rồi tìm thể tích nước với đơn vị đề-xi-mét khối (hay lít) sau đó tìm lượng nước trong bể.
- Học sinh có thể tính sai thể tích nước đang có trong bể khi xác định chiều cao mực nước là \(0,5m\).

Phân số \(\dfrac{5}{{100}}\) được viết dưới dạng số thập phân là:
A. \(0,5\)
B. \(0,05\)
C. \(0,005\)
D. \(0,0005\)
B. \(0,05\)
Sử dụng mẹo: Khi chuyển phân số thập phân thành số thập phân, ta đếm xem mẫu số có bao nhiêu chữ số \(0\) thì phần thập phân của số thập phân cũng có bấy nhiêu chữ số.
Phân số thập phân \(\dfrac{5}{{100}}\) có \(2\) chữ số \(0\) ở mẫu số nên phần thập phân của số thập phân sẽ có \(2\) chữ số, ta đếm từ phải sang trái, có \(5\) là một chữ số nên ta phải thêm \(1\) số \(0\) trước số \(5\) để có đủ \(2\) chữ số rồi đặt dấu phẩy trước số \(0\) vừa thêm, sau đó thêm \(0\) trước dấu phẩy.
Vậy \(\dfrac{5}{{100}} = 0,05\).

Trong bảng đơn vị đo diện tích, đơn vị lớn gấp bao nhiêu lần đơn vị bé tiếp liền?
A. \(10\) lần
B. \(100\) lần
C. \(1000\) lần
D. \(10000\) lần
B. \(100\) lần
Xem lại bảng đơn vị đo diện tích.
Trong bảng đơn vị đo diện tích, đơn vị lớn gấp \(100\) lần đơn vị bé tiếp liền.
Học sinh có thể nhớ nhầm sang bảng đơn vị đo độ dài nên chọn đáp án sai là A hoặc đơn vị đo thể tích nên chọn đáp án sai là C.

Điền dấu (\(>;\, <;\, =\)) thích hợp vào ô trống:
\(15{m^3}\;27d{m^3}\,\,\)
\(\,\,15,027{m^3}\)
\(15{m^3}\;27d{m^3}\,\,\)
\(\,\,15,027{m^3}\)
- Đưa hai số đo về cùng một dạng là dạng số thập phân.
- Xác định các số đo đã cùng đơn vị đo chưa, nếu không cùng đơn vị đo ta phải đổi thành cùng 1 đơn vị đo.
- Xác định các phần nguyên và phần thập phân để so sánh bình thường như so sánh các số thập phân.
Hai số đã cho chưa cùng đơn vị đo, ta sẽ đưa về cùng dạng số thập phân có đơn vị đo là \({m^3}\).
Ta có \(15{m^3}\,27d{m^3}\, = 15\dfrac{{27}}{{1000}}{m^3}\, = \,15,027{m^3}\)
Mà \(15,027{m^3} = 15,027{m^3}\)
Vậy \(15{m^3}\,27d{m^3}\, = \,15,027{m^3}\).

Điền số thích hợp vào ô trống:
\(667724 + 69058=\)
\(667724 + 69058=\)
- Đặt tính theo cột dọc sao cho các số cùng hàng thẳng cột với nhau.
- Cộng nhẩm từng hàng từ phải sang trái, từ hàng đơn vị rồi mới đến các hàng tiếp theo.
Đặt tính rồi thực hiện tính ta có:
\(\dfrac{{ + \begin{array}{*{20}{r}}{667724}\\{69058}\end{array}}}{{\,\,\,\,736782}}\)
Vậy \(667724 + 69058 = 736782\).
Đáp án đúng điền vào ô trống là \(736782\).

Điền số thích hợp vào ô trống:
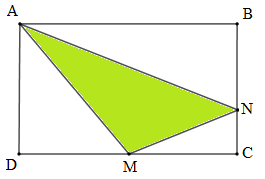
Cho hình vẽ như sau:

Biết hình chữ nhật $ABCD$ có diện tích bằng \(96c{m^2};{\rm{ }}MC{\rm{ }} = {\rm{ }}MD;\,\,BN = \dfrac{2}{3}BC\) (như hình vẽ).
Diện tích tam giác $AMN$ là
\(cm^2\).
Cho hình vẽ như sau:

Biết hình chữ nhật $ABCD$ có diện tích bằng \(96c{m^2};{\rm{ }}MC{\rm{ }} = {\rm{ }}MD;\,\,BN = \dfrac{2}{3}BC\) (như hình vẽ).
Diện tích tam giác $AMN$ là
\(cm^2\).
Diện tích tam giác $AMN$ bằng diện tích hình chữ nhật $ABCD$ trừ đi tổng diện tích ba tam giác vuông \(ABN,MNC,ADM\).
- Tính diện tích tam giác \(ADM\):
\({S_{ADM}} = \dfrac{1}{2} \times AD \times DM = \dfrac{1}{2} \times AD \times \dfrac{{DC}}{2} = \dfrac{1}{4} \times AD \times DC\)
Từ đó suy ra diện tích tam giác \(ADM\) bằng \(\dfrac{1}{4}\) diện tích hình chữ nhật $ABCD$.
- Tương tự ta tính được diện tích hai tam giác \(ABN,\,MNC\).
Theo đề bài:
\(\begin{array}{l}MC{\rm{ }} = {\rm{ }}MD \Rightarrow MC = MD = \dfrac{1}{2}DC\\BN = \dfrac{2}{3}BC \Rightarrow NC = \dfrac{1}{3}BC\end{array}\)
Ta có:
+) \({S_{ADM}} = \dfrac{1}{2} \times AD \times DM = \dfrac{1}{2} \times AD \times \dfrac{{DC}}{2} = \dfrac{1}{4} \times AD \times DC\)
Suy ra diện tích tam giác \(ADM\) bằng \(\dfrac{1}{4}\) diện tích hình chữ nhật $ABCD$.
Diện tích tam giác \(ADM\) là:
\(96:4 = 24\;(c{m^2})\)
+) \({S_{ABN}} = \dfrac{1}{2} \times AB \times BN = \dfrac{1}{2} \times AB \times \dfrac{2}{3}BC = \dfrac{1}{3} \times AB \times BC\)
Suy ra diện tích tam giác \(ABN\) bằng \(\dfrac{1}{3}\) diện tích hình chữ nhật $ABCD$.
Diện tích tam giác \(ABN\) là:
\(96:3 = 32\;(c{m^2})\)
+) \({S_{MNC}} = \dfrac{1}{2} \times MC \times NC = \dfrac{1}{2} \times \dfrac{1}{2}DC \times \dfrac{1}{3}BC = \dfrac{1}{{12}} \times DC \times BC\)
Suy ra diện tích tam giác \(MNC\) bằng \(\dfrac{1}{{12}}\) diện tích hình chữ nhật $ABCD$.
Diện tích tam giác \(MNC\)là:
\(96:12 = 8\;(c{m^2})\)
Diện tích tam giác \(AMN\)là:
\(96 - (24 + 32 + 8) = 32\;(c{m^2})\)
Đáp số: \(32c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(32\).

Điền số thích hợp vào ô trống:
Một bể nước dạng hình hộp chữ nhật có kích thước ở trong lòng bể là: chiều dài \(2,5m\), chiều rộng \(1,5m\) và chiều cao \(1,8m\). Khi bể không có nước người ta mở vòi cho nước chảy vào bể, mỗi giờ được \(750\) lít nước.
Vậy bể sẽ đầy nước sau
giờ.
Một bể nước dạng hình hộp chữ nhật có kích thước ở trong lòng bể là: chiều dài \(2,5m\), chiều rộng \(1,5m\) và chiều cao \(1,8m\). Khi bể không có nước người ta mở vòi cho nước chảy vào bể, mỗi giờ được \(750\) lít nước.
Vậy bể sẽ đầy nước sau
giờ.
Thể tích nước khi bể đầy nước chính là thể thể tích của hình hộp chữ nhật có chiều dài $2,5m$ ; chiều rộng $1,5m$ và chiều cao $1,8m$.
Để giải bài ta có thể làm như sau:
- Tính thể tích bể nước đó theo công thức: Thể tích = Chiều dài × chiều rộng × chiều cao.
- Đổi thể tích từ đơn vị mét khối sang đơn vị đề-xi-mét khối rồi tính số lít nước.
- Tính số giờ bơm nước vào bể ta lấy thể tích khi bể đầy nước chia cho số lít nước chảy vào bể trong \(1\) giờ.
Thể tích của bể nước là:
\(2,5 \times 1,5 \times 1,8 = 6,75({m^3})\)
Đổi \(6,75{m^3} = 6750d{m^3} = 6750\) lít
Bể đầy nước sau số giờ là:
\(6750:750 = 9\) (giờ)
Đáp số: \(9\) giờ.
Vậy đáp án đúng điền vào ô trống là \(9\).
- Có thể đổi số lít nước chảy vào bể trong \(1\) giờ sang đơn vị đề-xi-mét khối rồi đổi tiếp sang đơn vị mét khối. Tính số giờ bơm nước vào bể ta lấy thể tích khi bể đầy nước theo đơn vị mét khối chia cho số mét khối nước chảy vào bể trong \(1\) giờ.

Điền số thích hợp vào ô trống:
\(45\) phút \(15\) giây \( - \,17\) phút \(28\) giây \( = \)
phút
giây.
\(45\) phút \(15\) giây \( - \,17\) phút \(28\) giây \( = \)
phút
giây.
- Đặt tính thẳng hàng và thực hiện tính như đối với phép trừ các số tự nhiên.
- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.
- Nếu số đo theo đơn vị nào đó ở số bị trừ bé hơn số đo tương ứng ở số trừ thì cần chuyển đổi $1$ đơn vị hàng lớn hơn liền kề sang đơn vị nhỏ hơn rồi thực hiện phép trừ như bình thường .
Ta đặt tính và thực hiện tính như sau:

Vậy \(45\) phút \(15\) giây \( - \,\,17\) phút \(28\) giây \( = \,\,27\) phút \(47\) giây.
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(27\,;\,\,47\).

Một ô tô đi từ tỉnh A lúc \(7\) giờ \(40\) phút và đến tỉnh B lúc \(10\) giờ \(4\) phút với vận tốc \(45\)km/giờ. Đến tỉnh B ô tô nghỉ \(45\) phút để lấy hàng rồi quay trở về tỉnh A. Hỏi ô tô trở về A lúc mấy giờ? Biết vận tốc ô tô khi quay về tỉnh A là \(48\)km/giờ.
A. \(\,12\) giờ \(19\) phút
B. \(\,13\) giờ \(4\) phút
C. \(\,13\) giờ \(24\) phút
D. \(\,12\) giờ \(45\) phút
B. \(\,13\) giờ \(4\) phút
- Tính thời gian ô tô đi từ A đến B \(=\) thời gian lúc ô tô đến B \(-\) thời gian lúc ô tô đi từ A.
- Đổi số đo thời gian vừa tìm được sang dạng số thập phân có đơn vị là giờ.
- Tính độ dài quãng đường AB ta lấy vận tốc nhân với thời gian.
- Tính thời gian lúc ô tô bắt đầu từ B về A \(=\) thời gian lúc ô tô đến B \(+\) thời gian ô tô nghỉ để lấy hàng.
- Tính thời gian ô tô đi từ B về A ta lấy quãng đường chia cho vận tốc.
- Đổi số đo thời gian vừa tìm được sang dạng số tự nhiên.
- Tính thời gian lúc ô tô về đến A \(=\) thời gian lúc ô tô từ B bắt đầu từ B về \(+\) thời gian ô tô đi từ B về A.
Ô tô đi từ A đến B hết số thời gian là:
\(10\) giờ \(4\) phút \( - \,7\) giờ \(40\) phút \( = \,2\) giờ \(24\) phút
Đổi \(\,2\) giờ \(24\) phút \( = \,2,4\) giờ
Quãng đường AB dài là:
\(45 \times 2,4 = 108\;(km)\)
Ô tô bắt đầu đi từ B về A lúc:
\(10\) giờ \(4\) phút \( + \,45\) phút \( = \,10\) giờ \(49\) phút
Ô tô đi từ B về A hết số thời gian là:
\(108:48 = 2,25\) (giờ)
Đổi \(2,25\) giờ \( = \,2\) giờ \(15\) phút
Ô tô về đến A lúc:
\(\,10\) giờ \(49\) phút \( + \,2\) giờ \(15\) phút \( = \,12\) giờ \(64\) phút
Đổi \(\,12\) giờ \(64\) phút \( = \,13\) giờ \(4\) phút
Đáp số: \(\,13\) giờ \(4\) phút.
- Có thể tính “gộp”:
Tính thời gian lúc ô tô về đến A \(=\) thời gian lúc ô tô đến B \(+\) thời gian ô tô nghỉ để lấy hàng \(+\) thời gian ô tô đi từ B về A.
- Học sinh có thể tính sai thời gian khi ô tô trở về A khi không cộng thêm thời gian ô tô nghỉ để lấy hàng.

Điền số thích hợp vào ô trống:
Một cửa hàng bán đường trong ba ngày, trung bình mỗi ngày cửa hàng bán được \(4\) tạ đường. Ngày đầu cửa hàng bán được \(468kg\) đường, ngày thứ hai cửa hàng bán được \(75\% \) số đường bán được trong ngày đầu.
Vậy ngày thứ ba cửa hàng bán được
ki-lô-gam đường.
Một cửa hàng bán đường trong ba ngày, trung bình mỗi ngày cửa hàng bán được \(4\) tạ đường. Ngày đầu cửa hàng bán được \(468kg\) đường, ngày thứ hai cửa hàng bán được \(75\% \) số đường bán được trong ngày đầu.
Vậy ngày thứ ba cửa hàng bán được
ki-lô-gam đường.
- Tìm số đường bán được bán được trong ba ngày theo công thức:
Tổng \( = \) trung bình cộng \( \times \) số số hạng
- Đổi khối lượng đường vừa tìm được sang đơn vị ki-lô-gam.
- Tìm số đường bán được trong ngày thứ hai, tức là tìm \(75\% \) của \(468kg\), ta lấy \(468kg\) chia cho \(100\) rồi nhân với \(75.\)
- Tìm số đường bán đươc trong ngày thứ ba ta lấy tổng số đường bán trong ba ngày trừ đi tổng số đường bán trong hai ngày đầu.
Trong ba ngày, cửa hàng bán được số đường là:
\(4 \times 3 = 12\) (tạ)
Đổi \(12\) tạ $= 1200kg$.
Ngày thứ hai cửa hàng bán được số ki-lô-gam đường là:
\(468:100 \times 75 = 351(kg)\)
Ngày thứ ba cửa hàng bán số ki-lô-gam đường là:
$1200 - (468 + 351) = 381 (kg)$
Đáp số: \(381kg\) đường.
Vậy đáp án đúng điền vào ô trống là \(381\).
Học sinh có thể làm sai khi tìm số đường bán được trong ngày thứ hai bằng \(468:75 \times 100 = 624(kg)\), từ đó tìm được số đường bán trong ngày thứ ba là \(208kg\).

Điền số thích hợp vào ô trống:
Một ô tô du lịch khởi hành từ A lúc \(5\) giờ \(40\) phút để đi về B. Cùng lúc đó một ô tô chở hàng đi từ B về A. Hai ô tô gặp nhau lúc \(8\) giờ \(30\) phút. Quãng đường AB dài \(306km\) và vận tốc ô tô du lịch bằng \(\dfrac{4}{5}\) vận tốc ô tô chở hàng.
Vậy vận tốc của ô tô du lịch là
km/giờ, vận tốc của ô tô chở hàng là
km/giờ.
Một ô tô du lịch khởi hành từ A lúc \(5\) giờ \(40\) phút để đi về B. Cùng lúc đó một ô tô chở hàng đi từ B về A. Hai ô tô gặp nhau lúc \(8\) giờ \(30\) phút. Quãng đường AB dài \(306km\) và vận tốc ô tô du lịch bằng \(\dfrac{4}{5}\) vận tốc ô tô chở hàng.
Vậy vận tốc của ô tô du lịch là
km/giờ, vận tốc của ô tô chở hàng là
km/giờ.
Theo đề bài, hai xe xuất phát cùng lúc. Để giải bài này ta làm như sau:
- Tính thời gian đi để gặp nhau ta lấy thời gian lúc gặp nhau trừ đi thời gian lúc hai ô tô xuất phát: $8$ giờ \(30\) phút $ - \,5$ giờ \(40\) phút và đổi kết quả vừa tìm được sang dạng số thập phân hoặc phân số có đơn vị là giờ.
- Tính tổng vận tốc hai xe ta lấy quãng đường AB chia cho thời gian đi để gặp nhau.
- Giải bài toán tìm hai số khi biết tổng và tỉ số của hai số. Theo đề bài, vận tốc ô tô du lịch bằng \(\dfrac{4}{5}\) vận tốc ô tô chở hàng nên ta vẽ sơ đồ biểu thị vận tốc ô tô du lịch gồm \(4\) phần bằng nhau, vận tốc ô tô chở hàng gồm 5 phần như thế. Để tìm hai số ta áp dụng công thức sau:
Số bé \(=\) (tổng : tổng số phần bằng nhau) \( \times \) số phần của số bé;
Số lớn \(=\) (tổng : tổng số phần bằng nhau) \( \times \) số phần của số lớn.
Ta có sơ đồ chuyển động của hai xe:
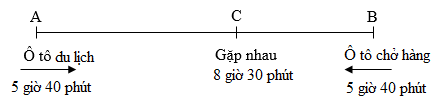
Thời gian đi để hai xe gặp nhau là:
$8$ giờ \(30\) phút $ - \,5$ giờ \(40\) phút $ = 2$ giờ \(50\) phút
Đổi $2$ giờ $50$ phút \( = \,2\dfrac{5}{6}\) giờ\( = \,\dfrac{{17}}{6}\) giờ
Tổng vận tốc của hai xe là:
\(306:\dfrac{{17}}{6} = 108\)(km/giờ)
Ta có sơ đồ:
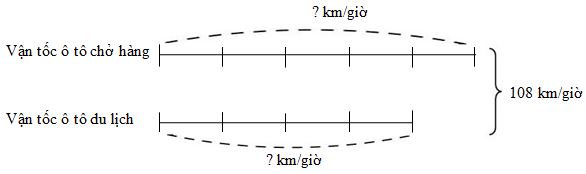
Theo sơ đồ, tổng số phần bằng nhau là:
\(5 + 4 = 9\) (phần)
Vận tốc ô tô chở hàng là:
\(108:9 \times 5 = 60\) (km/giờ)
Vận tốc ô tô du lịch là:
\(108 - 60 = 48\) (km/giờ)
Đáp số: Ô tô du lịch: \(48\) km/giờ;
Ô tô chở hàng: \(60\) km/giờ.
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trên xuống dưới, từ trái sang phải là \(48\,;\,\,60\).
Học sinh cần chú ý tính đúng thời gian đi để gặp nhau, từ đó mới tính đúng tổng vận tốc của hai ô tô.

Tính giá trị biểu thức: \(50 - 22,5:12,5 + 36,5:10\).
A. \(3,87\)
B. \(5,85\)
C. \(51,67\)
D. \(51,85\)
D. \(51,85\)
- Biểu thức có chứa phép cộng, phép trừ và phép chia nên ta thực hiện phép tính chia trước, tính phép cộng, trừ sau.
- Khi biểu thức chỉ chứa phép tính cộng và trừ, ta tính lần lượt từ trái sang phải.
Ta có:
\(\begin{array}{l}50 - 22,5:12,5 + 36,5:10 \\ = 50 - 1,8 + 3,65\\ = 48,2 + 3,65\\ = 51,85\end{array}\)
Vậy giá trị của biểu thức \(50 - 22,5:12,5 + 36,5:10\) là \(51,85\).
- Học sinh sinh có thể làm sai khi tính lần lượt từ trái sang phải, từ đó chọn đáp án sai là A.
- Học sinh có thể sai khi tính \((50 - 22,5):12,5\) sau đó cộng với kết quả phép tính \(36,5:10\), từ đó chọn đáp án sai là B.
- Một số tính sai bước cuối, tính \(48,2 + 3,65 = 51,67\) nên chọn đáp án sai là D.
>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 5 trên Tuyensinh247.com. Cam kết giúp con lớp 5 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |









