Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Bài 3. Các hệ thức lượng trong tam giác và giải tam giác
Câu hỏi 5 trang 50 SGK Hình học 10
Cho tam giác ABC vuông ở A nội tiếp trong đường tròn bán kính R và có BC = a, CA = b, AB = c....
Đề bài
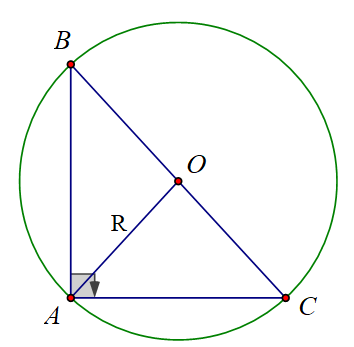
Cho tam giác ABC vuông ở A nội tiếp trong đường tròn bán kính R và có BC = a, CA = b, AB = c.
Chứng minh hệ thức: \({a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = 2R\)
Video hướng dẫn giải
Lời giải chi tiết
Do tam giác ABC vuông tại A nên trung điểm O của BC là tâm đường tròn ngoại tiếp tam giác ABC ⇒ BC = a = 2R
Ta có:
\(\eqalign{
& \sin A = \sin {90^0} = 1 = {a \over a} = {a \over {2R}} \cr
& \Rightarrow {a \over {\sin A}} = 2R \cr
& \sin B = {b \over a} = {b \over {2R}} \Rightarrow {b \over {\sin B}} = 2R \cr
& \sin C = {c \over a} = {c \over {2R}} \Rightarrow {c \over {\sin C}} = 2R \cr} \)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu hỏi 6 trang 52 SGK Hình học 10
- Câu hỏi 7 trang 53 SGK Hình học 10
- Câu hỏi 8 trang 54 SGK Hình học 10
- Câu hỏi 9 trang 54 SGK Hình học 10
- Bài 1 trang 59 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
