 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Ôn tập chương VI - Cung và góc lượng giác. Công thức lư..
Ôn tập chương VI - Cung và góc lượng giác. Công thức lư..
Bài 4 trang 155 SGK Đại số 10
Rút gọn biểu thức
Video hướng dẫn giải
Rút gọn biểu thức
LG a
\(\displaystyle {{2\sin 2\alpha - \sin 4\alpha } \over {2\sin 2\alpha + \sin 4\alpha }}\)
Phương pháp giải:
Áp dụng các công thức:
\(\begin{array}{l}
+ )\cos2\alpha = 1 - 2{\sin ^2}\alpha = 2{\cos ^2}\alpha - 1.\\
+ )\tan\alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}.\\
+ )\tan\alpha .\cot\alpha = 1.
\end{array}\)
Lời giải chi tiết:
\(\eqalign{ & {{2\sin 2\alpha - \sin 4\alpha } \over {2\sin 2\alpha + \sin 4\alpha }} \cr& = \frac{{2\sin 2\alpha - \sin \left( {2.2\alpha } \right)}}{{2\sin 2\alpha + \sin \left( {2.2\alpha } \right)}}\cr&= {{2\sin 2\alpha - 2\sin 2\alpha .cos2\alpha } \over {2\sin 2\alpha + 2\sin 2\alpha .cos2\alpha }} \cr & = \frac{{2\sin 2\alpha \left( {1 - \cos 2\alpha } \right)}}{{2\sin 2\alpha \left( {1 + \cos 2\alpha } \right)}}\cr &= {{1 - \cos 2\alpha } \over {1 + \cos 2\alpha }} = \frac{{1 - \left( {1 - 2{{\sin }^2}\alpha } \right)}}{{1 + \left( {2{{\cos }^2}\alpha - 1} \right)}}\cr&= {{2{{\sin }^2}\alpha } \over {2{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}\cr&={\left( {\frac{{\sin \alpha }}{{\cos \alpha }}} \right)^2}=\tan^2\alpha.\cr} \)
LG b
\(\tan \alpha ({{1 + {{\cos }^2}\alpha } \over {\sin \alpha }} - \sin \alpha )\)
Lời giải chi tiết:
\(\eqalign{& \tan \alpha \left({{1 + {{\cos }^2}\alpha } \over {\sin \alpha }} - \sin \alpha\right ) \cr&= {{\sin \alpha } \over {\cos \alpha }}\left({{1 + {{\cos }^2}\alpha - {{\sin }^2}\alpha } \over {\sin \alpha }}\right) \cr & = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha + {{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\sin \alpha }}\cr &= {{\sin \alpha } \over {\cos \alpha }}.{{2{{\cos }^2}\alpha } \over {\sin \alpha }} = 2\cos \alpha. \cr} \)
LG c
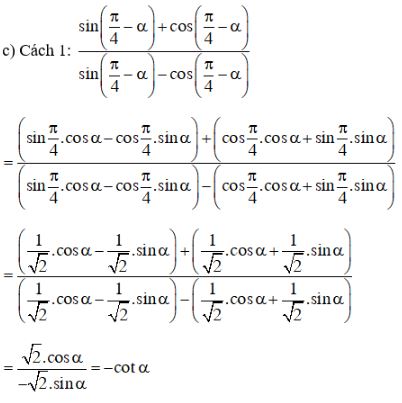
\(\displaystyle {{\sin ({\pi \over 4} - \alpha ) + \cos ({\pi \over 4} - \alpha )} \over {\sin ({\pi \over 4} - \alpha ) - \cos ({\pi \over 4} - \alpha )}}\)
Lời giải chi tiết:
\(\displaystyle {{\sin ({\pi \over 4} - \alpha ) + \cos ({\pi \over 4} - \alpha )} \over {\sin ({\pi \over 4} - \alpha ) - \cos ({\pi \over 4} - \alpha )}}\)
\(\begin{array}{l}
= \dfrac{{\cos \left( {\frac{\pi }{4} - \alpha } \right)\left[ {\frac{{\sin \left( {\frac{\pi }{4} - \alpha } \right)}}{{\cos \left( {\frac{\pi }{4} - \alpha } \right)}} + 1} \right]}}{{\cos \left( {\frac{\pi }{4} - \alpha } \right)\left[ {\frac{{\sin \left( {\frac{\pi }{4} - \alpha } \right)}}{{\cos \left( {\frac{\pi }{4} - \alpha } \right)}} - 1} \right]}}\\
= \dfrac{{\cos \left( {\frac{\pi }{4} - \alpha } \right)\left[ {\tan \left( {\frac{\pi }{4} - \alpha } \right) + 1} \right]}}{{\cos \left( {\frac{\pi }{4} - \alpha } \right)\left[ {\tan \left( {\frac{\pi }{4} - \alpha } \right) - 1} \right]}}\\
= \dfrac{{\tan \left( {\frac{\pi }{4} - \alpha } \right) + 1}}{{\tan \left( {\frac{\pi }{4} - \alpha } \right) - 1}}\\
= \left[ {\tan \left( {\frac{\pi }{4} - \alpha } \right) + 1} \right]:\left[ {\tan \left( {\frac{\pi }{4} - \alpha } \right) - 1} \right]\\
= \left( {\frac{{\tan \frac{\pi }{4} - \tan \alpha }}{{1 + \tan \frac{\pi }{4}.\tan \alpha }} + 1} \right)
:\left( {\frac{{\tan \frac{\pi }{4} - \tan \alpha }}{{1 + \tan \frac{\pi }{4}.\tan \alpha }} - 1} \right)\\
= \left( {\frac{{1 - \tan \alpha }}{{1 + \tan \alpha }} + 1} \right):\left( {\frac{{1 - \tan \alpha }}{{1 + \tan \alpha }} - 1} \right)\\
= \frac{{1 - \tan \alpha + 1 + \tan \alpha }}{{1 + \tan \alpha }}:\frac{{1 - \tan \alpha - 1 - \tan \alpha }}{{1 + \tan \alpha }}\\
= \frac{2}{{1 + \tan \alpha }}:\frac{{ - 2\tan \alpha }}{{1 + \tan \alpha }}\\
= \frac{2}{{1 + \tan \alpha }}.\frac{{1 + \tan \alpha }}{{ - 2\tan \alpha }}\\
= - \frac{1}{{\tan \alpha }} = - \cot \alpha
\end{array}\)
Cách khác:
LG d
\(\displaystyle {{\sin 5\alpha - \sin 3\alpha } \over {2\cos 4\alpha }}\)
Lời giải chi tiết:
\(\displaystyle {{\sin 5\alpha - \sin 3\alpha } \over {2\cos 4\alpha }} \) \(\displaystyle = {{2\cos {{5\alpha + 3\alpha } \over 2}\sin {{5\alpha - 3\alpha } \over 2}} \over {2\cos 4\alpha }} \) \(\displaystyle = \frac{{2\cos 4\alpha \sin \alpha }}{{2\cos 4\alpha }}\)
\(\displaystyle = \sin \alpha \)
Loigiaihay.com




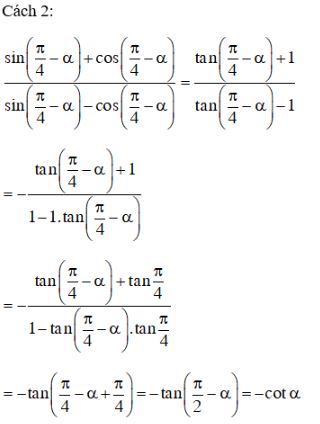









Danh sách bình luận