Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Ôn tập chương II - Hàm số bậc nhất và bậc hai
Bài 10 trang 51 SGK Đại số 10
Lập bảng biến thiên và vẽ đồ thị của hàm số
Video hướng dẫn giải
Lập bảng biến thiên và vẽ đồ thị của hàm số
LG a
\(y = x^2– 2x – 1\)
Phương pháp giải:
Sử dụng các bảng biến thiên của hàm số bậc hai và đồ thị của hàm số trong các trường hợp \(a<0\) và \(a>0\). Xem tại đây.
Lời giải chi tiết:
Hàm số y = x2 – 2x – 1 có a = 1 > 0 ; b = –2 ; c = –1;
\(\Delta = {\left( { - 2} \right)^2} - 4.1.\left( { - 1} \right) = 8\)
+ Tập xác định D = R.
\(\begin{array}{l}
- \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1\\
- \frac{\Delta }{{4a}} = - \frac{8}{{4.1}}= - 2
\end{array}\)
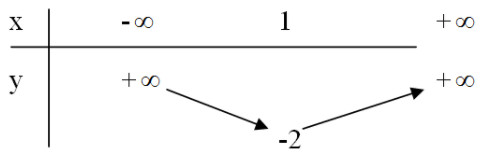
+ Hàm số nghịch biến trên (–∞ ; 1) ; đồng biến trên (1 ; + ∞).
Bảng biến thiên
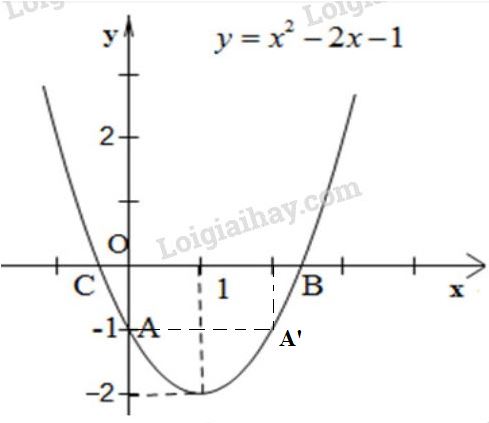
Đồ thị hàm số
Đồ thị là parabol có bề lõm hướng lên trên.
+ Đỉnh \(I(1; -2)\) với trục đối xứng \(x = 1\)
+ Giao điểm với trục tung là \(A(0;-1)\)
+ Điểm đối xứng với A qua đường thẳng x = 1 là A'(2 ; –1).
+ Giao điểm với trục hoành \(C (1-\sqrt2; 0)\) và \(B((1+\sqrt2; 0)\)
LG b
\(y = -x^2+ 3x + 2\)
Phương pháp giải:
Sử dụng các bảng biến thiên của hàm số bậc hai và đồ thị của hàm số trong các trường hợp \(a<0\) và \(a>0\). Xem tại đây.
Lời giải chi tiết:
\(y = -x^2+ 3x + 2\)
a=-1 < 0, b=3, c=2
\(\Delta = {3^2} - 4.\left( { - 1} \right).2 = 17\)
Tập xác định \(D =\mathbb R\)
\(\begin{array}{l}
- \frac{b}{{2a}} = - \frac{3}{{2.\left( { - 1} \right)}} = \frac{3}{2}\\
- \frac{\Delta }{{4a}} = - \frac{{17}}{{4.\left( { - 1} \right)}}= \frac{{17}}{4}
\end{array}\)
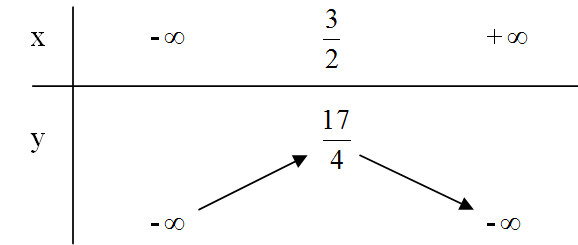
Hàm số đồng biến trên \(\left( { - \infty ;\frac{3}{2}} \right)\) và nghịch biến trên \(\left( {\frac{3}{2}; + \infty } \right)\)
Bảng biến thiên:
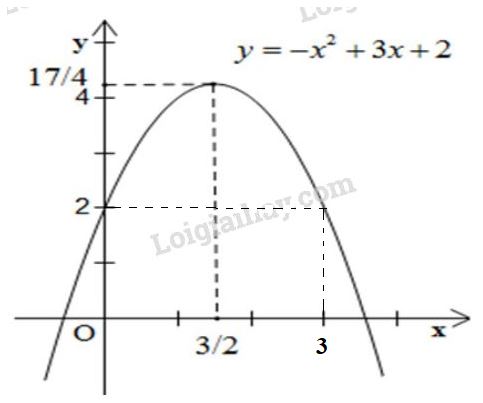
Đồ thị hàm số
Đồ thị: parabol có bề lõm hướng xuống dưới
+ Đỉnh \(I \left({3 \over 2}; \, {{17} \over 4}\right)\)
+ Trục đối xứng \(x ={3 \over 2}\)
+ Giao điểm với trục tung là \(A(0; \, 2)\)
+ Điểm đối xứng với A qua đường thẳng x = 3/2 là A'(3 ; 2).
+ Giao điểm với trục hoành \( C \left({{3 - \sqrt {17} } \over 2}; \,0\right)\) và \(B\left({{3 + \sqrt {17} } \over 2}; \,0\right)\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 11 trang 51 SGK Đại số 10
- Bài 12 trang 51 SGK Đại số 10
- Bài 13 trang 51 SGK Đại số 10
- Bài 14 trang 51 SGK Đại số 10
- Bài 15 trang 51 SGK Đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
