 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Ôn tập chương II - Hàm số bậc nhất và bậc hai
Ôn tập chương II - Hàm số bậc nhất và bậc hai
Bài 8 trang 50 SGK Đại số 10
Tìm tập xác định của các hàm số
Video hướng dẫn giải
Tìm tập xác định của các hàm số
LG a
\(y = {2 \over {x + 1}} + \sqrt {x + 3}\)
Phương pháp giải:
+) Hàm số \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) xác định khi \(g(x) \neq 0.\)
+) Hàm số: \(y = \sqrt {f\left( x \right)} \) xác định khi \(f(x) \geq 0.\)
Lời giải chi tiết:
\(y = {2 \over {x + 1}} + \sqrt {x + 3}\)
Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l}
x + 1 \ne 0\\
x + 3 \ge 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \ne - 1\\
x \ge - 3
\end{array} \right..\)
Tập xác định: \(D = \left[ { - 3; + \infty } \right)\backslash \left\{ -1 \right\} \)\(= \left[ { - 3; - 1} \right) \cup \left( {-1; + \infty } \right).\)
LG b
\(y = \sqrt {2 - 3x} - {1 \over {\sqrt {1 - 2x} }}\)
Phương pháp giải:
+) Hàm số \(y = \frac{{f\left( x \right)}}{{\sqrt {g\left( x \right)} }}\) xác định khi \(g(x) > 0.\)
+) Hàm số: \(y = \sqrt {f\left( x \right)} \) xác định khi \(f(x) \geq 0.\)
Lời giải chi tiết:
\(y = \sqrt {2 - 3x} - {1 \over {\sqrt {1 - 2x} }}\)
Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l}
2 - 3x \ge 0\\
1 - 2x > 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
3x \le 2\\
2x < 1
\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}
x \le \frac{2}{3}\\
x < \frac{1}{2}
\end{array} \right. \Leftrightarrow x < \frac{1}{2}.\)
Tập xác định: \(D = \left( { - \infty ;\frac{1}{2}} \right).\)
Chú ý:
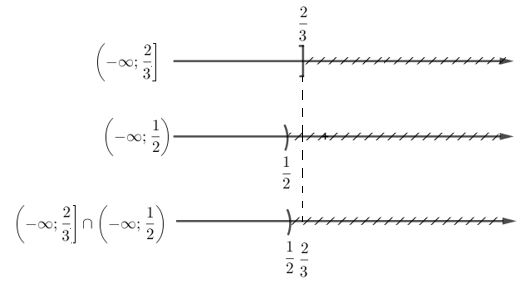
Các em dùng trục số để lấy giao hai tập hợp như sau:
LG c
\(y = \left\{ \matrix{{1 \over {x + 3}} \, \, khi \, \, x \ge 1 \hfill \cr \sqrt {2 - x} \, \, \, khi \, \, x < 1 \hfill \cr} \right.\)
Phương pháp giải:
+) Hàm số \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) xác định khi \(g(x) \neq 0.\)
+) Hàm số: \(y = \sqrt {f\left( x \right)} \) xác định khi \(f(x) \geq 0.\)
Lời giải chi tiết:
+ Xét trên \(\left[ {1; + \infty } \right)\) thì \(y = \frac{1}{{x + 3}}\)
Hàm số xác định khi x + 3 ≠ 0 (luôn thỏa mãn với mọi x ≥ 1).
Vậy hàm số luôn xác định trên [1; +∞).
+ Xét trên (–∞; 1) thì \(y = \sqrt {2 - x} \)
Hàm số xác định khi 2 – x ≥ 0 ⇔ x ≤ 2 (luôn thỏa mãn với mọi x < 1).
Vậy hàm số luôn xác định trên (–∞; 1).
Kết luận: Hàm số xác định trên R.
Cách trình bày khác:
\(y = \left\{ \matrix{{1 \over {x + 3}} \, \, khi \, \, x \ge 1 \hfill \cr \sqrt {2 - x} \, \, \, khi \, \, x < 1 \hfill \cr} \right.\)
Hàm số xác định \( \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x \ge 1\\
x + 3 \ne 0
\end{array} \right.\\
\left\{ \begin{array}{l}
x < 1\\
2 - x \ge 0
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x \ge 1\\
x \ne - 3
\end{array} \right.\\
\left\{ \begin{array}{l}
x < 1\\
x \le 2
\end{array} \right.
\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}
x \ge 1\\
x < 1
\end{array} \right..\)
\(\Leftrightarrow x\in R\).
Tập xác định: \(D = R.\)
Loigiaihay.com












Danh sách bình luận