Bài 2. Hai đường thẳng song song trong không gian Toán ..

Bài 4 trang 100 SGK Toán 11 tập 1 - Cánh diều

Cho tứ diện ABCD. Gọi ({G_1},{G_2}) lần lượt là trọng tâm của các tam giác ABC và ABD. Chứng minh rằng đường thẳng ({G_1}{G_2}) song song với đường thẳng CD.

Đề bài

Cho tứ diện ABCD. Gọi \({G_1},{G_2}\) lần lượt là trọng tâm của các tam giác ABC và ABD. Chứng minh rằng đường thẳng \({G_1}{G_2}\) song song với đường thẳng CD.

Phương pháp giải - Xem chi tiết

Áp dụng định lý Talet đảo

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Lời giải chi tiết

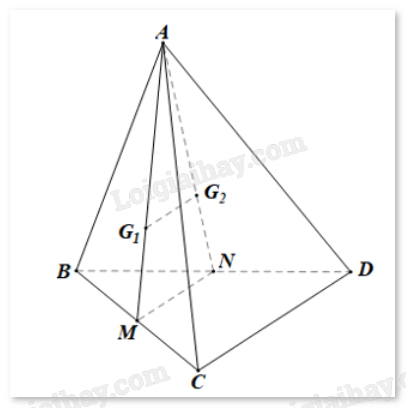
Trong mặt phẳng ABC, kẻ trung tuyến AM của tam giác ABC.

Vì \({G_1}\) là trọng tâm tam giác ABC nên \(\frac{{A{G_1}}}{{AM}} = \frac{2}{3}\).

Trong mặt phẳng ABD, kẻ trung tuyến AN của tam giác ABN.

Vì \({G_2}\) là trọng tâm tam giác ABC nên \(\frac{{A{G_2}}}{{AN}} = \frac{2}{3}\).

Xét tam giác AMN, có \(\frac{{A{G_1}}}{{AM}} = \frac{{A{G_2}}}{{AN}} = \frac{2}{3}\) nên \({G_1}{G_2}\)//MN (định lý Thales đảo).

Xét tam giác BCD có M, N lần lượt là trung điểm của BC, BD nên MN là đường trung bình.

Khi đó, MN//CD.

Vậy \({G_1}{G_2}\)//CD (cùng song song với MN).

Bình luận

Chia sẻ

Bình chọn:

4 trên 4 phiếu

Bài tiếp theo

Bài 5 trang 100 SGK Toán 11 tập 1 - Cánh diều
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và (AB = 2CD).Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD.
Bài 6 trang 100 SGK Toán 11 tập 1 - Cánh diều
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ. a) Chứng minh rằng bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành. b) Chứng minh rằng (IK//BC) c) Xác định giao tuyến của hai mặt phẳng (IJKL) và (SBC)
Bài 7 trang 100 SGK Toán 11 tập 1 - Cánh diều
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của các cạnh BC, CD. Trên cạnh AC lấy điểm K. Gọi M là giao điểm của BK và AI, N là giao điểm của DK và AJ. Chứng minh rằng đường thẳng MN song song với đường thẳng BD.
Bài 3 trang 100 SGK Toán 11 tập 1 - Cánh diều
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, AB, SD. Xác định giao tuyến của mỗi cặp mặt phẳng sau: (SAD) và (SBC); (MNP) và (ABCD).
Bài 2 trang 100 SGK Toán 11 tập 1 - Cánh diều
Quan sát Hình 43 và cho biết vị trí tương đối của hai trong ba cột tuabin gió có trong hình.
Bài 1 trang 100 SGK Toán 11 tập 1 - Cánh diều
Quan sát phòng học của lớp và nêu lên hình ảnh của hai đường thẳng song song, cắt nhau, chéo nhau.
Giải mục 2 trang 97, 98, 99, 100 SGK Toán 11 tập 1 - Cánh Diều
Trong không gian, cho điểm M và đường thẳng d không đi qua điểm M (Hình 36). Nêu dự đoán về số đường thẳng đi qua điểm M và song song với đường thẳng d.
Giải mục 1 trang 95, 96, 97 SGK Toán 11 tập 1 - Cánh Diều
a) Hãy nêu các vị trí tương đối của hai đường thẳng trong mặt phẳng. b) Quan sát hai đường thẳng a và b trong Hình 31a, 31b và cho biết các đường thẳng đó có cùng nằm trong một mặt phẳng không
Lý thuyết Hai đường thẳng song song trong không gian - SGK Toán 11 Cánh Diều
I. Vị trí tương đối của hai đường thẳng