Bài 5. Khoảng cách Toán 11 Cánh Diều

Lý thuyết Khoảng cách - Toán 11 Cánh diều

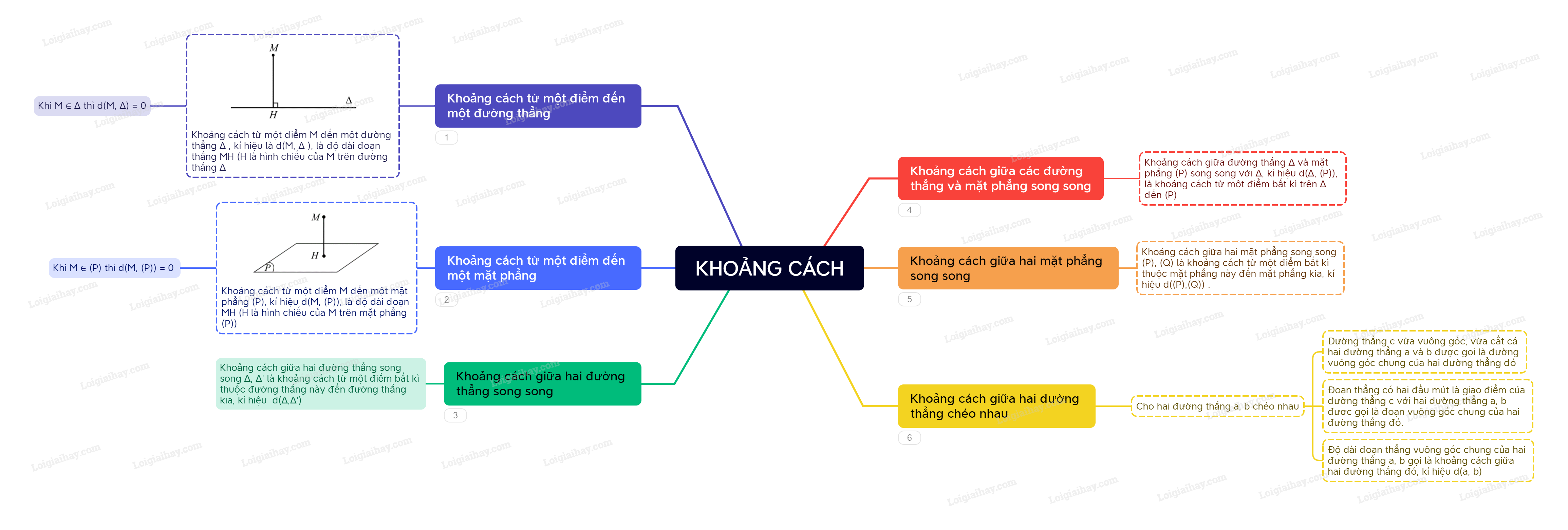
1. Khoảng cách từ một điểm đến một đường thẳng Cho đường thẳng \(\Delta \) và điểm \(M\) không thuộc \(\Delta \).

Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh

1. Khoảng cách từ một điểm đến một đường thẳng

Cho đường thẳng \(\Delta \) và điểm \(M\) không thuộc \(\Delta \). Gọi \(H\) là hình chiếu của điểm \(M\) trên đường thẳng \(\Delta \). Độ dài đoạn thẳng MH gọi là khoảng cách từ điểm \(M\) đến đường thẳng \(\Delta \), kí hiệu \(d(M,\Delta )\).

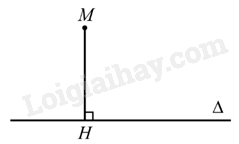
Chú ý: Khi điểm \(M\) thuộc đường thẳng \(\Delta \) thì \(d(M,\Delta ) = 0.\)

2. Khoảng cách từ một điểm đến một mặt phẳng

Cho mặt phẳng \((P)\) và điểm \(M\) không thuộc mặt phẳng \((P)\). Gọi \(H\) là hình chiếu của \(M\) trên mặt phẳng \((P)\). Độ dài đoạn thẳng MH gọi là khoảng cách từ điểm \(M\) đến mặt phẳng \((P)\), kí hiệu \(d(M,(P))\).

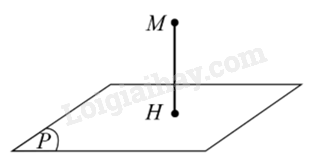
Chú ý: Khi điểm \(M\) thuộc mặt phẳng \((P)\) thì \(d(M,(P)) = 0.\)

3. Khoảng cách giữa hai đường thẳng song song

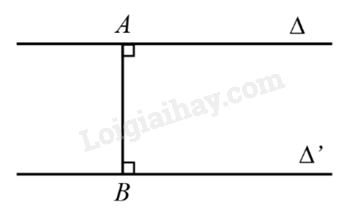
Khoảng cách giữa hai đường thẳng song song \(\Delta ,\Delta '\) là khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia, kí hiệu \(d\left( {\Delta ,{\Delta ^\prime }} \right)\).

Ví dụ: Trong hình dưới đây, ta có: \(d\left( {\Delta ,{\Delta ^\prime }} \right) = AB\) với \(A \in \Delta \), \(B \in {\Delta ^\prime },AB \bot \Delta ,AB \bot {\Delta ^\prime }\) và \(\Delta //{\Delta ^\prime }\).

4. Khoảng cách giữa đường thẳng và mặt phẳng song song

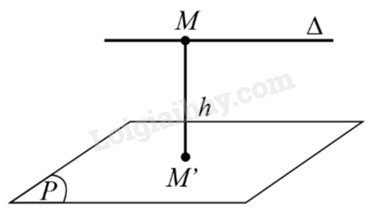
Cho đường thẳng \(\Delta \) song song với mặt phẳng \((P)\). Khoảng cách giữa đường thẳng \(\Delta \) và mặt phẳng \((P)\) là khoảng cách từ một điểm bất kì thuộc đường thẳng \(\Delta \) đến mặt phẳng \((P)\), kí hiệu \(d(\Delta ,(P))\).

Ví dụ: Trong hình dưới đây, ta có: \(d(\Delta ,(P)) = M{M^\prime } = h\), trong đó \(M \in \Delta ,{M^\prime } \in (P),M{M^\prime } \bot (P)\) và \(\Delta //(P)\).

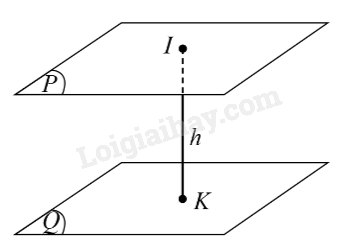
5. Khoảng cách giữa hai mặt phẳng song song

Khoảng cách giữa hai mặt phẳng song song \((P),(Q)\) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia, kí hiệu \(d((P),(Q))\).

Ví dụ: Trong hình dưới đây, ta có: \(d((P),(Q)) = IK = h\) với \(I \in (P),K \in (Q),IK \bot (P),IK \bot (Q)\) và \((P)//(Q)\).

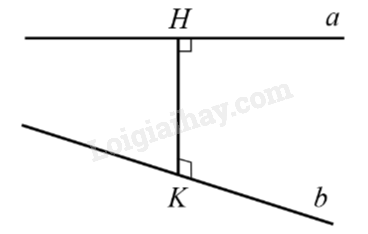
6. Khoảng cách giữa hai đưò̀ng thẳng chéo nhau

Cho hai đường thẳng a, b chéo nhau.

- Đường thẳng c vừa vuông góc, vừa cắt cả hai đường thẳng a và b được gọi là đường vuông góc chung của hai đường thẳng đó.

- Đoạn thẳng có hai đầu mút là giao điểm của đường thẳng c với hai đường thẳng a, b được gọi là đoạn vuông góc chung của hai đường thẳng đó.

- Độ dài đoạn thẳng vuông góc chung của hai đường thẳng a, b gọi là khoảng cách giữa hai đường thẳng đó, kí hiệu \(d(a,b)\).

Ví dụ: Trong hình dưới đây, ta có: \(d(a,b) = HK\) với HK là đoạn vuông góc chung của \(a\) và \(b\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 2 trang 100, 101 SGK Toán 11 tập 2 - Cánh Diều
Khi lắp thiết bị cho nhà bạn Nam, bác thợ khoan tường tại vị trí (M)
Giải mục 3 trang 102 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song (Delta ) và (Delta '). Xét điểm (A) trên đường thẳng (Delta ).
Giải mục 4 trang 102, 103 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\)
Giải mục 5 trang 103, 104 SGK Toán 11 tập 2 - Cánh Diều
a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song \(\left( P \right),\left( Q \right)\).
Giải mục 6 trang 10, 105, 106 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 73, khuôn cửa phía trên và mép cánh cửa phía dưới gợi nên hình ảnh hai đường thẳng \(a\)
Bài 1 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Hình 76 gợi nên hình ảnh hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau.
Bài 2 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Cho hình tứ diện \(ABCD\) có \(AB = a,BC = b,BD = c\),\(\widehat {ABC} = \widehat {ABD} = \widehat {BCD} = {90^ \circ }\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,AC,AD\) (Hình 77).
Bài 3 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Với giả thiết ở Bài tập 2, hãy:
Bài 4 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
Bài 5 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Với giả thiết ở Bài tập 4, hãy: