-
Toán 11 tập 1 - Cánh Diều
-
Giải Toán 11 tập 2 - Cánh Diều
Giải mục 3 trang 13, 14 SGK Toán 11 tập 1 - Cánh Diều
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác \(\left( {OA,OM} \right) = \alpha\), \(\left( {OA,OM'} \right) = - \alpha \) (Hình 13).
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
HĐ11
Trả lời câu hỏi Hoạt động 11 trang 13 SGK Toán 11 Cánh diều
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác \(\left( {OA,OM} \right) = \alpha\), \(\left( {OA,OM'} \right) = - \alpha \) (Hình 13).
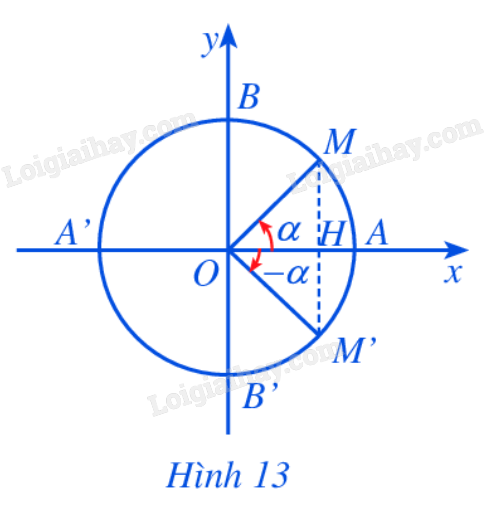
a) Nêu nhận xét về: hoành độ của chúng, tung độ của hai điểm M, M'.
b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \) và \(- \alpha \).
Phương pháp giải:
Dựa vào hình vẽ (Hình 13).
Lời giải chi tiết:
a) Hoành độ của điểm M và M’ bằng nhau.
Tung độ của điểm M và M’ đối nhau.
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha\) và \(- \alpha \).
LT-VD11
Trả lời câu hỏi Luyện tập - Vận dụng 11 trang 14 SGK Toán 11 Cánh diều
Tính:
a) \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8}\).
b) \(\tan {1^ \circ }.\tan {2^ \circ }.\tan {45^ \circ }.\tan {88^ \circ }.\tan {89^ \circ }\).
Phương pháp giải:
Sử dụng công thức trong bảng:
Lời giải chi tiết:
a) \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8} = {\cos ^2}\frac{\pi }{8} + {\cos ^2}\left( {\frac{\pi }{2} - \frac{\pi }{8}} \right)\)
\(= {\cos ^2}\frac{\pi }{8} + {\sin ^2}\frac{\pi }{8} = 1\).
b)
\(\begin{array}{l}\tan {1^ \circ }.\tan {2^ \circ }.\tan {45^ \circ }.\tan {88^ \circ }.\tan {89^ \circ }\\ = (\tan {1^ \circ }.\tan {89^ \circ }).(\tan {2^ \circ }.\tan {88^ \circ }).\tan {45^ \circ }\\ = (\tan {1^ \circ }.\cot {1^ \circ }).(\tan {2^ \circ }.\cot {2^ \circ }).\tan {45^ \circ }\\ = 1.\end{array}\)
Bình luận
Chia sẻ
- Giải mục 4 trang 14 SGK Toán 11 tập 1 - Cánh Diều
- Bài 6 trang 15 SGK Toán 11 tập 1 - Cánh diều
- Bài 5 trang 15 SGK Toán 11 tập 1 - Cánh diều
- Bài 4 trang 15 SGK Toán 11 tập 1 - Cánh diều
- Bài 3 trang 15 SGK Toán 11 tập 1 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
