-
Toán 11 tập 1 - Cánh Diều
-
Giải Toán 11 tập 2 - Cánh Diều
Giải mục 2 trang 97, 98, 99, 100 SGK Toán 11 tập 1 - Cánh Diều
Trong không gian, cho điểm M và đường thẳng d không đi qua điểm M (Hình 36). Nêu dự đoán về số đường thẳng đi qua điểm M và song song với đường thẳng d.
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 97 SGK Toán 11 Cánh diều
Trong không gian, cho điểm M và đường thẳng d không đi qua điểm M (Hình 36). Nêu dự đoán về số đường thẳng đi qua điểm M và song song với đường thẳng d.
Phương pháp giải:
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
Lời giải chi tiết:
Có một và chỉ một đường thẳng đi qua điểm M và song song với đường thẳng d.
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 85 SGK Toán 11 Cánh diều
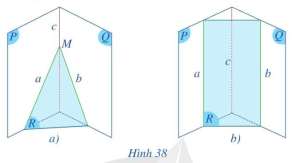
Cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó \(a = (P) \cap (R)\), \(b = (Q) \cap (R)\), \(c = (P) \cap (Q)\).
- Nếu hai đường thẳng a và b cắt nhau tại điểm M thì đường thẳng c có đi qua điểm M hay không (Hình 38a)?
- Nếu đường thẳng a song song với đường thẳng b thì đường thẳng a có song song với đường thẳng c hay không (Hình 38b)?
Phương pháp giải:
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy đồng quy hoặc đôi một song song với nhau.
Lời giải chi tiết:
- Nếu hai đường thẳng a và b cắt nhau tại điểm M thì đường thẳng c đi qua điểm M.
- Nếu đường thẳng a song song với đường thẳng b thì đường thẳng a song song với đường thẳng c.
LT-VD2
Trả lời câu hỏi Luyện tập - Vận dụng 2 trang 99 SGK Toán 11 Cánh diều
Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAD) và (SBC).
Phương pháp giải:
Để xác định giao tuyến của hai mặt phẳng, ta tìm điểm chung của chúng.
Đường thẳng đi qua hai điểm chung là giao tuyến.
Lời giải chi tiết:
Ta có: AB thuộc (SAB).
CD thuộc (SCD).
Mà AB // CD, S là giao điểm của hai mặt phẳng (SAB) và (SCD).
Từ S kẻ Sx sao cho Sx // AB // CD.
Vậy Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
Chứng minh tương tự, ta có: Sy là giao tuyến của hai mặt phẳng (SAD) và (SBC).
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 99 SGK Toán 11 Cánh diều
Trong mặt phẳng, hãy nêu vị trí tương đối của hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba.
Phương pháp giải:
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
Lời giải chi tiết:
Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
LT-VD3
Trả lời câu hỏi Luyện tập - Vận dụng 3 trang 100 SGK Toán 11 Cánh diều
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của các đoạn thẳng SA, SC. Lấy các điểm P, Q lần lượt thuộc các đoạn thẳng AB, BC sao cho \(\frac{{BP}}{{BA}} = \frac{{BQ}}{{BC}} = \frac{1}{3}\). Chứng minh rằng MN song song với PQ.
Phương pháp giải:
- Nếu ba mp phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc song song với nhau.
- Hệ quả: Nếu hai mp phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
- Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
\(\left\{ \begin{array}{l}a \ne b\\a//c\\b//c\end{array} \right. \Rightarrow a//b\)
Lời giải chi tiết:
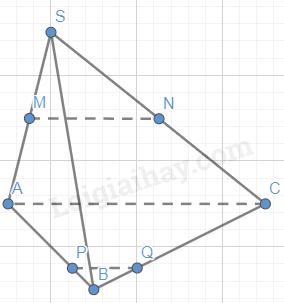
Ta có M, N lần lượt là trung điểm của SA, SC.
Do đó, tam giác SAC có MN // AC (1)
Ta có: \(\frac{{BP}}{{BA}} = \frac{{BQ}}{{BC}} = \frac{1}{3}\).
Suy ra: PQ // AC (2)
Từ (1) và (2), suy ra: MN // PQ.
Bình luận
Chia sẻ
- Bài 1 trang 100 SGK Toán 11 tập 1 - Cánh diều
- Bài 2 trang 100 SGK Toán 11 tập 1 - Cánh diều
- Bài 3 trang 100 SGK Toán 11 tập 1 - Cánh diều
- Bài 4 trang 100 SGK Toán 11 tập 1 - Cánh diều
- Bài 5 trang 100 SGK Toán 11 tập 1 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
