Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Cánh diều
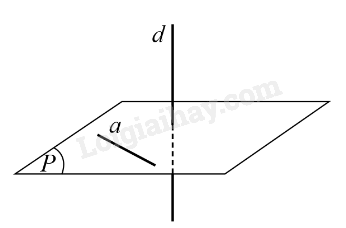
1. Định nghĩa Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P), kí hiệu (d bot left( P right)) hoặc (left( P right) bot d).
1. Định nghĩa
Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P), kí hiệu \(d \bot \left( P \right)\) hoặc \(\left( P \right) \bot d\).
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Nhận xét: Ta có thể chứng minh hai đường thẳng vuông góc bằng cách chứng minh một đường thẳng vuông góc với một mặt phẳng chứa đường thẳng kia.
3. Tính chất
- Tính chất 1: Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
- Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
- Tính chất 3:
Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
- Tính chất 4:
Cho hai mặt phẳng song song. Một đường thẳng vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
5. Phép chiếu vuông góc
Cho mặt phẳng (P) và một điểm M tuỳ ý trong không gian. Lấy đường thẳng d đi qua M và vuông góc với (P), gọi giao điểm của d và (P) là M’. Điểm M’ gọi là hình chiếu vuông góc (hay hình chiếu) của điểm M trên (P).
Cho mặt phẳng (P). Quy tắc đặt tương ứng mỗi điểm M trong không gian với hình chiếu vuông góc M’ của điểm đó lên mặt phẳng (P) được gọi là phép chiếu vuông góc lên mặt phẳng (P).
Nhận xét: Vì phép chiếu vuông góc là một trường hợp đặc biệt của phép chiếu song song (khi phương chiếu vuông góc với mặt phẳng chiếu) nên phép chiếu vuông góc có đầy đủ các tính chất của phép chiếu song song.
6. Định lí ba đường vuông góc
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng d nằm trong mặt phẳng (P). Khi đó, d vuông góc với a khi và chỉ khi d vuông góc với hình chiếu a’ của a trên (P).
Các bài khác cùng chuyên mục













Danh sách bình luận