Bài 2. Đường thẳng vuông góc với mặt phẳng Toán 11 Cánh..

Bài 3 trang 88 SGK Toán 11 tập 2 – Cánh Diều

Cho tứ diện ABCD có (AB bot (BCD)), các tam giác BCD và ACD là những tam giác nhọn.

Đề bài

Cho tứ diện ABCD có \(AB \bot (BCD)\), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng:

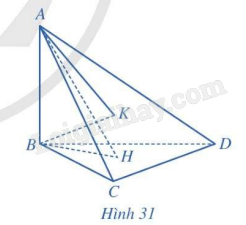
a) \(CD \bot (ABH)\)

b) \(CD \bot (ABK)\)

c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm

Phương pháp giải - Xem chi tiết

Dựa vào điều kiện đường thẳng vuông góc với mặt phẳng để chứng minh

Lời giải chi tiết

a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)

Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)

Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)

b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)

Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)

c) Ta có: \( CD \bot \left( {ABH} \right)\) và \(CD \bot \left( {ABK} \right)\). Mà theo tính chất 1, chỉ có duy nhất 1 mặt phẳng đi qua A và B vuông góc với CD. Nên \(\left( {ABH} \right) \equiv \left( {ABK} \right)\).

Ta có H là trực tâm của tam giác BCD nên BH giao với CD tại 1 điểm I, K là trực tâm của tam giác ACD nên AK giao với CD tại 1 điểm I'.

Mà (ABHK) cắt CD tại 1 điểm thuộc CD.

Nên I và I' trùng nhau hay AK, BH, CD cùng đi qua một điểm.

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 6 phiếu

Bài tiếp theo

Bài 4 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Cho tứ diện ABCD có (AB bot (BCD),BC bot CD). Gọi M và N lần lượt là hình chiếu vuông góc của B trên AC và AD. Chứng minh rằng:
Bài 5 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Cho hình chóp O.ABC có (widehat {AOB} = widehat {BOC} = widehat {COA} = 90^circ ). Chứng minh rằng:
Bài 2 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC).
Bài 1 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Quan sát Hình 30 (hai cột của biển báo, mặt đường)
Giải mục 6 trang 87 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P)
Giải mục 5 trang 85 SGK Toán 11 tập 2 - Cánh Diều
Trong mặt phẳng (P). Xét một điểm M tùy ý trong không gian.
Giải mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P).
Giải mục 3 trang 81, 82 SGK Toán 11 tập 2 - Cánh Diều
Cho điểm O và đường thẳng a.
Giải mục 2 trang 81 SGK Toán 11 tập 2 - Cánh Diều
Hình 12 mô tả cửa tròn xoay, ở đó trục cửa và hai mép cửa gợi nên hình ảnh các đường thẳng d
Giải mục 1 trang 80 SGK Toán 11 tập 2 - Cánh Diều
Hình 10 mô tả một người thợ xây đang thả dây dọi vuông góc với nền nhà.
Giải hoạt động mở đầu trang 80 SGK Toán 11 tập 2 – Cánh Diều
Trong Hình 9, cột gỗ thẳng đứng và sàn nhà nằm ngang gợi nên hình ảnh đường thẳng vuông góc với mặt phẳng.
Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Cánh diều
1. Định nghĩa Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P), kí hiệu \(d \bot \left( P \right)\) hoặc \(\left( P \right) \bot d\).