Lý thuyết Góc giữa đường thẳng và mặt phẳng, góc nhị diện - Toán 11 Cánh diều
1. Góc giữa đường thẳng và mặt phẳng Cho đường thẳng d và mặt phẳng (P), ta có định nghĩa sau:
1. Góc giữa đường thẳng và mặt phẳng
Cho đường thẳng d và mặt phẳng (P), ta có định nghĩa sau:
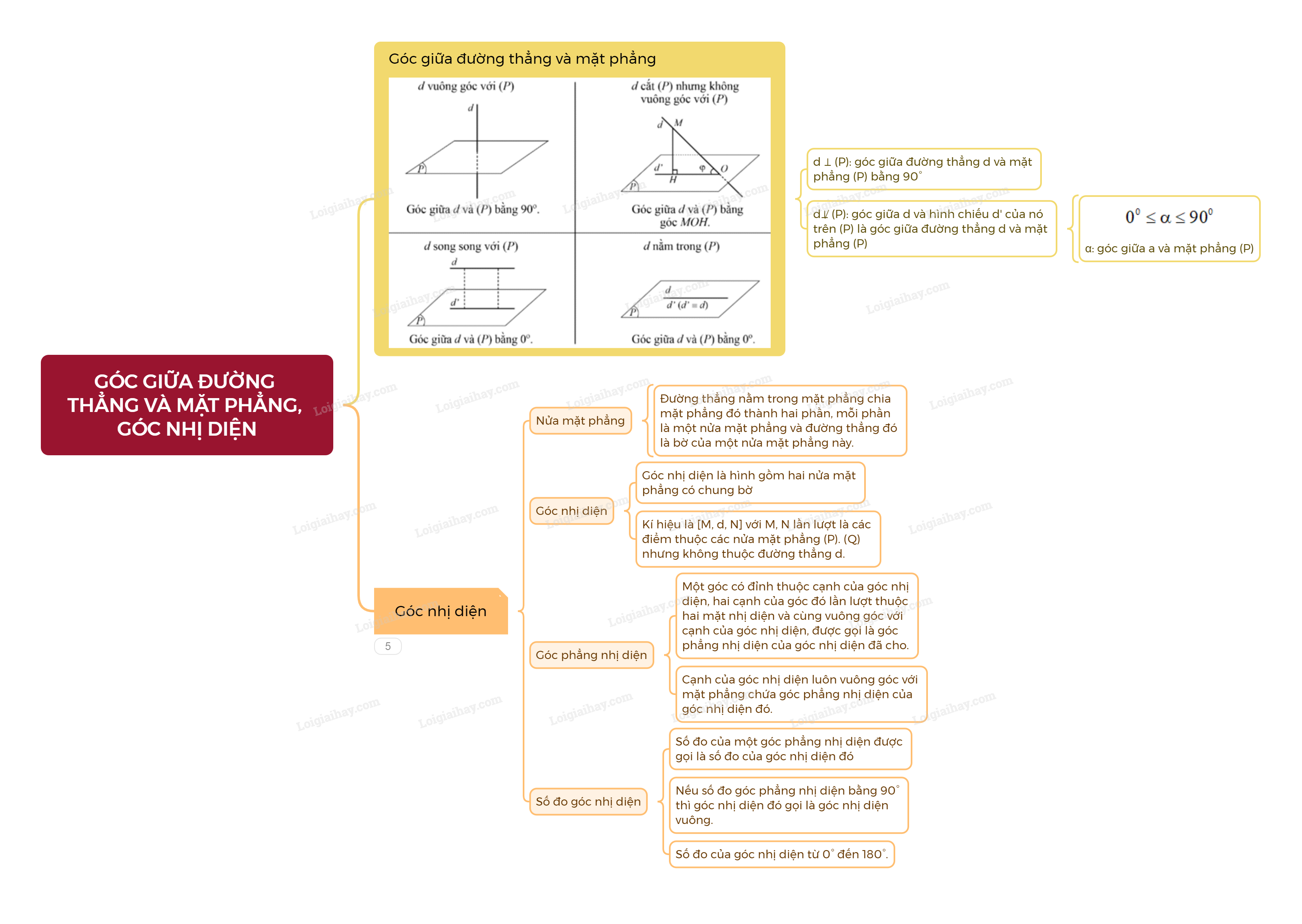
- Nếu đường thẳng d vuông góc với mặt phẳng (P) thì góc giữa d và (P) bằng \({90^0}\).
- Nếu đường thẳng d không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng d và mặt phẳng (P) là góc giữa d và hình chiếu d’ của đường thẳng d trên (P).

Nhận xét: Góc giữa đường thẳng và mặt phẳng có số đo từ \({0^0}\) đến \({90^0}\).
2. Góc nhị diện
a) Nửa mặt phẳng
Một đường thẳng nằm trong mặt phẳng chia mặt phẳng đó thành hai phần, mỗi phần được gọi là một nửa mặt phẳng và đường thẳng đó được gọi là bờ của một nửa mặt phẳng này.
b) Góc nhị diện
Góc nhị diện là hình gồm hai nửa mặt phẳng có chung bờ.
Ví dụ: Xét góc nhị diện gồm hai nửa mặt phẳng (P) và (Q) có chung bờ là đường thẳng d, kí hiệu là [P, d, Q]. Đường thẳng d gọi là cạnh của góc nhị diện, mỗi nửa mặt phẳng (P) và (Q) gọi là một mặt của góc nhị diện.
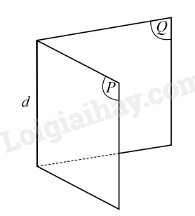
Chú ý: Góc nhị diện còn được kí hiệu là [M, d, N] với M, N lần lượt là các điểm thuộc các nửa mặt phẳng (P), (Q) nhưng không thuộc đường thẳng d.
c) Góc phẳng nhị diện
Trong không gian, cho góc nhị diện. Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó lần lượt thuộc hai mặt nhị diện và cùng vuông góc với cạnh của góc nhị diện, được gọi là góc phẳng nhị diện của góc nhị diện đã cho.
Ví dụ: Cho góc nhị diện [P, d, Q]. Lấy O thuộc d, hai tia Ox, Oy lần lượt nằm trên hai nửa mặt phẳng (P), (Q) và cùng vuông góc với d. Khi đó góc xOy là góc phẳng nhị diện của góc nhị diện [P, d, Q].
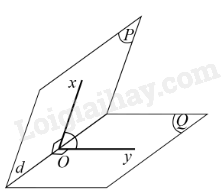
Nhận xét: Cạnh của góc nhị diện luôn vuông góc với mặt phẳng chứa góc phẳng nhị diện của góc nhị diện đó.
d) Số đo của góc nhị diện
- Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.
- Nếu số đo góc phẳng nhị diện bằng 90° thì góc nhị diện đó gọi là góc nhị diện vuông.
Nhận xét: Số đo của góc nhị diện từ \({0^0}\) đến \({180^0}\).
3. Bài tập về góc nhị diện
Bài 1. Cho tứ diện \(ABCD\) có cạnh $AB$, $BC$, $CD$ bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
A. Góc giữa \(AC\) và \(\left( {BCD} \right)\) là góc \(ACB\).
B. Góc giữa \(AD\) và \(\left( {ABC} \right)\) là góc \(ADB\).
C. Góc giữa \(AC\) và \(\left( {ABD} \right)\) là góc \(CAB\).
D. Góc giữa \(CD\) và \(\left( {ABD} \right)\) là góc \(CBD\).
Lời giải:
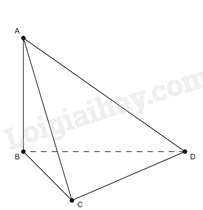
Từ giả thiết ta có \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot CD\end{array} \right. \Rightarrow AB \bot \left( {BCD} \right)\).
Do đó \(\left( {AC,\left( {BCD} \right)} \right) = \left( {AC,BC} \right) = \widehat {ACB}\).
Chọn đáp án A.
Bài 2. Cho tam giác \(ABC\) vuông cân tại \(A\) và \(BC = a.\) Trên đường thẳng qua \(A\) vuông góc với \(\left( {ABC} \right)\) lấy điểm \(S\) sao cho $SA = \dfrac{{a\sqrt 6 }}{2}$. Tính số đo góc giữa đường thẳng \(SA\) và \(\left( {ABC} \right)\)
A. \(30^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(90^\circ \).
Lời giải: \(SA \bot \left( {ABC} \right) \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = 90^\circ \).
Chọn đáp án D.
Bài 3. Cho hình lập phương\(ABCD.A'B'C'D'\). Gọi $\alpha $ là góc giữa $AC'$ và mp $\left( {A'BCD'} \right).$ Chọn khẳng định đúng trong các khẳng định sau?
A. $\alpha {\rm{ }} = {\rm{ }}{30^0}.$
B. \(\tan \alpha = \dfrac{2}{{\sqrt 3 }}.\)
C. $\alpha {\rm{ }} = {\rm{ }}{45^0}.$
D. \(\tan \alpha = \sqrt 2 .\)
Lời giải:
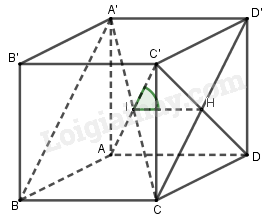
Gọi $\left\{ \begin{array}{l}A'C \cap AC' = I\\C'D \cap CD' = H\end{array} \right.$
mà \(\left\{ \begin{array}{l}C'D \bot CD'\\C'D \bot A'D'\end{array} \right. \Rightarrow C'D \bot \left( {A'BCD'} \right) \Rightarrow IH\) là hình chiếu vuông góc của \(IC'\) lên \(\left( {A'BCD'} \right) \Rightarrow \widehat {C'IH}\)là góc giữa \(IC'\) và \(\left( {A'BCD'} \right)\) và cũng là góc giữa \(AC'\) và \(\left( {A'BCD'} \right).\) Mà \(\tan \widehat {C'IH} = \dfrac{{C'H}}{{IH}} = \dfrac{1}{{\sqrt 2 }}.2 = \sqrt 2 .\)
Chọn đáp án D.
Bài 4. Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho
B. Nếu \(a\) và \(b\) song song (hoặc \(a\) trùng với \(b\)) thì góc giữa đường thẳng $a$ và mặt phẳng \(\left( P \right)\) bằng góc giữa đường thẳng \(b\) và mặt phẳng \(\left( P \right)\) .
C. Nếu góc giữa đường thẳng $a$ và mặt phẳng \(\left( P \right)\) bằng góc giữa đường thẳng \(a\) và mặt phẳng \(\left( Q \right)\) thì mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( Q \right)\).
D. Góc giữa đường thẳng $a$ và mặt phẳng \(\left( P \right)\) bằng góc giữa đường thẳng \(b\) và mặt phẳng \(\left( P \right)\) thì \(a\) song song với \(b\).
Lời giải: Đáp án A sai vì nếu trường hợp đường thẳng vuông góc với mặt phẳng thì định nghĩa đó không còn đúng.
Đáp án C sai vì \(\left( P \right)\) và \(\left( Q \right)\) có thể trùng nhau.
Đáp án D sai vì \(a,b\) có thể trùng nhau.
Chọn đáp án B.
Bài 5. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và \(SA = SB = SC = b\). Gọi \(G\) là trọng tâm \(\Delta ABC\). Độ dài \(SG\) là:
A. $\dfrac{{\sqrt {9{b^2} + 3{a^2}} }}{3}$.
B. $\dfrac{{\sqrt {{b^2} - 3{a^2}} }}{3}$.
C. $\dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}$.
D. $\dfrac{{\sqrt {{b^2} + 3{a^2}} }}{3}$.
Lời giải:
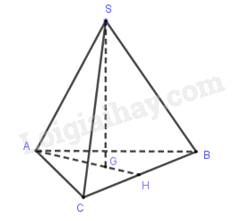
Theo bài ra hình chóp \(S.ABC\) là hình chóp tam giác đều.
Gọi \(H\) là trung điểm của \(BC\), ta có \(SG \bot (ABC),G \in AH\).
Mà \(AH = \dfrac{{a\sqrt 3 }}{2} \Rightarrow AG = \dfrac{2}{3}AH = \dfrac{{a\sqrt 3 }}{3}\).
Tam giác \(SAG\) vuông tại \(G\) nên theo định lý Pi-ta-go ta có :
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - \dfrac{{{a^2}}}{3}} = \sqrt {\dfrac{{3{b^2} - {a^2}}}{3}} = \dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}\)
Chọn đáp án C.
Bài 6. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông. Mặt bên \(SAB\) là tam giác đều có đường cao \(SH\) vuông góc với \(mp(ABCD)\). Gọi \(\alpha \) là góc giữa \(BD\) và \(mp(SAD)\). Chọn khẳng định đúng trong các khẳng định sau?
A. \(\alpha = {60^0}\).
B. \(\alpha = {30^0}\).
C. \(\cos \alpha = \dfrac{{\sqrt 3 }}{{2\sqrt 2 }}\).
D. \(\sin \alpha = \dfrac{{\sqrt 3 }}{{2\sqrt 2 }}\).
Lời giải:
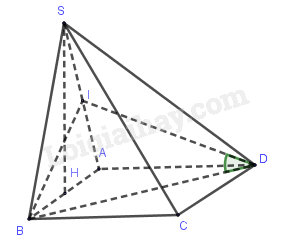
Gọi \(I\) là trung điểm ${\rm{AS}} \Rightarrow {\rm{BI}} \bot {\rm{SA}}$
Ta có: \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot AD\)
Mà \(AD \bot AB\) nên \(AD \bot \left( {SAB} \right) \Rightarrow AD \bot BI\)
Suy ra \(BI \bot (SAD) \Rightarrow \alpha = \widehat {IDB}\)
Ta có: \(BI = \dfrac{{AB\sqrt 3 }}{2},BD = AB\sqrt 2 \Rightarrow \sin \alpha = \dfrac{{BI}}{{BD}} = \dfrac{{\sqrt 3 }}{{2\sqrt 2 }}\)
Chọn đáp án D.
Bài 7. Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cạnh huyền $BC = a$. Hình chiếu vuông góc của \(S\) lên $\left( {ABC} \right)$ trùng với trung điểm$BC$. Biết $SB = a$. Tính số đo của góc giữa $SA$ và $\left( {ABC} \right)$.
A.\(30^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(75^\circ \).
Lời giải:
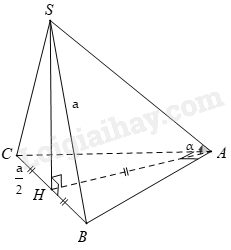
Gọi \(H\) là trung điểm của \(BC\) suy ra
\(AH = BH = CH = \dfrac{1}{2}BC = \dfrac{a}{2}\).
Ta có: \(SH \bot \left( {ABC} \right) \Rightarrow SH = \sqrt {S{B^2} - B{H^2}} = \dfrac{{a\sqrt 3 }}{2}\)
\(\widehat {\left( {SA,\left( {ABC} \right)} \right)} = \widehat {\left( {SA,HA} \right)} = \widehat {SAH} = \alpha \)
$ \Rightarrow \tan \alpha = \dfrac{{SH}}{{AH}} = \sqrt 3 \Rightarrow \alpha = 60^\circ $.
Chọn đáp án C.
Các bài khác cùng chuyên mục













Danh sách bình luận