Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh -..
Bài 30 trang 120 SGK Toán 7 tập 1
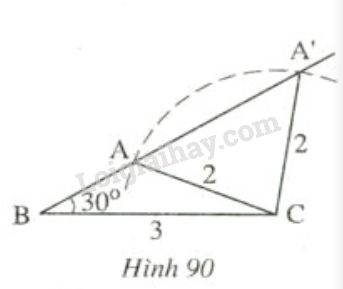
Trên hình 90, các tam giác ABC và A'BC có cạnh chung BC= 3cm cạnh chung BC = 3cm, CA=CA'= 2cm,
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
Trên hình 90, các tam giác \(ABC\) và \(A'BC\) có cạnh chung \(BC= 3cm\), \(CA=CA'= 2cm\), \(\widehat{ABC }=\widehat{A'BC }= 30^o\) nhưng hai tam giác đó không bằng nhau.
Tại sao ở đây không áp dụng trường hợp cạnh góc cạnh để kết luận \(∆ABC=∆A'BC?\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
\(\widehat {ABC}\) không phải là góc xen giữa hai cạnh \(BC\) và \(CA\), \(\widehat {A'BC}\) không phải là góc xen giữa hai cạnh \(BC\) và \(CA'\).
Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận \(∆ABC=∆A'B C.\)
(bởi vì để có 2 tam giác bằng nhau theo trường hợp cạnh góc cạnh thì góc bắt buộc phải xen giữa hai cạnh bằng nhau tương ứng đó)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 31 trang 120 SGK Toán 7 tập 1
- Bài 32 trang 120 SGK Toán 7 tập 1
- Đề kiểm tra 15 phút - Đề số 1 - Bài 2,3,4,5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 2,3,4,5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 2,3,4,5 - Chương 2 - Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
