-
Toán 11 tập 1 - Kết nối tri thức với cuộc sống
-
Giải Toán 11 tập 2 - Kết nối tri thức với cuộc sống
Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
Bài 21. Phương trình, bất phương trình mũ và lôgarit To..
Lý thuyết Phương trình, bất phương trình mũ và lôgarit - Toán 11 Kết nối tri thức
1. Phương trình mũ
Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh
1. Phương trình mũ
Phương trình mũ cơ bản có dạng \({a^x} = b\)(với \(0 < a \ne 1\)).
- Nếu b > 0 thì phương trình có nghiệm duy nhất \(x = {\log _a}b\).
- Nếu b \( \le \) 0 thì phương trình vô nghiệm.
Minh họa bằng đồ thị:
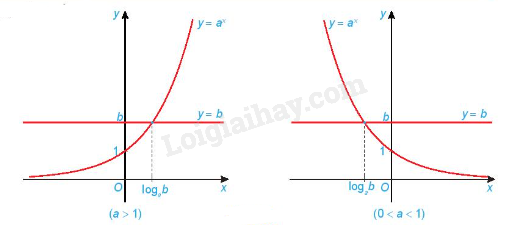
Chú ý: Phương pháp giải phương trình mũ bằng cách đưa về cùng cơ số:
Nếu \(0 < a \ne 1\) thì \({a^u} = {a^v} \Leftrightarrow u = v\).
2. Phương trình lôgarit
Phương trình lôgarit cơ bản có dạng \({\log _a}x = b\left( {0 < a \ne 1} \right)\).
Phương trình lôgarit cơ bản \({\log _a}x = b\) có nghiệm duy nhất \(x = {a^b}\).
Minh họa bằng đồ thị:
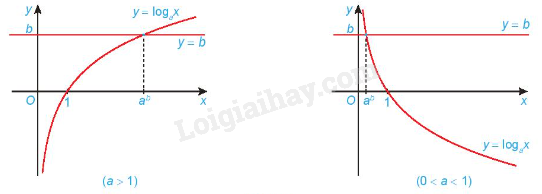
Chú ý: Phương pháp giải phương trình lôgarit bằng cách đưa về cùng cơ số:
Nếu \(u,v > 0\) và \(0 < a \ne 1\) thì \({\log _a}u = {\log _a}v \Leftrightarrow u = v\).
3. Bất phương trình mũ
Bất phương trình mũ cơ bản có dạng \({a^x} > b\) (hoặc \({a^x} \ge b,{a^x} < b,{a^x} \le b\)) với \(a > 0,a \ne 1\).
Xét bất phương trình dạng \({a^x} > b\):
- Nếu \(b \le 0\) thì tập nghiệm của bất phương trình là \(\mathbb{R}\).
- Nếu b > 0 thì bất phương trình tương đương với \({a^x} > {a^{{{\log }_a}b}}\).
Với a > 1, nghiệm của bất phương trình là \(x > {\log _a}b\).
Với \(0 < a < 1\), nghiệm của bất phương trình là \(x < {\log _a}b\).
Chú ý:
a) Các bất phương trình mũ cơ bản còn lại được giải tương tự.
b) Nếu a > 1 thì \({a^u} > {a^v} \Leftrightarrow u > v\).
Nếu 0 < a < 1 thì \({a^u} > {a^v} \Leftrightarrow u < v\).
4. Bất phương trình lôgarit
Bất phương trình lôgarit cơ bản có dạng \({\log _a}x > b\)(hoặc \({\log _a}x \ge b,{\log _a}x < b,{\log _a}x \le b\)) với \(a > 0,a \ne 1\).
Xét bất phương trình dạng \({\log _a}x > b\):
- Nếu a > 1 thì nghiệm của bất phương trình là \(x > {a^b}\).
- Nếu 0 < a < 1 thì nghiệm của bất phương trình là \(0 < x < {a^b}\).
Chú ý:
a) Các bất phương trình lôgarit cơ bản còn lại được giải tương tự.
b) Nếu a > 1 thì \({\log _a}u > {\log _a}v \Leftrightarrow u > v > 0\).
Nếu 0 < a < 1 thì \({\log _a}u > {\log _a}v \Leftrightarrow 0 < u < v\).
Bình luận
Chia sẻ
- Giải mục 1 trang 20, 21 SGK Toán 11 tập 2 - Kết nối tri thức
- Giải mục 2 trang 21, 22 SGK Toán 11 tập 2 - Kết nối tri thức
- Giải mục 3 trang 22, 23 SGK Toán 11 tập 2 - Kết nối tri thức
- Giải mục 4 trang 23, 24 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 6.20 trang 24 SGK Toán 11 tập 2 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Đạo hàm cấp hai - Toán 11 Kết nối tri thức
- Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Kết nối tri thức
- Lý thuyết Định nghĩa và ý nghĩa của đạo hàm - Toán 11 Kết nối tri thức
- Lý thuyết Công thức nhân xác suất cho hai biến cố độc lập - Toán 11 Kết nối tri thức
- Lý thuyết Công thức cộng xác suất - Toán 11 Kết nối tri thức
- Lý thuyết Đạo hàm cấp hai - Toán 11 Kết nối tri thức
- Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Kết nối tri thức
- Lý thuyết Định nghĩa và ý nghĩa của đạo hàm - Toán 11 Kết nối tri thức
- Lý thuyết Công thức nhân xác suất cho hai biến cố độc lập - Toán 11 Kết nối tri thức
- Lý thuyết Công thức cộng xác suất - Toán 11 Kết nối tri thức
