 Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
 Bài 16. Giới hạn của hàm số Toán 11 kết nối tri thức
Bài 16. Giới hạn của hàm số Toán 11 kết nối tri thức
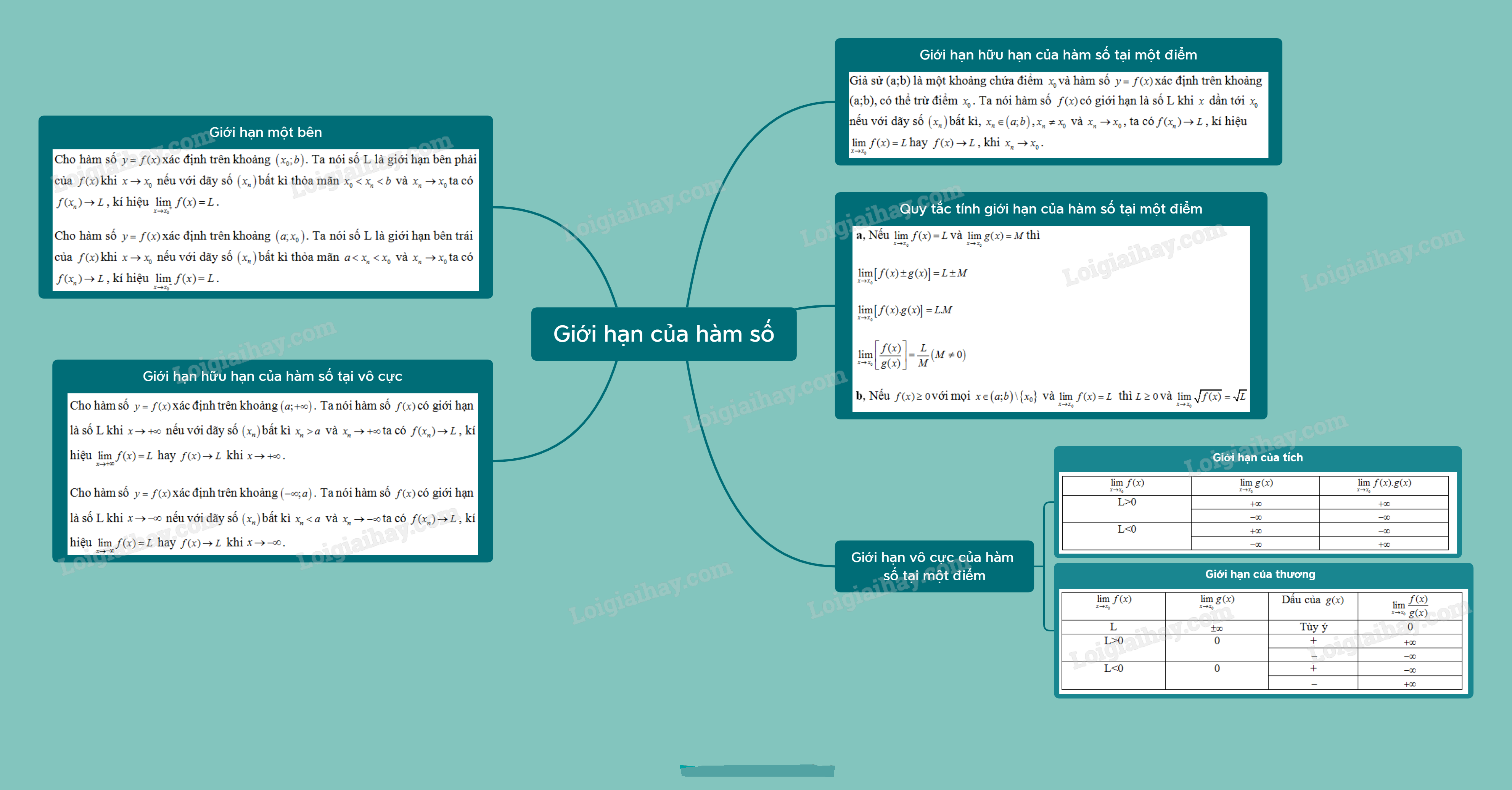
Lý thuyết Giới hạn của hàm số - SGK Toán 11 Kết nối tri thức
1. Giới hạn hữu hạn của hàm số tại một điểm
1. Giới hạn hữu hạn của hàm số tại một điểm
Giả sử (a;b) là một khoảng chứa điểm \({x_0}\)và hàm số \(y = f(x)\) xác định trên khoảng (a;b), có thể trừ điểm \({x_0}\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} \in \left( {a;b} \right)\),\({x_n} \ne {x_0}\) và \({x_n} \to {x_0}\), ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) hay \(f(x) \to L\), khi \({x_n} \to {x_0}\).
*Quy tắc tính giới hạn của hàm số tại một điểm
a) Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g(x) = M\) thì
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)\)
b) Nếu \(f(x) \ge 0\) với mọi \(x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) thì \(L \ge 0\) và \(\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)} = \sqrt L \).
* Giới hạn một bên
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {{x_0};b} \right)\). Ta nói số L là giới hạn bên phải của \(f(x)\) khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì thỏa mãn \({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\), ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\).
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;{x_0}} \right)\). Ta nói số L là giới hạn bên trái của khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì thỏa mãn \(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\), ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L\).
2. Giới hạn hữu hạn của hàm số tại vô cực
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x \to + \infty \) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} > a\) và \({x_n} \to + \infty \) ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to + \infty \).
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( { - \infty ;b} \right)\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x \to - \infty \) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} < b\) và \({x_n} \to - \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to - \infty \).
* Nhận xét:
Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
Với c là hằng số, \(\mathop {\lim }\limits_{x \to + \infty } c = c\), \(\mathop {\lim }\limits_{x \to - \infty } c = c\).
Với k là một số nguyên dương, ta có: \(\mathop {\lim }\limits_{x \to + \infty } (\frac{1}{{{x^k}}}) = 0,\mathop {\lim }\limits_{x \to - \infty } (\frac{1}{{{x^k}}}) = 0\).
3. Giới hạn vô cực của hàm số tại một điểm
a) Giới hạn vô cực
- Giả sử khoảng (a;b) chứa \({x_0}\) và hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\). Ta nói hàm số \(f(x)\) có giới hạn là \( + \infty \) khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \(\left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \({x_n} \to {x_0}\), ta có\(f({x_n}) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = + \infty \).
Ta nói hàm số \(f(x)\) có giới hạn \( - \infty \) khi \(x \to {x_0}\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = - \infty \), nếu \(\mathop {\lim }\limits_{x \to {x_0}} \left[ { - f(x)} \right] = + \infty \).
- Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {{x_0};b} \right)\). Ta nói hàm số \(f(x)\) có giới hạn \( + \infty \) khi \(x \to {x_0}\) về bên phải nếu với dãy số \(\left( {{x_n}} \right)\) bất kì thỏa mãn \({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\) ta có \(f({x_n}) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \).
Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {a;{x_0}} \right)\). Ta nói hàm số \(f(x)\)có giới hạn \( + \infty \) khi \(x \to {x_0}\) về bên trái nếu với dãy số \(\left( {{x_n}} \right)\)bất kì thỏa mãn \(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \).
Các giới hạn một bên\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \), \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \) được định nghĩa tương tự.
b) Một số quy tắc tính giới hạn vô cực
*Giới hạn của tích\(\mathop {\lim }\limits_{x \to {x_0}} f(x).g(x)\)

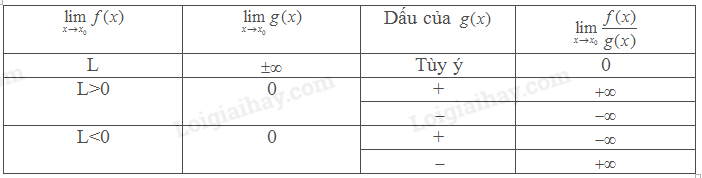
*Giới hạn của thương \(\frac{{f(x)}}{{g(x)}}\)
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải mục 1 trang 111, 112, 113 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải mục 2 trang 114, 115 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải mục 3 trang 115, 116, 117, 118 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 5.7 trang 118 SGK Toán 11 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức












Danh sách bình luận