Giải bài 6 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo

Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước).

Đề bài

Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước). Chiếc cầu trong Hình 1 có bộ phận chống đỡ dạng parabol. Một người muốn thực hiện một cú nhày bungee từ giữa cầu xuống với dây an toàn. Người này cần trang bị sợi dây an toàn dài bao nhiêu mét? Biết rằng chiều dài của sợi dây đó bằng một phần ba khoảng cách từ vị trí bắt đầu nhảy đến mặt nước.

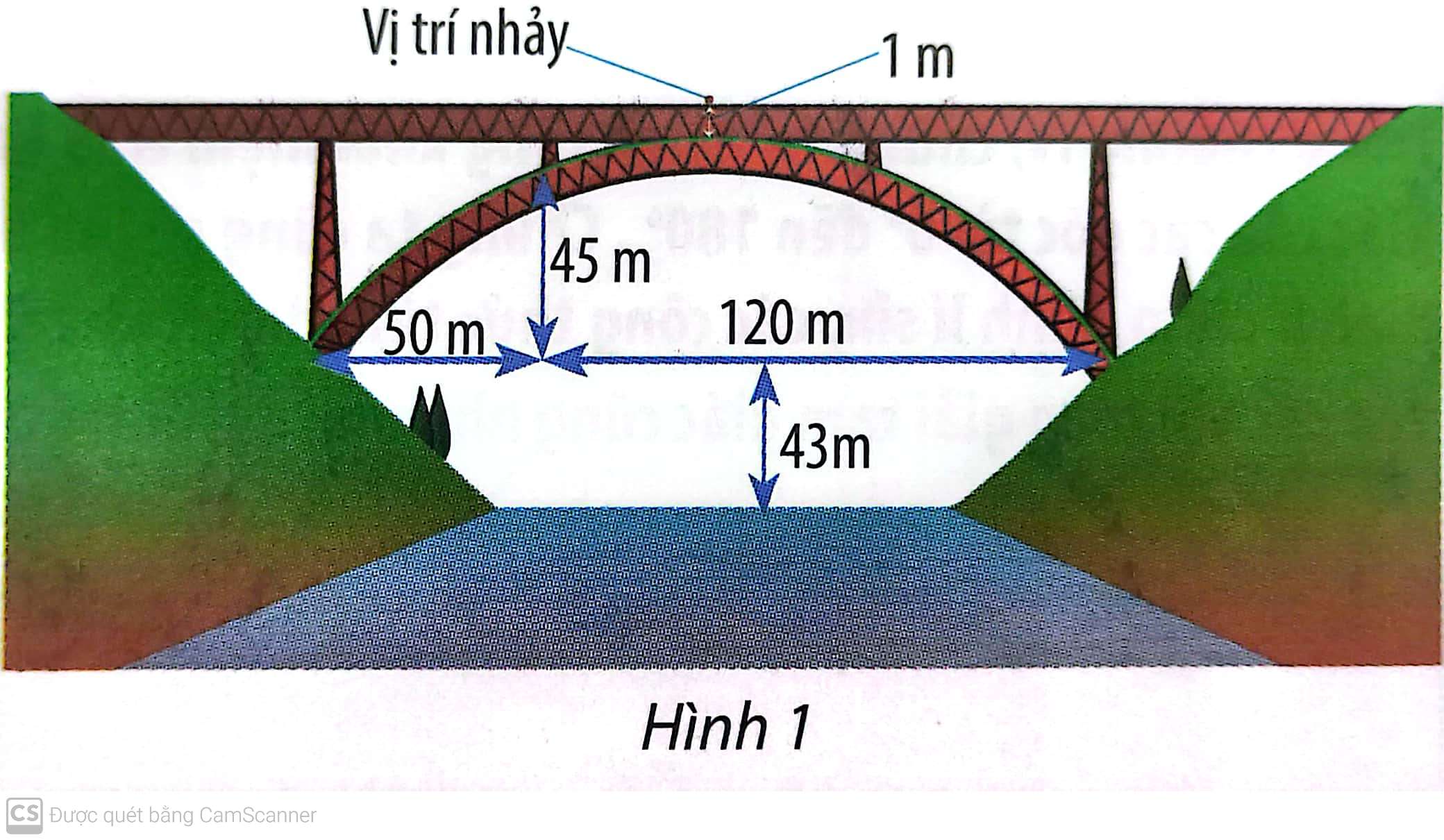
Phương pháp giải - Xem chi tiết

Gắn hệ trục tọa độ, gọi công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.

Xác định hàm số và xác định tung độ của đỉnh.

Lời giải chi tiết

Gọi \(y = f(x) = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.

Chọn hệ trục tọa độ Oxy như hình dưới:

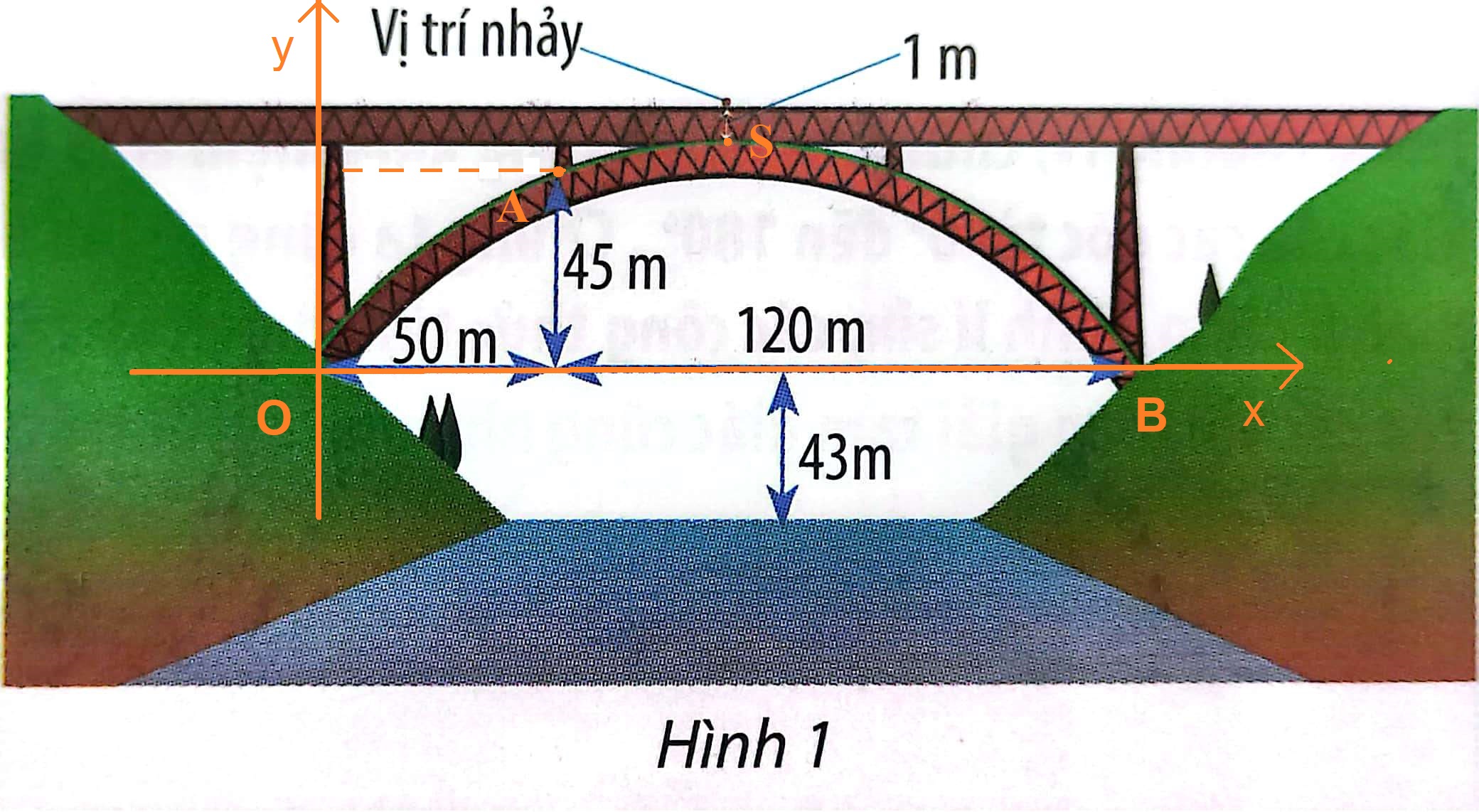
Gọi S là đỉnh của parabol, dưới vị trí nhảy 1m.

A, B là các điểm như hình vẽ.

Dễ thấy: A (50; 45) và B (120+50; 0) = (170; 0).

Các điểm O, A, B đều thuộc đồ thị hàm số.

Do đó:

\(f(0) = a{.0^2} + b.0 + c = 0 \Leftrightarrow c = 0\)

\(f(50) = a{.50^2} + b.50 + c = 45 \Leftrightarrow a{.50^2} + b.50 = 45\)

\(f(170) = a{.170^2} + b.170 + c = 0 \Leftrightarrow a{.170^2} + b.170 = 0 \Leftrightarrow a.170+ b = 0\)

Giải hệ phương trình \(\left\{ \begin{array}{l}a{.50^2} + b.50 = 45\\a.170 + b = 0\end{array} \right.\) ta được \(a = - \frac{{3}}{{400}};b = \frac{{51}}{{40}}\)

Vậy \(y = f(x) = - \frac{{3}}{{400}}{x^2} + \frac{{51}}{{40}}x\)

Đỉnh S có tọa độ là \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - \frac{{51}}{{40}}}}{{2.\left( { - \frac{{3}}{{400}}} \right)}} = 85;\;{y_S} = - \frac{{3}}{{400}}.8{5^2} + \frac{{51}}{{40}}.85 = \frac{{867}}{{16}} \approx 54,2\)

Khoảng cách từ vị trí bắt đầu nhảy đến mặt nước là: \(1 + 54,2 + 43 = 98,2(m)\)

Vậy chiều dài của sợi dây đó là: \(98,2:3 \approx 32,7\,(m)\)

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 8 phiếu

Bài tiếp theo

Giải bài 7 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80 m, lúc đó máy bay đang bay với vận tốc 50 m/s. Để thùng hàng cứu trợ rơi đúngvị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí nào? Biết rằng nếu chọn gốc toạ độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì toạ độ của hàng cứu trợ được cho bởi hệ sau:
Giải bài 5 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Biết rằng hàm số giảm trên khoảng tăng trên khoảng và có tập giá trị là. Xác định giá trị của m và n.
Giải bài 4 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30 km/h. a) Hãy biểu thị quãng đường s (tính bằng kilômét) mà người này đi được sau t phút bằng một hàm số. b) Vẽ đồ thị biểu diễn hàm số s theo t.
Giải bài 3 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Vẽ đồ thị các hàm số sau:
Giải bài 2 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai:
Giải bài 1 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm tập xác định của các hàm số sau: