Giải bài 4 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo

Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30 km/h. a) Hãy biểu thị quãng đường s (tính bằng kilômét) mà người này đi được sau t phút bằng một hàm số. b) Vẽ đồ thị biểu diễn hàm số s theo t.

Đề bài

Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42 km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30 km/h.

a) Hãy biểu thị quãng đường s (tính bằng kilômét) mà người này đi được sau t phút bằng một hàm số.

b) Vẽ đồ thị biểu diễn hàm số s theo t.

Lời giải chi tiết

a) Đổi: 1 giờ 30 phút = 1,5 giờ; 15 phút = 0,25 giờ; t phút = \(\frac{t}{{60}}\) giờ.

Với \(t \le 90\) (phút), quãng đường s mà người đó đi được là: \(42.\frac{t}{{60}} = 0,7t\) (km).

Sau khi đi được 0,7.90 = 63 km thì người này nghỉ trong khoảng thời gian 15 phút nên khoảng thời gian từ 90 phút đến 105 phút người này giữ quãng đường không đổi là 63 km. Do đó s(t) = 63.

Với \(105 < t \le 105 + 120 = 225\) (phút), quãng đường s mà người đó đi được là: \(63 + (\frac{t}{{60}} - 1,5 - 0,25).30 = 0,5t + 10,5\) (km).

Như vậy hàm số tính quãng đường s (km) sau t phút là:

\(s = \left\{ \begin{array}{l}0,7t\quad \quad \quad \quad (0 \le t \le 90)\\63\quad \quad \quad \quad \;\;\;(90 < t \le 105)\\0,5t + 10,5\quad \;\;(105 < t \le 225)\end{array} \right.\)

Với \(0 \le t \le 90\) thì \(s = 0,7t\).

Trên đoạn [0;90] ta vẽ đường thẳng \(s = 0,7t\).

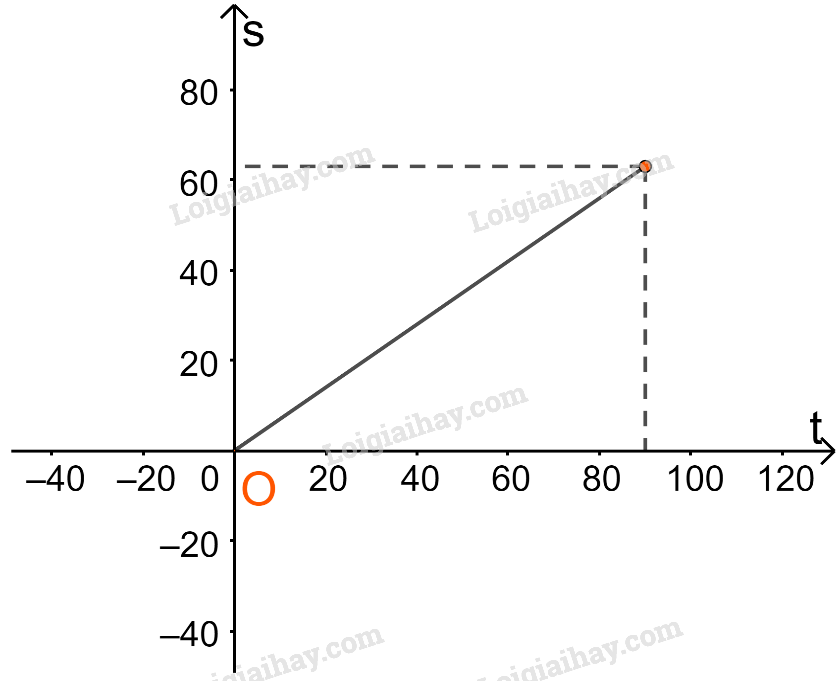
Với \(90 < t \le 105\) thì \(s = 63(km)\).

Trên nửa khoảng (90;105] ta vẽ đường thẳng \(s = 63\).

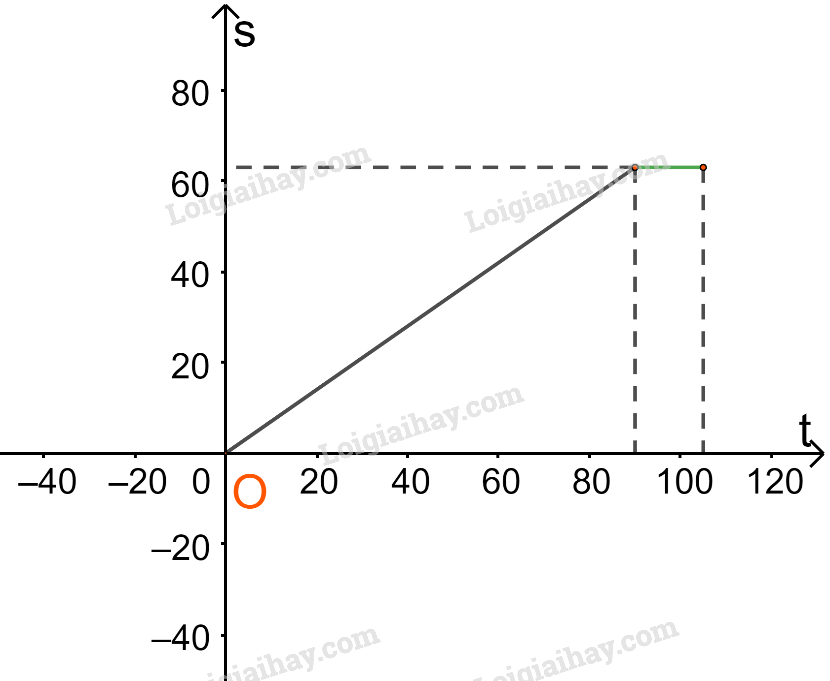
Với \(105 < t \le 225\)(phút) thì \(s = 0,5t + 10,5\) (km).

Trên nửa khoảng (105;225] ta vẽ đường thẳng \(s = 0,5t + 10,5\).

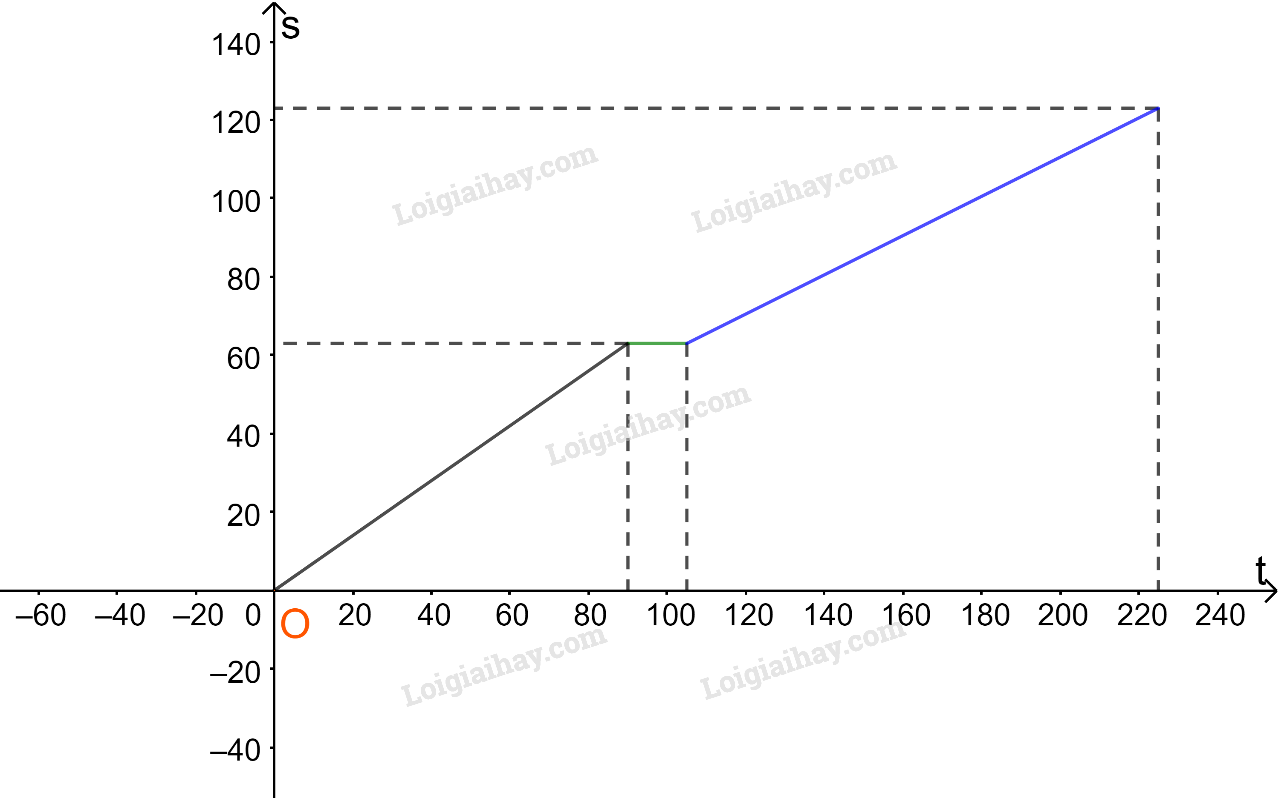
Như vậy ta được đồ thị biểu diễn hàm số s theo t như hình trên.

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 11 phiếu

Bài tiếp theo

Giải bài 5 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Biết rằng hàm số giảm trên khoảng tăng trên khoảng và có tập giá trị là. Xác định giá trị của m và n.
Giải bài 6 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước).
Giải bài 7 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80 m, lúc đó máy bay đang bay với vận tốc 50 m/s. Để thùng hàng cứu trợ rơi đúngvị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí nào? Biết rằng nếu chọn gốc toạ độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì toạ độ của hàng cứu trợ được cho bởi hệ sau:
Giải bài 3 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Vẽ đồ thị các hàm số sau:
Giải bài 2 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai:
Giải bài 1 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm tập xác định của các hàm số sau: