Giải Bài 5 trang 68 sách bài tập toán 7 - Cánh diều

Cho tam giác ABC có Tia phân giác của góc C cắt cạnh AB tại M. Tính số đo của \(\widehat {AMC}\) và \(\widehat {BMC}\)

Tổng hợp đề thi giữa kì 2 lớp 7 tất cả các môn - Cánh diều

Toán - Văn - Anh - KHTN...

Đề bài

Cho tam giác ABC có Tia phân giác của góc C cắt cạnh AB tại M. Tính số đo của \(\widehat {AMC}\) và \(\widehat {BMC}\)

Phương pháp giải - Xem chi tiết

- Tính góc C

- Vì CM là tia phân giác của góc C nên \(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat C}}{2}\)

- Tính số đo góc \(\widehat {AMC}\) và \(\widehat {BMC}\) dựa vào tổng ba góc trong một tam giác bằng \({180^o}\)

Lời giải chi tiết

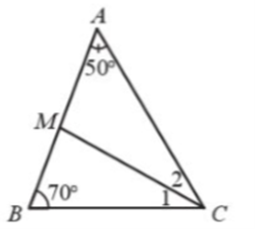
Xét ∆ABC có: \(\widehat {{A^{}}} + \widehat B + \widehat C = {180^o}\) (định lí tổng ba góc của một tam giác).

Suy ra \(\widehat {ACB} = {180^o} - \widehat {{A^{}}} - \widehat B = {180^o} - {50^o} - {70^o} = {60^o}\)

Vì tia CM là tia phân giác của nên ta có:

\(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat C}}{2} = \frac{{{{60}^o}}}{2} = {30^o}\)

Xét ∆AMC có: \(\widehat {AMC} + \widehat {{C_2}} + \widehat {{A^{}}} = {180^o}\) (tổng ba góc của một tam giác).

Suy ra \(\widehat {AMC} = {180^o} - \widehat {{C_2}} - \widehat {{A^{}}} = {180^o} - {30^o} - {50^o} = {100^o}\)

Xét ∆BMC có: \(\widehat {BMC} + \widehat {{C_1}} + \widehat B = {180^o}\) (tổng ba góc của một tam giác).

Suy ra \(\widehat {BMC} = {180^o} - \widehat {{C_1}} - \widehat B = {180^o} - {30^o} - {70^o} = {80^o}\)

Vậy \(\widehat {AMC} = {100^o};\widehat {BMC} = {80^o}\)

Bình luận

Chia sẻ

Bình chọn:

4 trên 3 phiếu

Bài tiếp theo

Giải Bài 6 trang 68 sách bài tập toán 7 - Cánh diều
Tính số đo các góc của tam giác ABC trong mỗi trường hợp sau: a) (widehat {{A^{}}} = widehat B = widehat C) ;
Giải Bài 7 trang 68 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H, AD là tia phân giác của \(\widehat {HAC}\) (hình 4)
Giải Bài 8 trang 69 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC. Kẻ HB vuông góc với AC tại H. Kẻ CK vuông góc với AB tại K, BH cắt CK tại I (Hình 5). Nếu \(\widehat {{A^{}}} < {90^o}\) thì khi đó ta có:
Giải Bài 9 trang 69 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC, tia phân giác của \(\widehat {BAC}\) cắt cạnh BC tại D. Tính số đo mỗi góc của tam giác ABC, biết \(\widehat {A{\rm{D}}B} = {80^o}\) và \(\widehat B = 1,5\widehat C\).
Giải Bài 10 trang 69 sách bài tập toán 7 - Cánh diều
Ở Hình 6 có \(\hat A = \hat B = 60^\circ \) và Cx là tia phân giác của góc ACy. Chứng minh Cx song song với AB.
Giải Bài 11 trang 69 sách bài tập toán 7 - Cánh diều
Ở Hình 7 có \(\widehat {BAD} = \widehat {BCD} = 90^\circ ,\widehat {ADB} = 15^\circ \) AD song song với BC. Chứng minh AB song song với DC.
Giải Bài 4 trang 68 sách bài tập toán 7 - Cánh diều
Bạn Bình phát biểu: “Không có tam giác ABC nào mà
Giải Bài 3 trang 68 sách bài tập toán 7 - Cánh diều
a) Cho biết một góc nhọn của tam giác vuông bằng \({40^o}\). Tính số đo góc nhọn còn lại.
Giải Bài 2 trang 68 sách bài tập toán 7 - Cánh diều
Quan sát hình 3:
Giải Bài 1 trang 68 sách bài tập toán 7 - Cánh diều
Cho tam giác MHK vuông tại H. ta có: