Giải bài 2 trang 82 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C.

Đề bài

Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C.

Phương pháp giải - Xem chi tiết

- Ta chứng minh I là giao của 3 đường phân giác trong tam giác ABC

- Từ đó ta chứng minh CI là phân giác góc C

Lời giải chi tiết

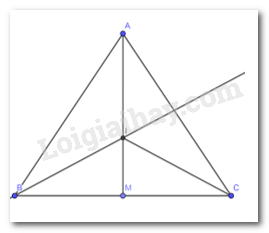
Xét tam giác ABM và tam giác ACM có :

AM chung

BM = CM ( M là trung điểm BC )

AB = AC (tam giác ABC cân tại A theo giả thiết)

\( \Rightarrow \Delta AMB = \Delta AMC (c-c-c)\)

\( \Rightarrow \widehat{BAM}= \widehat{CAM}\) (2 góc tương ứng)

\( \Rightarrow \) AM thuộc tia phân giác của góc A

Mà AM cắt tia phân giác góc B tại I

\( \Rightarrow \) I là giao của các đường phân giác trong tam giác ABC

\( \Rightarrow \) CI là phân giác góc C (định lí 3 đường phân giác cắt nhau tại 1 điểm)

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 15 phiếu

Bài tiếp theo

Giải bài 3 trang 82 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC cân tại A. Tia phân giác của các góc B và C cắt nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC
Giải bài 4 trang 82 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thằng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN.
Giải bài 5 trang 82 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác AMN vuông tại A. Tia phân giác của góc M và N cắt nhau tại I. Tia MI cắt AN tại R. Kẻ RT vuông góc với AI tại T. Chứng minh rằng AT = RT.
Giải bài 6 trang 82 SGK Toán 7 tập 2 - Chân trời sáng tạo
Ba thành phố A, B, C được nối với nhau bởi xa lộ (Hình 9). Người ta muốn tìm một địa điểm để làm một sân bay sao cho địa điểm này phải cách đều ba xa lộ đó. Hãy xác định vị trí của sân bay thỏa mãn điều kiện trên và giải thích cách thực hiện.
Giải bài 1 trang 81 SGK Toán 7 tập 2 - Chân trời sáng tạo
Trong Hình 8, I là giao điểm của ba đường phân giác của tam giác ABC. a) Cho biết IM = 6 (Hình 8a). Tính IK và IN. b) Cho biết IN = x + 3, IM = 2x – 3 (Hình 8b). Tìm x
Giải mục 2 trang 79 SGK Toán 7 tập 2 - Chân trời sáng tạo
Vẽ một tam giác trên giấy. Cắt rời tam giác ra khỏi tờ giấy rồi gấp hình tam giác đó để xác định ba đường phân giác của tam giác (Hình 4). Em hãy quan sát và nhận xét xem ba đường phân giác có cùng đi qua một điểm không.
Giải mục 1 trang 79 SGK Toán 7 tập 2 - Chân trời sáng tạo
Vẽ và cắt hình tam giác ABC rồi gấp hình sao cho cạnh AB trùng với cạnh AC ta được nếp gấp AD (Hình 1). Đoạn thẳng AD nằm trên tia phân giác của góc nào của tam giác ABC ?