Giải bài 2 trang 77 SGK Toán 10 tập 1 – Chân trời sáng tạo

Để lắp đường dây diện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8km. Góc tạo bởi hai đoạn dây AC và CB là 70. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Đề bài

Để lắp đường dây diện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8km. Góc tạo bởi hai đoạn dây AC và CB là \({70^o}\). Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.

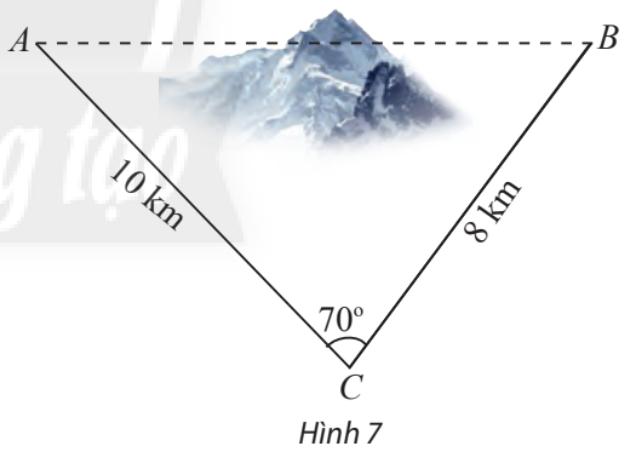
Phương pháp giải - Xem chi tiết

Bước 1: Tính cạnh AB: Áp dụng định lí cosin: \(A{B^2} = B{C^2} + A{C^2} - 2.BC.AC.\cos C\)

Bước 2: Tính chiều dài tăng thêm, bằng \(AC + CB - AB\)

Lời giải chi tiết

Áp dụng định lí cosin, ta có:

\(\begin{array}{l}A{B^2} = B{C^2} + A{C^2} - 2.BC.AC.\cos C\\ \Leftrightarrow A{B^2} = {8^2} + {10^2} - 2.8.10.\cos {70^o}\\ \Rightarrow AB \approx 10,45\end{array}\)

Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:

\(AC + CB - AB = 10 + 8 - 10,45 = 7,55\;(km).\)

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 16 phiếu

Bài tiếp theo

Giải bài 3 trang 77 SGK Toán 10 tập 1 – Chân trời sáng tạo
Một người đứng cách thân một các quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng 56,5 (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là 1,5m.
Giải bài 4 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là
Giải bài 5 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo
Hai người quan sát khinh khí cầu tại hai địa điểm P và Q nằm ở sườn đồi nghiêng 32 so với phương ngang, cách nhau 60 m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là
Giải bài 6 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo
Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt dất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là
Giải bài 1 trang 77 SGK Toán 10 tập 1 – Chân trời sáng tạo
Giải tam giác ABC trong các trường hợp sau:
Giải mục 2 trang 75, 76, 77 SGK Toán 10 tập 1 - Chân trời sáng tạo
Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên.
Giải mục 1 trang 74, 75 SGK Toán 10 tập 1 - Chân trời sáng tạo
Giải tam giác ABC trong các trường hợp sau:
Lý thuyết Giải tam giác và ứng dụng thực tế
Giải tam giác là tìm số đo các cạnh và các góc chưa biết của tam giác.