Đề thi vào lớp 6 môn Toán trường THCS Lương Thế Vinh tỉnh Thái Bình năm 2025

Đề bài

 ĐỀ TUYỂN SINH LỚP 6 TRƯỜNG THCS LƯƠNG THẾ VINH - TP THÁI BÌNH 

NĂM HỌC 2025 - 2026

MÔN: TOÁN

Thời gian làm bài: 60 phút

I. Trắc nghiệm (6 điểm):

Chọn một chữ cái đứng trước câu trả lời đúng và ghi vào giấy kiểm tra.

Câu 1 (1 điểm). 20% được viết dưới dạng phân số tối giản là:

A. $\frac{{20}}{{100}}$$$                              B. $\frac{5}{{100}}$                            C. $\frac{1}{5}$                             D. $\frac{1}{4}$         

 Câu 2 (1 điểm). 4 giờ 40 phút = ….. giờ:

A. 4,4                                  B. $\frac{{14}}{3}$                             C. $\frac{7}{3}$                              D. $\frac{{11}}{3}$

Câu 3 (1 điểm). Hiệu giá trị của hai chữ số 3 trong số thập phân 35,36 là:

A. 30,3                                B. 29,7                           C. 9                                D. 300

Câu 4 (1 điểm). Gieo một con xúc xắc 10 lần liên tiếp có kết quả như sau:

Tỉ số giữa số lần xuất hiện mặt lẻ và tổng số lần gieo xúc xắc là:

A. $\frac{3}{{10}}$                                 B. $\frac{3}{7}$                               C. $\frac{4}{7}$                            D. $\frac{7}{{10}}$

Ghi đáp số của các câu 5, 6 vào giấy kiểm tra (không phải trình bày lời giải)

Câu 5 (1 điểm). Tổng độ dài các cạnh của một hình lập phương là 7,2cm. Tính diện tích toàn phần của hình lập phương đó.

Câu 6 (1 điểm). Mai và An là hai chị em sinh đôi và họ có một anh trai. Tổng số tuổi của ba anh

em là 50 tuổi. Tìm tuổi của Mai biết tuổi của anh trai bằng $\frac{4}{3}$ tuổi của Mai.

II. Tự luận (14 điểm):

Bài 1 (4 điểm).

a. Tính giá trị của biểu thức: $0,75 \times 1\frac{1}{2} + \frac{3}{{17}}:\frac{5}{{34}}$

b. Tìm qui luật và tìm số thứ 50 của dãy số sau:

3; 5; 8; 12 ; 17; ...

Bài 2 (2 điểm). So sánh A và B biết $A = \frac{{2024}}{{2025}} + \frac{{2025}}{{2026}} + \frac{{2026}}{{2024}}$ và $B = \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ..... + \frac{1}{{15}}$

Bài 3 (2 điểm). Hai người khởi hành từ hai địa điểm A, B và đi ngược chiều nhau.

a. Nếu hai người xuất phát cùng một lúc thì họ gặp nhau tại một điểm cách A 40 km và cách B 60 km. Tính quãng đường AB.

b. Nếu hai người muốn gặp nhau tại điểm C sao cho quãng đường AC ngắn hơn quãng đường BC là 8km thì người đi từ A phải khởi hành trước người đi từ B là 15 phút. Tính vận tốc của người đi từ A.

Bài 4 (6 điểm). Cho tam giác ABC. Trên AB lấy M sao cho AM = $\frac{2}{3}$AB; Lấy N là trung điểm của AC; BN cắt CM tại I.

a. Tinh diện tích tam giác AMC biết diện tích tam giác ABC là 600cm².

b. Tìm tỉ số diện tích tam giác AMN và diện tích tam giác BNC.

c. Chứng tỏ rằng I là trung điểm của BN.

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

I. Trắc nghiệm

Câu 1 (1 điểm). 20% được viết dưới dạng phân số tối giản là:

A. $\frac{{20}}{{100}}$                              B. $\frac{5}{{100}}$                            C. $\frac{1}{5}$                             D. $\frac{1}{4}$       

Cách giải

20% = $\frac{{20}}{{100}} = \frac{1}{5}$

Đáp án: C 

 Câu 2 (1 điểm). 4 giờ 40 phút = ….. giờ:

A. 4,4                                  B. $\frac{{14}}{3}$                             C. $\frac{7}{3}$                              D. $\frac{{11}}{3}$

Cách giải:

4 giờ 40 phút = $4\frac{{40}}{{60}}$ giờ = $4\frac{2}{3}$ giờ = $\frac{{14}}{3}$ giờ

Đáp án: B

Câu 3 (1 điểm). Hiệu giá trị của hai chữ số 3 trong số thập phân 35,36 là:

A. 30,3                                B. 29,7                           C. 9                                D. 300

Cách giải:

Hiệu giá trị của hai chữ số 3 trong số thập phân 35,36 là 30 – 0,3 = 29,7

Đáp án: B

Câu 4 (1 điểm). Gieo một con xúc xắc 10 lần liên tiếp có kết quả như sau:

 Tỉ số giữa số lần xuất hiện mặt lẻ và tổng số lần gieo xúc xắc là:

A. $\frac{3}{{10}}$                                 B. $\frac{3}{7}$                               C. $\frac{4}{7}$                            D. $\frac{7}{{10}}$

Cách giải

Số lần xuất hiện mặt lẻ là 7.

Tỉ số giữa số lần xuất hiện mặt lẻ và tổng số lần gieo xúc xắc là: $\frac{7}{{10}}$

Đáp án: D

Câu 5 (1 điểm). Tổng độ dài các cạnh của một hình lập phương là 7,2cm. Tính diện tích toàn phần của hình lập phương đó.

Cách giải:

Độ dài 1 cạnh của hình lập phương là: 7,2 : 12 = 0,6 (cm)

Diện tích toàn phần của hình lập phương đó là 0,6 x 0,6 x 6 = 2,16 (cm²)

Đáp số: 2,16 cm²

Câu 6 (1 điểm). Mai và An là hai chị em sinh đôi và họ có một anh trai. Tổng số tuổi của ba anh

em là 50 tuổi. Tìm tuổi của Mai biết tuổi của anh trai bằng $\frac{4}{3}$ tuổi của Mai.

Cách giải:

Mai và An là hai chị em sinh đôi nên Mai và An có số tuổi bằng nhau.

Tuổi của anh trai bằng $\frac{4}{3}$ tuổi của Mai.

 Hay tuổi của anh trai bằng $\frac{4}{{3 + 3 + 4}} = \frac{4}{{10}} = \frac{2}{5}$ (tổng số tuổi của ba anh em)

Tuổi của anh trai là $50 \times \frac{2}{5} = 20$ (tuổi)

Tuổi của Mai là (50 – 20) : 2 = 15 (tuổi)

Đáp số: 15 tuổi

II. Tự luận

Bài 1 (4 điểm).

a. Tính giá trị của biểu thức: $0,75 \times 1\frac{1}{2} + \frac{3}{{17}}:\frac{5}{{34}}$

b. Tìm qui luật và tìm số thứ 50 của dãy số sau:

3; 5; 8; 12 ; 17; ...

Cách giải:

a) $0,75 \times 1\frac{1}{2} + \frac{3}{{17}}:\frac{5}{{34}}$ = $\frac{3}{4} \times \frac{3}{2} + \frac{3}{{17}} \times \frac{{34}}{5} = \frac{9}{8} + \frac{6}{5} = \frac{{45}}{{40}} + \frac{{48}}{{40}} = \frac{{93}}{{40}}$

b) Quy luật:

Số thứ 1 là 3 = 2 + 1

Số thứ 2 là 5 = 2 + 1 + 2

Số thứ 3 là 8 = 2 + 1 + 2 + 3

Số thứ 4 là 12 = 2 + 1 + 2 + 3 + 4

Số thứ 5 là 17 = 2 + 1 + 2 + 3 + 4 + 5

.....

Số thứ 50 là 2 + 1 + 2 + 3 + 4 + 5 + ..... + 50

Xét A = 1 + 2 + 3 + 4 + 5 + ..... + 50

Số số hạng của dãy trên là (50 – 1) : 1 + 1 = 50 (số hạng)

A = (50 + 1) x 50 : 2 = 1275

Vậy số thứ 50 của dãy đã cho là 2 + 1275 = 1277

Đáp số: 1277

Bài 2 (2 điểm). So sánh A và B biết $A = \frac{{2024}}{{2025}} + \frac{{2025}}{{2026}} + \frac{{2026}}{{2024}}$ và $B = \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ..... + \frac{1}{{15}}$

Cách giải:

$A = \frac{{2024}}{{2025}} + \frac{{2025}}{{2026}} + \frac{{2026}}{{2024}}$

$A = 1 - \frac{1}{{2025}} + 1 - \frac{1}{{2026}} + 1 + \frac{2}{{2024}}$

A = 3 + $\frac{2}{{2024}} - \left( {\frac{1}{{2025}} + \frac{1}{{2026}}} \right)$

Ta thấy $\frac{2}{{2024}} = \frac{1}{{2024}} + \frac{1}{{2024}}$ nên $\frac{2}{{2024}} - \left( {\frac{1}{{2025}} + \frac{1}{{2026}}} \right) > 0$

Suy ra A > 3

$B = \frac{1}{2} + (\frac{1}{3} + \frac{1}{4} + \frac{1}{5}) + (\frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \frac{1}{9} + \frac{1}{{10}} + \frac{1}{{11}}) + (\frac{1}{{12}} + \frac{1}{{13}} + \frac{1}{{14}} + \frac{1}{{15}})$

Ta thấy $\frac{1}{3} + \frac{1}{4} + \frac{1}{5} < \frac{1}{3} + \frac{1}{3} + \frac{1}{3} < 1$

$\frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \frac{1}{9} + \frac{1}{{10}} + \frac{1}{{11}} < \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} < 1$

$\frac{1}{{12}} + \frac{1}{{13}} + \frac{1}{{14}} + \frac{1}{{15}} < \frac{1}{{12}} + \frac{1}{{12}} + \frac{1}{{12}} + \frac{1}{{12}} < \frac{1}{3}$

Vậy B < $\frac{1}{2} + 1 + 1 + \frac{1}{3}$< 3

Vậy A > B

Bài 3 (2 điểm). Hai người khởi hành từ hai địa điểm A, B và đi ngược chiều nhau.

a. Nếu hai người xuất phát cùng một lúc thì họ gặp nhau tại một điểm cách A 40 km và cách B 60 km. Tính quãng đường AB.

b. Nếu hai người muốn gặp nhau tại điểm C sao cho quãng đường AC ngắn hơn quãng đường BC là 8km thì người đi từ A phải khởi hành trước người đi từ B là 15 phút. Tính vận tốc của người đi từ A.

Cách giải

a) Quãng đường AB là 40 + 60 = 100 (km)

b) Độ dài quãng đường AC là (100 – 8) : 2 = 46 (km)

Quãng đường BC là 100 – 46 = 54 (km)

Vì vận tốc của 2 người không đổi và trong cùng thời gian thì quãng đường tỉ lệ thuận với vận tốc

Suy ra $\frac{{{v_A}}}{{{v_B}}} = \frac{{{S_A}}}{{{S_B}}} = \frac{{40}}{{60}} = \frac{2}{3}$

Trong cùng một khoảng thời gian, khi người đi từ B đi được 54 km thì người đi từ A đi được $54 \times \frac{2}{3} = 36$ (km)

Quãng đường người đi từ A đi trước là 46 – 36 = 10 (km)

Vận tốc của người đi từ A là 10 : 0,25 = 40 (km/giờ)

Đáp số: a) 100 km

            b) 40 km/giờ

Bài 4 (6 điểm). Cho tam giác ABC. Trên AB lấy M sao cho AM = $\frac{2}{3}$AB; Lấy N là trung điểm của AC; BN cắt CM tại I.

a. Tinh diện tích tam giác AMC biết diện tích tam giác ABC là 600cm².

b. Tìm tỉ số diện tích tam giác AMN và diện tích tam giác BNC.

c. Chứng tỏ rằng I là trung điểm của BN.

Cách giải

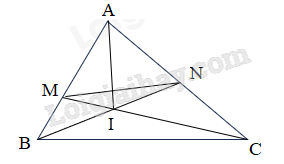
a) S_AMC = $\frac{2}{3}$S_ABC (Chung chiều cao hạ từ C và đáy AM = $\frac{2}{3}$AB)$$

Suy ra S_AMC = $\frac{2}{3} \times 600 = 400$ (cm²)

b) Ta có S_ABN = S_BNC = $\frac{1}{2}$ S_ABC (Chung chiều cao hạ từ đỉnh B và đáy AN = NC)

S_AMN = $\frac{2}{3}$S_ABN (Chung chiều cao hạ từ N và đáy AM = $\frac{2}{3}$AB)$$

Suy ra S_AMN = $\frac{2}{3}$S_BNC

c)  Ta có S_ABN = S_BNC nên chiều cao hạ từ A xuống BN = chiều cao hạ từ C xuống BN.

$ \Rightarrow $S_ABI = S_BIC (Chung đáy BI và chiều cao hạ từ A xuống BN = chiều cao hạ từ C xuống BN) (1)

Ta có S_BMC = $\frac{1}{2}$S_AMC (Chung chiểu cao hạ từ C và đáy BM = $\frac{1}{2}$AM)

Suy ra chiều cao hạ từ B xuống MC = $\frac{1}{2}$chiều cao hạ từ A xuống MC

$ \Rightarrow $S_BIC = $\frac{1}{2}$S_AIC (Chung đáy IC và chiều cao hạ từ B xuống MC = $\frac{1}{2}$chiều cao hạ từ A xuống MC) (2)

Ta có S_AIN = $\frac{1}{2}$S_AIC (Chung chiểu cao hạ từ I và đáy AN = $\frac{1}{2}$AC) (3)

Từ (1), (2), (3) suy ra S_ABI = S_AIN

Vậy BI = IN (Hai tam giác bằng nhau có chung chiều cao hạ từ A)

Vậy I là trung điểm của BN.