Đề thi học kì 1 Toán 8 Cánh diều - Đề số 8

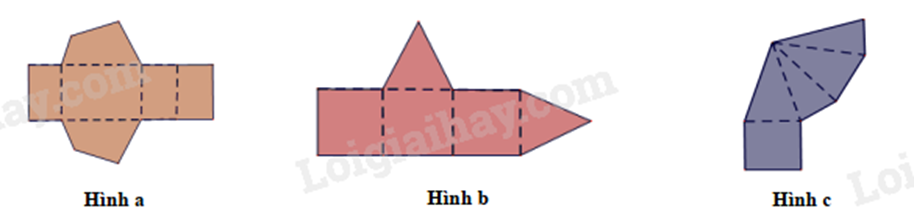
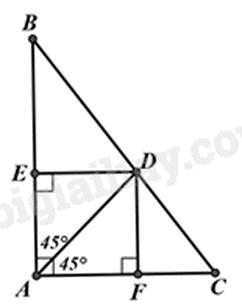
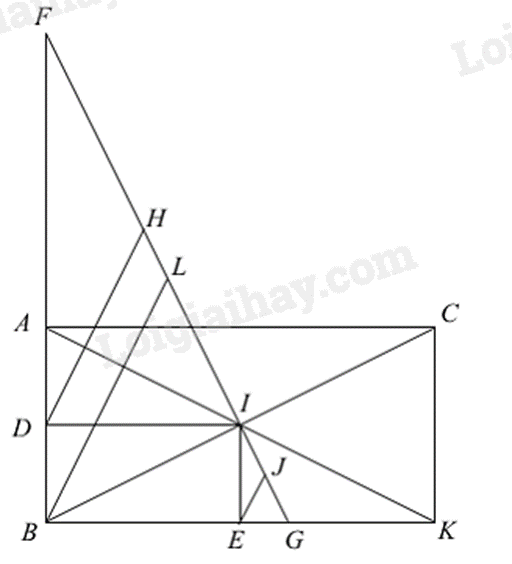
a) Xét tứ giác ABKC có:

AK và BC cắt nhau tại I

I là trung điểm của AK ( K đối xứng với A qua I)

I là trung điểm của BC

Suy ra ABKC là hình bình hành

Mà tam giác ABC vuông tại A nên \(\widehat A = 90^\circ \), suy ra ABKC là hình chữ nhật.

b) Vì ABCD là hình chữ nhật nên AI = IB, suy ra tam giác AIB cân tại I.

Vì D là trung điểm của AB nên ID là đường trung tuyến của tam giác AIB, do đó ID đồng thời là đường cao của tam giác AIB nên \(ID \bot AB\) hay \(\widehat {IDB} = 90^\circ \).

Chứng minh tương tự ta có \(IE \bot BK\) hay \(\widehat {BEI} = 90^\circ \).

ABCD là hình chữ nhật nên \(\widehat {DBE} = 90^\circ \).

Xét tứ giác BDIE, ta có:

\(\widehat {IDB} = \widehat {DBE} = \widehat {BEI} = 90^\circ \) nên BDIE là hình chữ nhật. Do đó ID = BE.

Mà BE = EK = \(\frac{1}{2}\)BK nên ID = \(\frac{1}{2}\)BK.

c) Xét tam giác vuông FDI có H là trung điểm của FI nên DH là đường trung tuyến ứng với cạnh huyền của tam giác FDI.

Do đó DH = FH, suy ra tam giác DHF cân tại H. Từ đó suy ra \(\widehat {DFH} = \widehat {FDH}\) (1).

Chứng minh tương tự, ta có tam giác FLB cân tại L, suy ra \(\widehat {BFL} = \widehat {FBL}\) (2).

Từ (1) và (2) suy ra \(\widehat {FDH} = \widehat {FBL}\). Mà hai góc này ở vị trí đồng vị nên DH // BL (3).

Chứng minh tương tự, ta được BL // EJ (4).

Từ (3) và (4) suy ra DH // EJ.