Tìm giá trị lớn nhất của phân thức: \(A = \frac{5}{{4{x^2} - 12x + 14}}\).
Biến đổi mẫu thức để đánh giá phân thức sao cho \(A\left( x \right) \le M\).
Giá trị lớn nhất của biểu thức là M, giải để tìm x.
Ta có: \(4{x^2} - 12x + 14 = {\left( {2x} \right)^2} - 2.2x.3 + 9 + 5 = {\left( {2x - 3} \right)^2} + 5\)
Vì \({\left( {2x - 3} \right)^2} \ge 0\) với mọi \(x\) nên \({\left( {2x - 3} \right)^2} + 5 \ge 5\)
Do đó \(A = \frac{5}{{4{x^2} - 12x + 14}} = \frac{5}{{{{\left( {2x - 3} \right)}^2} + 5}} \le \frac{5}{5} = 1\)
Dấu “=” xảy ra khi \(2x - 3 = 0\) suy ra \(x = \frac{3}{2}\).
Vậy giá trị lớn nhất của phân thức A là 1 khi \(x = \frac{3}{2}\).

Các bài tập cùng chuyên đề
Cho biểu thức \(P = \frac{{{x^2} - 1}}{{2x + 1}}\)
a) Tính giá trị của biểu thức tại \(x = 0\)
b) Tại \(x = - \frac{1}{2}\), giá trị của biểu thức có xác định không? Tại sao?
Tìm giá trị của phân thức:
a) \(\dfrac{{{x^2} - 2x + 1}}{{x + 2}}\) tại \(x = - 3\), \(x = 1\)
b) \(\dfrac{{xy - 3{y^2}}}{{x + y}}\) tại \(x = 3\), \(y = - 1\)
Giá thành trung bình của một chiếc áo sơ mi được một xí nghiệp sản xuất cho bởi biểu thức \(C(x) = \dfrac{{0,0002{x^2} + 120x + 1000}}{x}\), trong đó \(x\) là số áo được sản xuất và \(C\) tính bằng nghìn đồng. Tính \(C\) khi \(x = 100\), \(x = 1000\)
Tìm giá trị của phân thức:
a) \(A = \dfrac{{3{x^2} + 3x}}{{{x^2} + 2x + 1}}\) tại \(x = - 4\)
b) \(B = \dfrac{{ab - {b^2}}}{{{a^2} - {b^2}}}\) tại \(a = 4\), \(b = - 2\)
Tính giá trị của biểu thức \(\frac {x+2}{x-1}\) tại x = 4.
Cho phân thức: \(\dfrac{{x + 1}}{{{x^2} + x}}\)
a) Viết điều kiện của x để giá trị của phân thức được xác định.
b) Tính giá trị của phân thức tại x = 1 và x = 10.
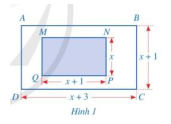
Cho hình chữ nhật ABCD và MNPQ như hình 1 (các số đo trên hình tính theo đơn vị centimét).
a) Viết phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNPQ.
b) Tính giá trị của phân thức đó tại x = 2 và tại x = 5.
Chị Hà mở một xưởng thủ công với số vốn đầu tư ban đầu (xây dựng nhà xưởng, mua máy móc,…) là 80 triệu đồng. Biết chi phí để sản xuất (tiền mua vật liệu, lương công nhân) của 1 sản phẩm là 15 nghìn đồng. Gọi x là số sản phẩm mà xưởng của chị Hà làm được.
a) Viết phân thức biểu thị số tiền thực (đơn vị nghìn đồng) để tạo 1 sản phẩm theo x.
b) Tính chi phí thực tế để tạo ra 1 sản phẩm nếu x = 100; x = 1 000. Nhận xét về chi phí thực để tạo 1 sản phẩm nếu x ngày càng tăng.
Trong chuyển động đều, nếu một vật di chuyển với tốc độ \(v\left( {m/s} \right)\) và đi được một quãng đường \(S\left( m \right)\) thì biểu thức \(\frac{S}{v}\) cho biết thời gian vật di chuyển hết quãng đường đó.
a) Khi vật di chuyển với tốc độ \(v = 2\left( {m/s} \right)\), tính thời gian vật di chuyển hết quãng đường \(S = 50\left( m \right).\)
b) Vì sao không thể xác định được giá trị của biểu thức \(\frac{S}{v}\) khi \(v = 0\left( {m/s} \right).\)
Hãy trả lời câu hỏi phần khởi động:
Ta đã biết khoảng cách \(q\) từ ống kính máy ảnh ( hay vật kính) đến phim được tính bởi công thức \(q = \frac{{df}}{{d - f}}\) trong đó \(d\) là khoảng cách từ vật đến ống kính máy ảnh( hay vật kính), \(f\) là tiêu cự của ống kính ( hay vật kính).
a) Vì sao không thể xác định được giá trị của \(q\) trong công thức trên khi \(d = f\)?
b) Khi khoảng cách từ vật đến ống kính máy ảnh bằng \(40cm\) và tiêu cự của ống kính bằng \(8cm\) thì khoảng cách từ ống kính máy ảnh đến phim bằng bao nhiêu?
Cho phân thức \(\frac{{3 - 2d}}{d}\)
a) Viết điều kiện xác định của phân thức
b) So sánh giá trị của phân thức tại \(d = 1\) và \(d = - 1.\)
Một cửa hàng chuyên bán các loại hạt có bán các gói loại A, mỗi gói bao gồm 100 gam hạt đậu phộng và 80 gam hạt điều. Sau đó cửa hàng tung ra các gói loại B bằng cách cho thêm \(x\) gam hạt đậu phộng vào mỗi gói loại A. Giả sử khối lượng bao bì mỗi gói không đáng kể.
a) Xét một gói loại B, hãy viết một phân thức biểu diễn tỉ số khối lượng của đậu phộng và cả gói.
b) Tỉ số khối lượng nêu ở câu a là bao nhiêu khi cho thêm 20 gam hạt đậu phộng vào mỗi gói loại A?
Một công ty sử dụng công thức \(S = \frac{{150n + 50}}{{n + 1}}\) (đơn vị: triệu đồng) để xã định tổng tiền lương của nhân viên X trong năm thứ \(n\) tại công ty.
a) Xác định tổng tiền lương của nhân viên X trong năm đầu tiên.
b) Xác định tổng tiền lương của nhân viên X trong năm thứ tư.
Cho phân thức \(\frac{{\left( {36 - a} \right)\left( {a - 1} \right)}}{{a - 3}}\).
a) Viết điều kiện xác định của phân thức.
b) So sánh giá trị của phân thức tại \(a = 0\) và \(a = 2\).
Giả sử chi phí C (USD) mà một nhà máy cần phải trả để giảm \(p\% \) chất ô nhiễm được tính bởi công thức: \(C = \frac{{1200p}}{{1 - 0,01p}}\)
a) Viết điều kiện xác định của phân thức C.
b) Tính chi phí nhà máy cần phải trả để giảm được 75% chất ô nhiễm.
Cho phân thức \(P = \frac{{2x + 4}}{{{x^2} + 2x}}\).
a) Viết điều kiện xác định của phân thức đã cho.
b) Tìm giá trị của phân thức tại \(x = 0\) và tại \(x = - 1\).
Tìm giá trị của phân thức \(Q = \frac{{3x + 3y}}{{{x^2} - {y^2}}}\) tại:
a) \(x = 2\) và \(y = 1\);
b) \(x = 2\) và \(y = - 2\);
Tính giá trị của biểu thức:
a) \(A = \frac{{{x^5}{y^2}}}{{{{\left( {xy} \right)}^3}}}\) tại \(x = 1;y = 2\)
b) \(B = \frac{{ - 4\left( {x - 2} \right){x^2}}}{{20\left( {2 - x} \right){y^2}}}\) tại \(x = \frac{1}{2};y = \frac{1}{5}\).
c) \(C = \frac{{{x^2} - 8x + 7}}{{{x^2} - 1}}\) tại \(x = - 7\)
d) \(D = \frac{{5{x^2} - 10xy + 5{y^2}}}{{{x^2} - {y^1}}}\) tại \(x = 0,5;y = 0,6\).
Một miếng bìa có dạng hình vuông với độ dài xạnh là \(x\) (cm). Người ta cắt đi ở mỗi góc của miếng bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh là \(y\) (cm) với \(0 < 2y < x\) (Hình 2).
a) Viết phân thức biểu thị tỉ số diện tích của miếng bìa ban đầu và phần miếng bìa còn lại sau khi bị cắt.
b) Tính giá trị của phân thức đó tại \(x = 4;y = 1\)

Viết điều kiện xác định của phân thức \(\frac{{{x^2} + x - 2}}{{x + 2}}\). Tính giá trị của phân thức đó lần lượt tại x = 0; x = 1; x = 2.
Cho A là một đa thức khác 0 tùy ý. Hãy giải thích vì sao \(\frac{0}{A} = 0\) và \(\frac{A}{A} = 1\)
Cho phân thức \(P = \frac{{{x^3} - 4{\rm{x}}}}{{{{(x + 2)}^2}}}\)
a) Viết điều kiện xác định của phân thức và tìm tất cả các giá trị của x thỏa mãn điều kiện này.
b) Rút gọn phân thức P.
c) Tính giá trị của phân thức đã cho tại x = 98.
Lúc 6 giờ sáng, bác Vinh lái ô tô xuất phát từ Hà Nội đi huyện Tĩnh Gia (Thanh Hóa). Khi đến Phủ Lý (Hà Nam), cách Hà Nội khoảng 60 Km, bác Vinh dừng lại ăn sáng trong 20 phút. Sau đó, bác Vinh tiếp tục đi về Tĩnh Gia và phải tăng tốc thêm 10Km/h để đến nơi đúng giờ dự định.
a) Gọi x (Km/h) là vận tốc đi thêm trên quãng đường Hà Nội – Phủ Lý. Hãy viết các phân thức biểu thị thời gian bác Vinh chạy xe trên các quãng đường Hà Nội – Phủ Lý và Phủ Lý – Tĩnh Gia, biết rằng quãng đường Hà Nội – Tĩnh Gia có chiều dài khoảng 200 Km.
b) Nếu vận tốc ô tô đi trên quãng đường Hà Nội – Phủ Lý là 60 Km/h thì bác Vinh đến Tĩnh Gia lúc mấy giờ?
Để loại bỏ x (tính theo %) chất gây ô nhiễm không khí từ khí thải của một nhà máy, ước tính cần chi phí là \(\frac{{1,7{\rm{x}}}}{{100 - x}}\)(tỉ đồng).
a) Nếu muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là bao nhiêu?
b) Viết điều kiện xác định của phân thức \(\frac{{1,7{\rm{x}}}}{{100 - x}}\). Hỏi có thể loại bỏ được 100% chất gây ô nhiễm từ khí thải nhà máy hay không?
Cho phân thức: \(P = \frac{{2{\rm{x}} + 1}}{{x + 1}}\)
a) Viết điều kiện xác định của P
b) Hãy viết P dưới dạng \(a - \frac{b}{{x + 1}}\), trong đó a, b là số nguyên dương
c) Với giá trị nào của x thì P có giá trị là số nguyên
Một xe ô tô đi từ Hà Nội đến Vinh với vận tốc 60km/h và dự kiến sẽ đến Vinh sau 5 giờ chạy. Tuy nhiên, sau \(2\frac{2}{3}\) giờ chạy với vận tốc 60km/h, xe dừng nghỉ 20 phút. Sau khi dừng nghỉ, để đến Vinh đúng thời gian dự kiến, xe phải tăng vận tốc so với chặng đầu
a) Tính độ dài quãng đường Hà Nội - Vinh
b) Tính độ dài quãng đường còn lại sau khi dừng nghỉ
c) Cho biết ở chặng thứ hai xe tăng vận tốc thêm x (km/h). Hãy viết biểu thức P biểu thị thời gian (tính bằng giờ) thực tế xe chạy hết chặng đường Hà Nội - Vinh
d) Tính thời gian của P lần lượt tại x = 5, x = 10; x = 15, từ đó cho biết ở chặng thứ hai (sau khi xe dừng nghỉ):
- Nếu tăng vận tốc thêm 5km/h thì xe đến Vinh muộn hơn dự kiến bao nhiêu giờ?
- Nếu tăng vận tốc thêm 10km/h thì xe đến Vinh có đúng thời gian dự kiến không?
- Nếu tăng vận tốc thêm 15km/h thì xe đến Vinh sớm hơn dự kiến bao nhiêu giờ?
Giá trị của x để phân thức \(\frac{{x - 2}}{5}\) có giá trị bằng \(0\) là:
-
A.
1
-
B.
2
-
C.
3
-
D.
-1
Tìm tập hợp các giá trị nguyên của x sao cho \(P\left( x \right) = \frac{2}{{x + 1}}\) có giá trị là số nguyên.
Giá trị của phân thức \(\frac{{8x - 4}}{{8{x^3} - 1}}\) tại \(x = - 0,5\) là:
A. 4
B. -4
C. 0,25
D. -0,25
Cho phân thức \(P = \frac{{{x^2} - 4x + 3}}{{{x^2} - 9}}\)
a) Viết điều kiện xác định của phân thức. Tìm tập hợp tất cả các giá trị của x không thỏa mãn điều kiện xác định.
b) Rút gọn phân thức đã cho.
c) Tìm tập hợp tất cả các giá trị nguyên của x để phân thức P nhận giá trị là một số nguyên.







Danh sách bình luận