Đề kiểm tra 15 phút - Đề số 8 - Bài 6 - Chương 2 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 8 - Bài 6 - Chương 2 - Hình học 7
Đề bài
Cho tam giác ABC cân tại A, vẽ \(EC = EH + HC \Rightarrow EC = MI + MJ\) \(MI \bot AB\) (E thuộc AB). Lấy M thuộc đoạn BC, vẽ \(MI \bot AB\) và \(MJ \bot AC\) (I thuộc AB, J thuộc AC). Chứng minh \(MI + MJ = CE\)
Phương pháp giải - Xem chi tiết
Nối M với E, Kẻ \(MH \bot CE\)
Chứng minh MI=EH và MJ=HC
Lời giải chi tiết
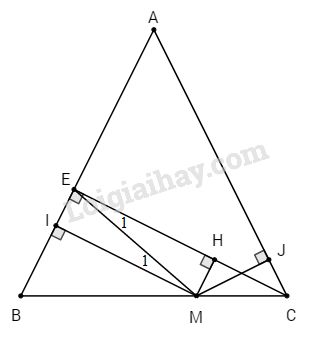
Nối M với E. Ta có \(MI \bot AB\) (giả thiết); \(CE \bot AB\) (giả thiết) \(\Rightarrow MI//CE\).
Do đó \(\widehat {EMI} = \widehat {MEC}\) (1) (cặp góc so le trong).
Kẻ \(MH \bot CE\),
Xét hai tam giác vuông MIE và EHM có:
+) ME chung
+) \(\widehat {EMI} = \widehat {MEC}\)
\(\Rightarrow \Delta MIE = \Delta EHM\) (g.c.g)
\(\Rightarrow MI = EH\) (cạnh tương ứng)
Mặt khác MH // AB (cùng vuông góc với EC)
\( \Rightarrow \widehat {CMH} = \widehat {CBA} = \widehat {BCA}\) (2) (cặp góc đồng vị).
Xét hai tam giác vuông MHC và CJM có:
+) MC chung
+) \( \widehat {CMH} = \widehat {BCA}\)
\( \Rightarrow \Delta MHC = \Delta CJM\) (g.c.g).
Do đó \(MJ = HC\), mà \(EC = EH + HC \)
\(\Rightarrow EC = MI + MJ.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 7 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 5 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 2 - Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
