Bài 52 trang 128 SGK Toán 7 tập 1
Cho góc xOy có số đo, điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox(B thuộc Ox), kẻ AC vuông góc với Oy(C thuộc Oy).
Đề bài
Cho góc \(xOy\) có số đo \(120^0\), điểm \(A\) thuộc tia phân giác của góc đó. Kẻ \(AB\) vuông góc với \(Ox\) (\(B\) thuộc \(Ox\)), kẻ \(AC\) vuông góc với \(Oy\) (\(C\) thuộc \(Oy\)). Tam giác \(ABC\) là tam giác gì ? Vì sao?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Nếu cạnh huyền và góc nhọn của tam giác vuông này bằng cạnh huyền, góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Tam giác cân có một góc bằng \(60^o\) thì tam giác đó là tam giác đều.
- Định lí tổng ba góc của một tam giác bằng \(180^o\).
Lời giải chi tiết
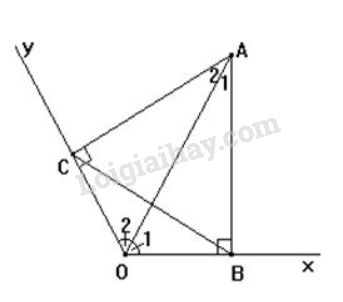
Tam giác \(ACO\) vuông tại \(C\).
Tam giác \(ABO\) vuông tại \(B\)
Xét hai tam giác vuông \(ACO\) và \(ABO\) có:
+) \(\widehat{O_{1}}=\widehat{O_{2}}\) (Vì \(OA\) là tia phân giác góc \(xOy\))
+) \(AO\) chung
\( \Rightarrow ∆ACO=∆ABO\) (cạnh huyền-góc nhọn)
\(\Rightarrow AC=AB\) (hai cạnh tương ứng); \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng)
Ta có \(\widehat {{O_1}} = \dfrac{1}{2}\widehat {xOy} = \dfrac{1}{2}{.120^0} = {60^0}\) (vì \(OA\) là tia phân giác góc \(xOy\))
Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta OBA\) ta có:
\(\eqalign{
& \widehat {{O_1}} + \widehat B + \widehat {{A_1}} = {180^0} \cr
& \Rightarrow \widehat {{A_1}} = {180^0} - \widehat {{O_1}} - \widehat B \cr&\;\;\;\;\;\;\;\;\;\;= {180^0} - {60^0} - {90^0} = {30^0} \cr} \)
Do đó: \(\widehat {{A_1}} = \widehat {{A_2}} = {30^0}\)
Hay \(\widehat {BAC} = \widehat {{A_1}} + \widehat {{A_2}} \)\(=30^0+30^0= {60^0}\)
Vì \(∆ABC\) có \(AC=AB\) nên \(∆ABC\) cân tại \(A\).
Mà \(\widehat {BAC}= {60^0}\) nên \(∆ABC\) là tam giác đều.
- Đề kiểm tra 15 phút - Đề số 1 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 5 - Bài 6 - Chương 2 - Hình học 7
>> Xem thêm














Danh sách bình luận