Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 7
Đề bài
Cho tam giác ABC vuông cân tại A. Trên đáy BC lấy hai điểm M, N sao cho \( \Rightarrow AM = AN.\) \(BM = CN = AB.\)
a) Chứng minh \(\Delta AMN\) cân.
b) Tính \(\widehat {MAN}\)
Phương pháp giải - Xem chi tiết
Tam giác cân có hai góc ở đáy bằng nhau
Tổng ba góc của 1 tam giác bằng 180 độ
Lời giải chi tiết
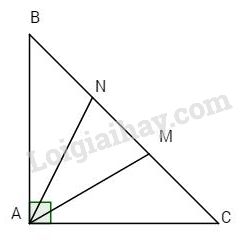
a) Ta có tam giác ABC vuông cân tại A (giả thiết)
\( \Rightarrow \widehat B = \widehat C = \dfrac{{{{180}^o} - \widehat A} }{ 2}\)\( \,= \dfrac{{{{180}^o} - {{90}^o}} }{ 2} = {45^o}\).
Lại có \(BM = AB\) (giả thiết), nên tam giác ABM cân
\( \Rightarrow \widehat {BAM} = \widehat {BMA} = \dfrac{{{{180}^o} - \widehat B} }{ 2}\)\(\, = \dfrac{{{{180}^o} - {{45}^o}} }{2} = 67,{5^o}\)
Tương tự \(\Delta CAN\) cân tại C và \(\widehat C = {45^o} \Rightarrow \widehat {CNA} = \widehat {CAN} = 67,{5^o}\)
\( \Rightarrow \widehat {AMB} = \widehat {CNA} = 67,{5^o}\).
Do đó \(\Delta AMN\) cân.
b) \(\Delta AMN\) cân tại A \( \Rightarrow \widehat {MAN} = {180^o} - \left( {\widehat {AMN} + \widehat {ANM}} \right)\)
\( = {180^o} - \left( {67,{5^o} + 67,{5^o}} \right) = {45^o}\).
Cách khác: chứng minh \(\Delta ABM = \Delta CAN\)(c.g.c) \( \Rightarrow AM = AN.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 7 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 8 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 5 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 2 - Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
